多标签分类之Principle Label Space Transformation(PLST)
文章目录
- Multi-label Classification with Principle Label Space Transformation
- Farbound Tai Hsuan-Tien Lin 台湾大学
- 2012 Neural Computation
- 摘要
- 介绍
- 超立方体视图
- 提出的方法
- 线性标签空间转换
- 原则标签空间转换
Multi-label Classification with Principle Label Space Transformation
Farbound Tai Hsuan-Tien Lin 台湾大学
2012 Neural Computation
摘要
我们提出了一种新颖的超立方体视图,它可以几何地感知多标签分类问题的标签空间。该视图不仅使我们能够统一许多现有的多标记分类方法,而且还设计了一种新颖的算法 - 原理标签空间变换(PLST),它在学习之前寻求标签之间的重要相关性。简单有效的PLST仅依赖于奇异值分解作为关键步骤。实验结果表明,PLST比传统的二元关联方法更快,并且在性能和效率方面优于流行压缩感知方法。
介绍
在这篇论文中,我们提出一个新的方法:超立方体视图,该视图将多标签分类问题中的所有可能标签集描述为高维超立方体的顶点。该视图不仅在同一框架下统一了LP,BR和LR,而且还允许我们设计更好的方法,利用这些标签集顶点的几何属性,我们通过一种新颖的方法 - 原理标签空间变换(PLST)来演示超立方体视图的使用,该方法利用高维空间中的平面捕获标签之间的重要相关性,该方法仅使用顶点的简单线性编码和简化的预测的简单线性解码,两者都可以从由标签集顶点组成的矩阵的奇异值分解(SVD)中容易地计算。此外,通过仅保持关键相关性,我们的方法可以显着减少减少任务的数量在不损失预测精度的情况下解决。
超立方体视图
超立方体视图的关键是通过向量表示标签集Y. y ∈ { 0 , 1 } K \mathbf { y } \in \{ 0,1 \} ^ { K } y∈{0,1}K,当且仅当k∈Y时,y的第k个分量为1
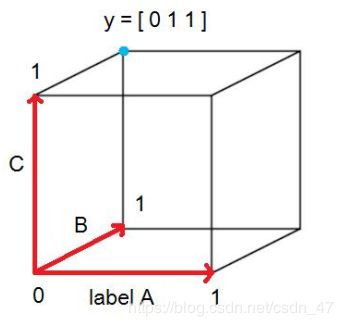
如上图所示,我们可以将每个Y可视化为K维超立方体的顶点,y的第k个分量对应于超立方体的轴,表示Y中标签k的存在或不存在,超立方体视图允许我们统一许多现有的问题转换方法
提出的方法
如上所述,CS依赖于标签集稀疏性来考虑超立方体的少量顶点。我们提出的方法源于相同的考虑,但不需要标签集稀疏性假设。从超立方体视图中,超立方体有 2 K 2^K 2K个顶点,每个训练样例 ( x n , y n ) (x_n,y_n) (xn,yn)只占一个顶点 y n y_n yn,在大型多标签分类数据集中,K通常超过数百甚至数千。然而,那么,通常训练样例数 N ≪ 2 K N \ll 2 ^ { K } N≪2K.换句话说,我们称这种现象为超立方体稀疏性,以区别于CS使用的标签集稀疏性。由于超立方体稀疏性,多标签分类算法不需要学习 R K \mathbb { R } ^ { K } RK中的整个超立方体,而是可以专注于 R K \mathbb { R } ^ { K } RK的更小的子空间。
请注意,标签集稀疏性意味着超立方体稀疏性,但反之亦然。根据定义,对于在s处具有标签集稀疏性的数据集,具有多于s个标签的所有超立方体顶点都未被训练示例占用,这就是 超立方体稀疏现象。例如,如果数据集在s = 2处是标签集稀疏的,那么这样的数据集也是超立方体稀疏的,因为占用顶点的数量最多为 ( K 2 ) + K + 1 ≪ 2 K \left( \begin{array} { c } { K } \\ { 2 } \end{array} \right) + K + 1 \ll 2 ^ { K } (K2)+K+1≪2K
另一方面,超立方体稀疏度并不一定意味着标签集稀疏性,因为少数占用的标签集顶点可能包含许多标签。例如,包含至少有 k − 1 k-1 k−1 标签集的标签集稀疏的数据集是超立方稀疏的因为这些数据占用最多 K + 1 ≪ 2 K K + 1 \ll 2 ^ { K } K+1≪2K 个顶点。
线性标签空间转换
我们现在研究一个简单的框架,侧重于子空间而不是 R K R^K RK的整个超立方体。该框架将采用M-flat作为子空间,并通过投影将超立方体的每个顶点y编码为平坦中的点h。然后,原来的多标签分类问题 { ( x n , y n ) } n = 1 N \left\{ \left( \mathbf { x } _ { n } , \mathbf { y } _ { n } \right) \right\} _ { n = 1 } ^ { N } {(xn,yn)}n=1N 成为一个多维回归问题 { ( x n , h n ) } n = 1 N \left\{ \left( \mathbf { x } _ { n } , \mathbf { h } _ { n } \right) \right\} _ { n = 1 } ^ { N } {(xn,hn)}n=1N,在获得预测 h h h 的多维回归量 r ( x ) r(x) r(x)之后,框架然后将 r ( x ) r(x) r(x)使用一些解码器D.映射回超立方体的顶点 R K \mathbb { R } ^ { K } RK。该框架将命名为线性标签空间转换(LLST),如算法中所示

可以看出,LLST将BR和CS视为特殊情况。对于BR,我们可以简单地将 P = I P = I P=I作为投影方法,并且将D作为分量方向的舍入到{0,1}函数。因为M = K,所以当K很大时需要许多回归分类器 r m r_m rm。
CS试图减少回归分类器的数量,从K个减少到M个,其投影矩阵P是从适当的分布(如Gaussian,Bernoulli或Hadamard)中随机选择的,D是CS的术语中的重建算法,需要求解每个不同x的优化问题
原则标签空间转换
由于大型多标签分类数据集中的超立方体稀疏性属性,拥有的M维的LLST算法(远小于原来的K维)在降低计算成本方面可能是有利的。我们提出的方法,原则标签空间转换(PLST),试图通过奇异值分解(SVD)找到一个投影 P P P和解码器 D D D
特别是,我们形成一个矩阵Y,每列是 y n y_n yn,即被占用的顶点。然后,我们在K×N矩阵Y上执行SVD以获得三个矩阵(Datta,1995)
Y = U Σ V T \mathbf { Y } = \mathbf { U } \boldsymbol { \Sigma } \mathbf { V } ^ { T } Y=UΣVT
这里U是K×K酉矩阵,Σ是K×N对角矩阵,V是N×N酉矩阵。通过SVD,每个 y n y_n yn可以表示为U中的奇异向量 u m u_m um的线性组合,矩阵Σ是包含对应于奇异向量um的奇异值σm的对角矩阵。
我们假设奇异值是有序的,矢量形成了穿过所有yn的平面的基础。使得 σ 1 ≥ σ 2 ≥ ⋅ ⋅ ⋅ ≥ σ K σ_1≥σ_2≥···≥σ_K σ1≥σ2≥⋅⋅⋅≥σK
上式公式可以写成:
U T Y = Σ V T \mathbf { U } ^ { T } \mathbf { Y } = \mathbf { \Sigma } \mathbf { V } ^ { T } UTY=ΣVT
其中正交基 U T U^T UT可以被视为Y的投影矩阵,其将每个y映射到不同的坐标系。由于最大M奇异值对应于原始标签空间的主要方向,我们可以丢弃 U T U^T UT中其余的奇异值及其相关的基矢量,以获得更小y的投影矩阵 P = U M T = [ u 1 u 2 ⋯ u M ] T \mathbf { P } = \mathbf { U } _ { M } ^ { T } = \left[ \begin{array} { l l l l } { \mathbf { u } _ { 1 } } & { \mathbf { u } _ { 2 } } & { \cdots } & { \mathbf { u } _ { M } } \end{array} \right] ^ { T } P=UMT=[u1u2⋯uM]T.
与CS不同其中P是随机形成的,使用主要方向的投影矩阵保证了从(训练)顶点到M-flat的最小编码误差。请注意,主要方向的概念类似于机器学习中输入预处理的主成分分析(PCA)的常用技术(Hastie等,2001)。在PCA中,通过分解由 x n x_n xn形成的矩阵来获得主要成分,并且在我们的PLST中,通过分解由 y n y_n yn形成的矩阵Y来获得主要方向。
我们现在可以为PLST定义一个有效的解码器D.因为 P = U T P = U^T P=UT是正交矩阵,所以 P − 1 = P T P^{-1} = P^T P−1=PT,这意味着 U M U_M UM可用于映射任何向量r,在平面上返回一个点 U M ⋅ r in R K \mathbf { U } _ { M } \cdot \mathbf { r } \text { in } \mathbb { R } ^ { K } UM⋅r in RK。然后,在l1距离感觉(如BR)中对最近顶点的简单舍入完成解码。
