吴恩达机器学习(Machine Learning)课程总结笔记---Week 1
文章目录
- 0. 概述
- 1. 课程大纲
- 2. 课程内容
- 2.1 引言
- (1) 什么是机器学习?
- (2) 为什么学习机器学习?
- (3) 机器学习的分类?
- a. 有监督学习
- b. 无监督学习
- c. 强化学习
- 2.2 单变量线性回归
- (1) 模型假设
- (2) 损失函数(Cost Function)
- (3) 梯度下降法
- 2.3 线性代数基础
- 3. 总结
0. 概述
吴恩达老师在Week 1课程中对机器学习进行了概括性的介绍,包括了机器学习的定义,发展和分类等。同时通过最简单的单变量线性回归,让同学们直观的了解到了机器学习的使用。
下面我们开始进入Week 1的学习。
1. 课程大纲
下图是本周课程的大纲摘要,后续小节将分解描述。
备注:下图中图片不太清晰,如需查看请前往 https://github.com/GH-SUSAN/Machine-Learning-MarkDown/tree/master/week1 下载查看。

2. 课程内容
2.1 引言
(1) 什么是机器学习?
(2) 为什么学习机器学习?
- 机器学习已经深入到生活的各个领域
- 机器学习有很好的钱途
我自己是做Android前端的,Android这几年变化极快,新的Android版本迭代,大前端技术,新的开发框架和语言层出不穷,从而使得开发门槛越来越低,需要学习的东西也越来越多。所以既然都要学习,何不学习更加前沿的技术,更加有持续性的知识,更加能够在未来沉淀下来的东西,这是我的初衷。
不知道你是什么原因,可以在blog下留言分享。
(3) 机器学习的分类?
机器学习的主流分为三大类:有监督学习,无监督学习,强化学习。
参考:https://xiaozhuanlan.com/topic/9356127804
a. 有监督学习
有监督学习可分为“回归(regression)”和“分类(Classification)”两大问题。
回归问题:预测一个连续值,即试图将输入变量和输出用一个连续函数对应起来。参考课程中的房价预测。
分类问题:预测一个离散值,即试图将输入变量与离散的类别对应起来。参考课程中的癌症恶性和良性预测。
特点:每个数据都有结果标注,。比如,一张图片是西瓜还是苹果,一套100平米的房子1000万。
b. 无监督学习
无监督学习中,并不知道有什么结果、什么结构,但可以通过聚类的方式从数据中提取一个特殊的结构,即让机器自行发现规律。
聚类:无监督学习算法是以某种方式组织数据,然后找出数据中存在的内在结构将数据进行聚类。参考课程中的DNA聚类
降维:找到更简单的方式处理复杂数据,使复杂数据看起来更简单。
特点:与有监督学习相比,其训练数据没有明确的标注。
c. 强化学习
战胜李世石的Alpha Go就是使用的强化学习,强化学习是一种学习模型,在不断的试错中找到最优结果。就像小时候你做错事,老妈给你一巴掌,你做对事,老妈给你一块糖,久而久之就知道哪些是对的,哪些是错的了。
强化学习不需要标签,你选择的行动越好,得到的反馈越多,就是要不断地尝试。比如围棋先下它3千万盘,根据输赢调整策略。
2.2 单变量线性回归
(1) 模型假设
a. 数据约定:
x ( i ) x^{(i)} x(i) -代表第i个输入变量
y ( i ) y^{(i)} y(i) -代表第i个输出变量
( x ( i ) , y ( i ) ) \left(x^{(i)}, y^{(i)}\right) (x(i),y(i))-代表第i个训练数据
( x ( i ) , y ( i ) ) ; i = 1 , … , m \left(x^{(i)}, y^{(i)}\right) ; i=1, \dots, m (x(i),y(i));i=1,…,m-代表具有m个数据的训练集
b. 学习目标:
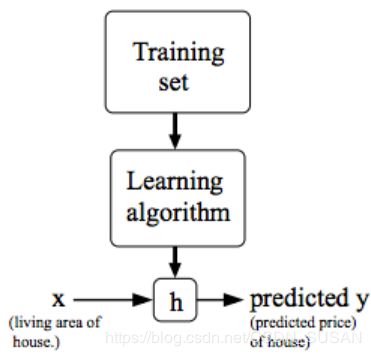
h ( x ) h(x) h(x)-假设函数, X → Y X \rightarrow Y X→Y,输入到输出的映射
通过数据拟合出一个假设函数,通过输入x能够得到输出y。
(2) 损失函数(Cost Function)
不论是机器学习何种方法,代价函数是贯穿始终的优化目标,通过优化代价函数得到最终需要的结果。
a. 直线方程假设
假设房子的大小和房价成直线关系,因此我们定义假设函数 h θ ( x ) h_{\theta}(x) hθ(x)如下所示:
h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_{0}+\theta_{1} x hθ(x)=θ0+θ1x
b. 损失数定义
如何选择 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1,使得 h θ ( x ) h_{\theta}(x) hθ(x)更接近训练集 ( X , Y ) (X, Y) (X,Y)
定义损失函数(Cost Function),表示预测值与实际值差值的平方和,除以2m,即:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ0,θ1)=2m1∑i=1m(y^(i)−y(i))2=2m1∑i=1m(hθ(x(i))−y(i))2
其中, y ^ i \hat{y}_{i} y^i= h θ ( x i ) h_{\theta}\left(x_{i}\right) hθ(xi)即对应训练数据 x ( i ) x^{(i)} x(i) 输入的预测输出。
c. 优化目标
求解$h_{\theta}(x)的问题,转化求 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 使得代价函数最小化。
min θ 0 θ 1 J ( θ 0 , θ 1 ) \min _{\theta_{0} \theta_{1}} \mathrm{J}\left(\theta_{0}, \theta_{1}\right) minθ0θ1J(θ0,θ1)
(3) 梯度下降法
关于为什么使用梯度下降法,求得 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 使损失函数最小,从而得到$h_{\theta}(x)。后面讲会有一篇专门讲解,从导数,偏导数,方向导数最后引出梯度下降。
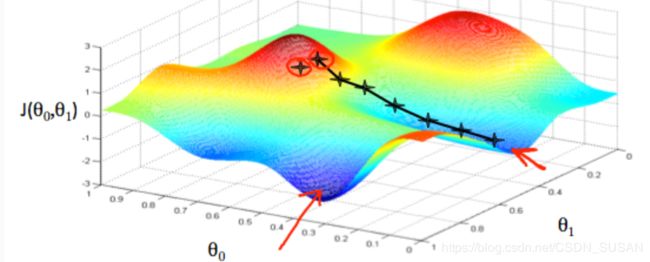
由于优化木目标是最小化损失函数 J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J(θ0,θ1),梯度下降的基本思想:
a. 基本步骤
step1 : 初始化 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 ,比如 θ 0 = 0 , θ 1 = 0 \theta_{0}=0, \theta_{1}=0 θ0=0,θ1=0
step2 : 沿着梯度下降的方向,不断修改 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 ,从而使得 J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J(θ0,θ1)不断减少,最终达到最小(全局或者局部最小)值。
temp 0 : = θ 0 − α ∗ ∂ ∂ θ 0 J ( θ 0 , θ 1 ) \operatorname{temp}0 :=\theta_{0}-\alpha * \frac{\partial}{\partial \theta_{0}} \mathrm{J}\left(\theta_{0}, \theta_{1}\right) temp0:=θ0−α∗∂θ0∂J(θ0,θ1)
temp 1 : = θ 1 − α ∗ ∂ ∂ θ 1 J ( θ 0 , θ 1 ) \operatorname{temp}1:=\theta_{1}-\alpha * \frac{\partial}{\partial \theta_{1}} \mathrm{J}\left(\theta_{0}, \theta_{1}\right) temp1:=θ1−α∗∂θ1∂J(θ0,θ1)
θ 0 : = \theta_{0} := θ0:= temp0
θ 1 : = \theta_{1} := θ1:= temp1
注意: θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 必须同步更新,不能一次仅更新其中一个。
如下图所示:
b. 学习率控制
上述过程中 α \alpha α 叫做学习率,控制柜每次更新 θ 0 , θ 1 \theta_{0,} \theta_{1} θ0,θ1 的幅度。
α \alpha α 太小:容易造成训练时间过长,收敛过慢
α \alpha α 太大:容易造成不收敛,甚至发散
如下图所示:

2.3 线性代数基础
由于训练数据庞大,特征向量维数较多,从而引入了多变量线性回归。这时候使用这种数值公式的表示,不太简洁方便,因此引入了矩阵和向量来定义 h θ ( x ) h_{\theta}(x) hθ(x) 和 J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J(θ0,θ1)。
X ( i ) = [ x 0 ( i ) x 1 ( i ) x 2 ( i ) ⋯ x j ( i ) ] X^{(i)}=\left[ \begin{array}{l}{x_{0}^{(i)}} \\ {x_{1}^{(i)}} \\ {x_{2}^{(i)}} \\ {\cdots} \\ {x_{j}^{(i)}}\end{array}\right] X(i)=⎣⎢⎢⎢⎢⎢⎡x0(i)x1(i)x2(i)⋯xj(i)⎦⎥⎥⎥⎥⎥⎤-表示第i个输入变量,有j维度,默认 x 0 ( i ) x_{0}^{(i)} x0(i)=1
θ = [ θ 0 θ 1 ⋯ θ j ] \theta=\left[ \begin{array}{l}{\theta_{0}} \\ {\theta_{1}} \\ {\cdots} \\ {\theta_{j}}\end{array}\right] θ=⎣⎢⎢⎡θ0θ1⋯θj⎦⎥⎥⎤-参数 θ \theta θ
h θ ( x ) = θ 0 + θ 1 x 1 + … + θ j x j = θ T X h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\ldots+\theta_{j} x_{j}=\theta^{T} X hθ(x)=θ0+θ1x1+…+θjxj=θTX
这样就简洁的定义了多变量线性回归的 h θ ( x ) h_{\theta}(x) hθ(x)
关于线性代数的基础知识,将单独用一篇博客来总结。
3. 总结
以上就是本周的全部知识,我理解难点在于梯度下降这块,对梯度和偏导数不太熟悉的同学,请就相关知识点补充。
千里之行始于足下,加油!