吴恩达机器学习(Machine Learning)课程总结笔记---Week 2
文章目录
- 0 概述
- 1. 课程大纲
- 2. 课程内容
- 2.1 多元线性回归
- 2.2 多元线性回归的梯度下降
- 2.3 特征缩放
- 2.4 学习率
- 2.5 构造特征以及多项式回归
- 2.6 正规方程法
- 2.6.1 正规方程的推导
- 2.6.2 可逆性分析
- 2.6.3 梯度下降和正规方程的比较
- 2.7 Octave 简明教程
- 3. 课后编程作业
- 4. 总结
0 概述
在week 1中,我们学习了单变量线性回归,但现实世界往往不是简单的一元函数就能够表示的,因此基于Week 1的基础上,Week 2 将对多变量线性回归,进行深入的讲解。
并且通过调整学习率,特征缩放,特征构造,均值归一化,来使我们更好地进行迭代回归。
1. 课程大纲
2. 课程内容
2.1 多元线性回归
在week 1中我们通过假设模型 h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_{0}+\theta_{1} x hθ(x)=θ0+θ1x去预测房价和面积之间的关系。但实际生活中房价不仅仅与面积有关,与新旧等多个因素相关,如下图所示:

决定房价的因素,从单变量变成了一个向量。
x = [ x 0 x 1 x 2 . . . x n ] x=\left[ \begin{array}{c}{x_{0}} \\ {x_{1}} \\ {x_{2}}\\... \\ {x_{n}}\end{array}\right] x=⎣⎢⎢⎢⎢⎡x0x1x2...xn⎦⎥⎥⎥⎥⎤
因此,假设模型就定义为:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
这就是多变量线性回归。
注:这里需要说一下,什么样的函数可以被称为线性函数?
当函数满足以下两个性质,就被称为线性函数
齐次性: f ( a x ) = a f ( x ) f(a x)=a f(x) f(ax)=af(x)
可加性: f ( x + y ) = f ( x ) + f ( y ) f(x+y)=f(x)+f(y) f(x+y)=f(x)+f(y)
2.2 多元线性回归的梯度下降
假设函数:
h θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_{\theta}(x)=\theta^{T} x=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} hθ(x)=θTx=θ0x0+θ1x1+θ2x2+⋯+θnxn
损失函数:
J ( θ 0 , θ 1 , … , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ0,θ1,…,θn)=2m1∑i=1m(hθ(x(i))−y(i))2
其中, x ( i ) x^{(i)} x(i)第i个训练数据的输入变量,现在是一个向量。
优化目标:
min θ ⃗ J ( θ 0 , θ 1 , ⋯ , θ n ) \min _{\vec{\theta}} \mathrm{J}\left(\theta_{0}, \theta_{1},\cdots, \theta_{n}\right) minθJ(θ0,θ1,⋯,θn)
迭代步骤:
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , … , θ n ) \theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \ldots, \theta_{n}\right) θj:=θj−α∂θj∂J(θ0,…,θn)= θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
直到收敛(一般我们认为一次迭代 J ( θ 0 , θ 1 , ⋯ , θ n ) {J}\left(\theta_{0}, \theta_{1},\cdots, \theta_{n}\right) J(θ0,θ1,⋯,θn)小于一个数值,比如10^-3,就可以认为收敛了)。
注意:所有参数都要以同个costFunction当前参数来进行运算更新(不能更新一个 θ j \theta_{j} θj替换一个),最后替换生成新的costFunction。
2.3 特征缩放
从2.1节中的房价表,可以发现面积、房间数、年限都不在一个数量级上,这样会导致 θ i \theta_{i} θi的数值也不能在一个数量级,最终导致不能够简单快速的收敛。
因此,提出了特征缩放来解决这个问题。
特征缩放:将所有的特征变量压缩到大致为[-1, 1]的范围。
比如:
x i = x i s i x_{i}=\frac{x_{i}}{s_{i}} xi=sixi 其中, s i s_{i} si是最大值-最小值,这样就缩放到[0-1]范围。
或者采用均值归一化,
x i = x i − μ i s i x_{i}=\frac{x_{i}-\mu_{i}}{s_{i}} xi=sixi−μi, 其中, μ i \mu_{i} μi是 X X X向量元素的平均值, s i s_{i} si是最大值-最小值或者可以用标准偏差。
通过特征缩放,能够使得训练过程更加有效的收敛。
2.4 学习率
每一次迭代更新 θ \theta θ,都会用到 α \alpha α,它被称为学习率。一般情况下:
α \alpha α过小:收敛速度过慢
α \alpha α过大:不能收敛,甚至可能发散,有时候也会出现收敛过慢。
一般 α \alpha α可以从 0.001,0.003,0.01,0.03,0.1,0.3,1 这几个值去尝试,选一个最优的。
2.5 构造特征以及多项式回归
到目前为止,我们仅仅通过图表知道房价和面积,年代,房间数…特征有关系,但是并不明确知道为什么会是这些特征,是否还有其他特征。往往如果这些简单的特征无法正确表达房价,是否能够尝试构造一个特征呢?
答案是肯定的。
比如构造特征 x 1 / x 2 x_{1} / x_{2} x1/x2,表示房间总面积除以房间数,表征每个房间的平均面积,作为新的特征,或者对面积进行开方的到新的特征。
h θ ( x ) = θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) h_{\theta}(x)=\theta_{0}+\theta_{1}(s i z e)+\theta_{2} \sqrt{(s i z e)} hθ(x)=θ0+θ1(size)+θ2(size)
关于如何去选取和构造特征:这只能通过观察和推测了,需要在相关领域有足够的经验。在机器学习中,有专门的特征工程,就是为了能够找到比较好的feature。
2.6 正规方程法
2.6.1 正规方程的推导
在初中的时候,学习解方程组,老师常说:有几个方程就能解出几个变量,其实那就是正规方程的开端。然而真实情况并非如此,这里必须有一个前提,所有的方程的系数是线性无关的。
现在引入的正规方程,同样是根据初中时候的思想,不用不断迭代,一次就能够求解出最优的 θ \theta θ。
如下图所示,我们引入 x 0 x_{0} x0列,作为 θ 0 \theta_{0} θ0,也就是偏移量固定系数。

对于矩阵 X X X的每一行,相当于一个训练数据的输入变量,记为 x ( i ) x^{(i)} x(i),
x ( i ) = [ x 0 ( i ) x 1 ( i ) ⋮ x n ( i ) ] x^{(i)}=\left[ \begin{array}{c}{x_{0}^{(i)}} \\ {x_{1}^{(i)}} \\ {\vdots} \\ {x_{n}^{(i)}}\end{array}\right] x(i)=⎣⎢⎢⎢⎢⎡x0(i)x1(i)⋮xn(i)⎦⎥⎥⎥⎥⎤,其中i表示第i个训练数据, i ∈ [ 1 , m ] i \in[1, m] i∈[1,m]; n n n表示输入变量 x ( i ) x^{(i)} x(i)第 n n n个特征; x ( i ) x^{(i)} x(i)有n+1维。
因此可以将矩阵 X X X表示为:
X = [ ( x ( 1 ) ) T ( x ( 2 ) ) T ⋮ ( x ( m ) ) T ] X=\left[ \begin{array}{c}{(x^{(1)}})^{T} \\ ({x^{(2)}})^{T} \\ {\vdots} \\ {(x^{(m)})^{T}}\end{array}\right] X=⎣⎢⎢⎢⎡(x(1))T(x(2))T⋮(x(m))T⎦⎥⎥⎥⎤,可以看到矩阵 X X X是 m ∗ ( n + 1 ) m*(n+1) m∗(n+1)维的。
可以将向量 θ \theta θ表示为:
Θ = [ θ 0 θ 1 ⋮ θ n ] \Theta=\left[ \begin{array}{c}{\theta_{0}} \\ {\theta_{1}} \\ {\vdots} \\ {\theta_{n}}\end{array}\right] Θ=⎣⎢⎢⎢⎡θ0θ1⋮θn⎦⎥⎥⎥⎤
可以将输出向量 Y Y Y表示为:
Y = [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ] Y=\left[ \begin{array}{c}{y^{(1)}} \\ {y^{(2)}} \\ {\vdots} \\ {y^{(m)}}\end{array}\right] Y=⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤
综上可以得到正规方程组:
假设模型:
h Θ ( X ) = X ∗ Θ h_{\Theta}(X)=X*\Theta hΘ(X)=X∗Θ
损失函数:
F ( Θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \mathrm{F}(\Theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} F(Θ)=2m1∑i=1m(hθ(x(i))−y(i))2,用矩阵 X X X和向量 Θ \Theta Θ, Y Y Y,简化损失函数,
X ⋅ Θ − Y = [ ( x ( 1 ) ) T ⋮ ( x ( m ) ) T ] ⋅ [ θ 0 θ 1 ⋮ θ n ] − [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ] = [ h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) ⋮ h θ ( x ( m ) ) − y ( m ) ] X \cdot \Theta-Y=\left[ \begin{array}{c}\\ {\left(x^{(1)}\right)^{T}} \\ {\vdots} \\ {\left(x^{(m)}\right)^{T}}\end{array}\right] \cdot \left[ \begin{array}{c}{\theta_{0}} \\ {\theta_{1}} \\ {\vdots} \\ {\theta_{n}}\end{array}\right]-\left[ \begin{array}{c}{y^{(1)}} \\ {y^{(2)}} \\ {\vdots} \\ {y^{(m)}}\end{array}\right]=\left[ \begin{array}{c}{h_{\theta}\left(x^{(1)}\right)-y^{(1)}} \\ {h_{\theta}\left(x^{(2)}\right)-y^{(2)}} \\ {\vdots} \\ {h_{\theta}\left(x^{(m)}\right)-y^{(m)}}\end{array}\right] X⋅Θ−Y=⎣⎢⎢⎡(x(1))T⋮(x(m))T⎦⎥⎥⎤⋅⎣⎢⎢⎢⎡θ0θ1⋮θn⎦⎥⎥⎥⎤−⎣⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡hθ(x(1))−y(1)hθ(x(2))−y(2)⋮hθ(x(m))−y(m)⎦⎥⎥⎥⎤
因此,可简化损失函数为:
F ( Θ ) = 1 2 m ( X ⋅ Θ − Y ) T ( X ⋅ Θ − Y ) \mathrm{F}(\Theta)=\frac{1}{2 m}(X \cdot \Theta-Y)^{T}(X \cdot \Theta-Y) F(Θ)=2m1(X⋅Θ−Y)T(X⋅Θ−Y)
这就是矩阵和向量优雅的表示。
经过推到,可得结论:
Θ = ( X T X ) − 1 X T Y \Theta=\left(X^{T} X\right)^{-1} X^{T} Y Θ=(XTX)−1XTY
其中前提条件是 X T X X^{T}X XTX 是非奇异(非退化)矩阵, 即 ∣ X T X ∣ ! = 0 \left|X^{T} X\right| != 0 ∣∣XTX∣∣!=0
2.6.2 可逆性分析
求解 Θ = ( X T X ) − 1 X T Y \Theta=\left(X^{T} X\right)^{-1} X^{T} Y Θ=(XTX)−1XTY,需要求解 X T X X^{T} X XTX的逆。
一般出现不可逆有两种情况:
(1) 列向量线性相关,即训练集中存在冗余特征,此时应该剔除掉多余特征;
(2) 特征过多,此时应该去掉影响较小的特征,或使用“正则化”;当样本总数 m 小于等于特征数量 n 时, X T X X^{T}X XTX 一定不可逆。
正则化处理:
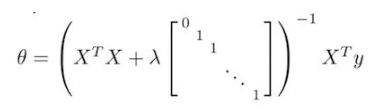
当 λ > 0 \lambda>0 λ>0时,可以保证矩阵可逆。
在octave中有两个方法,一个pinv()求解伪逆矩阵,一个inv()求解逆矩阵,我们通常使用pinv()来求解,因为即使矩阵不可逆,也依然能计算得结果。
2.6.3 梯度下降和正规方程的比较
梯度下降法,
优点:梯度下降在超大数据集的训练中,表现依然良好;适用于各种模型。
缺点:需要选择学习率 α \alpha α,需要很多次迭代计算才能收敛
正规方程法,
优点:不用多次迭代,不用选择学习率 α \alpha α
缺点:需要计算 X T X X^{T}X XTX,且其时间复杂度为 O ( n 3 ) O\left(n^{3}\right) O(n3),一般情况下,当n>10000的时候,就不考虑使用正规方程了;无法计算Logistic Regression 的classification问题
2.7 Octave 简明教程
本课程所有的代码,都是使用octave完成的,octave可以理解为对Matlab的GUN免费版,基本的语法都和Matlab一致。当然如果你有盗版的Matlab,也可以直接使用。不过由于语法的些许不同,可能会耽误调试和提交代码,Octave同样很好用建议直接下载使用。
Octave教程内容较多,可以参考我总结的一篇《Octave/Matlab 简明教程》,内容很详细:
https://blog.csdn.net/CSDN_SUSAN/article/details/90266610
3. 课后编程作业
我将课后编程作业的参考答案上传到了github上,包括了octave版本和python版本,大家可参考使用。
github地址:https://github.com/GH-SUSAN/Machine-Learning-MarkDown/tree/master/week2
4. 总结
多变量线性回归以及多项式回归,让我们进一步的对复杂的回归问题有了了解。
同时学习工具octave也可以帮助我们快速的完成编码实现回归的工作。
在以后的工作中,octave会成为有力的工具,因为它能够快速实现你的想法,当你实现了这些想法并发现有效后,再用java或者c或者python做进一步部署,这将是一个很好的工作思路。