POJ1976和POJ3624《01背包,动态规划》详细讲解,acm新手快来看看
poj1976和poj3624《动态规划,01背包》经典类型 详细讲解
上次写的匈牙利算法可能比较难,这次给大家来一个比较简单的动态规划吧
动态规划的类型有很多种,这次挑个最简单的——01背包(作为acm的萌新,我也只学会了这个。。)。所谓01背包就是对于一个东西,只有两种状态,拿还有不拿,这类题目都算是01背包。最经典的就是给一个固定容量的背包,然后给一堆有体积和价值的物品,问怎么装能拿走最大价值。
poj3624
下面上题:poj3624原题
Charm Bracelet
Bessie has gone to the mall’s jewelry store and spies a charm bracelet. Of course, she’d like to fill it with the best charms possible from the N (1 ≤ N ≤ 3,402) available charms. Each charm i in the supplied list has a weight Wi (1 ≤ Wi ≤ 400), a ‘desirability’ factor Di (1 ≤ Di ≤ 100), and can be used at most once. Bessie can only support a charm bracelet whose weight is no more than M (1 ≤ M ≤ 12,880).
Given that weight limit as a constraint and a list of the charms with their weights and desirability rating, deduce the maximum possible sum of ratings.
Input
Line 1: Two space-separated integers: N and M
Lines 2..N+1: Line i+1 describes charm i with two space-separated integers: Wi and Di
Output
Line 1: A single integer that is the greatest sum of charm desirabilities that can be achieved given the weight constrsints
Sample Input
4 6
1 4
2 6
3 12
2 7
Sample Output
23
题意比较简单,某个人想用珠宝提高自己的吸引力什么的,最大能承受M重量,给N个物品的重量和价值,求最大价值。
对于第i个物品,它可以拿走或者不拿走,也就是一共有2的n方种选择,怎么体现这2的n方种选择呢?就是用动态规划了,因为是求最大值,得转移方程 dp[j]=max(dp[j-wi]+Di , dp[j])
下标j表示背包容量,dp[j]表示j容量的背包取到第i件物品能拿到的最大值,下面是代码
#includescanf("%d%d",&wi[i],&di[i]);
}
memset(dp,0,sizeof(dp)); //清零
/*for(int i=0;i=wi[i];j--)
{
dp[j]=max(dp[j],dp[j-wi[i]]+di[i]);
}
}
printf("%d\n",dp[m]);*/
//上面注释的这种也可以ac,不过两个dp含义有点区别,下面是恰好达到重量为j的最大价值,上面是在重量小于等于j的最大价值,即不一定装满。
//用下面这种要注意不能输出dp[m],因为他不一定装满背包。
int maxn=0;
for(int i=0;ifor(int j=m;j>=wi[i];j--)
{
if(j==wi[i]||dp[j-wi[i]])
{
dp[j]=max(dp[j],dp[j-wi[i]]+di[i]);
maxn=max(maxn,dp[j]);
}
}
}
printf("%d",maxn);
return 0;
} poj1976
上面这种是比较经典的01背包,下面这种也是01背包,不过不是向上面的那么明显。
poj1976
A train has a locomotive that pulls the train with its many passenger coaches. If the locomotive breaks down, there is no way to pull the train. Therefore, the office of railroads decided to distribute three mini locomotives to each station. A mini locomotive can pull only a few passenger coaches. If a locomotive breaks down, three mini locomotives cannot pull all passenger coaches. So, the office of railroads made a decision as follows:
1. Set the number of maximum passenger coaches a mini locomotive can pull, and a mini locomotive will not pull over the number. The number is same for all three locomotives.
2. With three mini locomotives, let them transport the maximum number of passengers to destination. The office already knew the number of passengers in each passenger coach, and no passengers are allowed to move between coaches.
3. Each mini locomotive pulls consecutive passenger coaches. Right after the locomotive, passenger coaches have numbers starting from 1.
For example, assume there are 7 passenger coaches, and one mini locomotive can pull a maximum of 2 passenger coaches. The number of passengers in the passenger coaches, in order from 1 to 7, is 35, 40, 50, 10, 30, 45, and 60.
If three mini locomotives pull passenger coaches 1-2, 3-4, and 6-7, they can transport 240 passengers. In this example, three mini locomotives cannot transport more than 240 passengers.
Given the number of passenger coaches, the number of passengers in each passenger coach, and the maximum number of passenger coaches which can be pulled by a mini locomotive, write a program to find the maximum number of passengers which can be transported by the three mini locomotives.
Input
The first line of the input contains a single integer t (1 <= t <= 11), the number of test cases, followed by the input data for each test case. The input for each test case will be as follows:
The first line of the input file contains the number of passenger coaches, which will not exceed 50,000. The second line contains a list of space separated integers giving the number of passengers in each coach, such that the ith number of in this line is the number of passengers in coach i. No coach holds more than 100 passengers. The third line contains the maximum number of passenger coaches which can be pulled by a single mini locomotive. This number will not exceed 1/3 of the number of passenger coaches.
Output
There should be one line per test case, containing the maximum number of passengers which can be transported by the three mini locomotives.
Sample Input
1
7
35 40 50 10 30 45 60
2
Sample Output
240
题意就是有辆列车break down了,派出3个列车头去把列车拉回来,但是每个列车头只能拉动m节车厢(车厢要连续的)给出每节车厢的人数,问最多能拉多少人回来。题目有给出m小于列车节数的1/3,所以每个车头都要拉m节才能最大。
 转移方程
转移方程
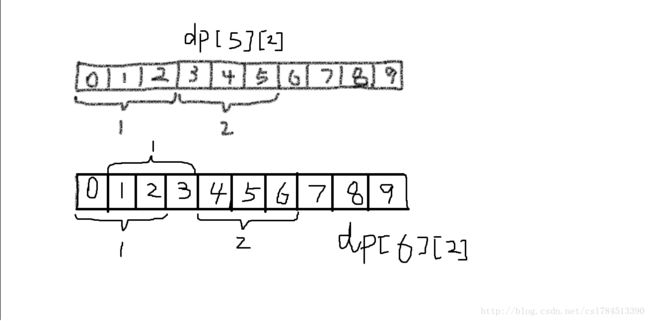
dp[i][j]=max(dp[i-1][j],dp[i-m][j-1]+vv[i])其中i表示扫描到第i节车厢,j是用几个火车头。如上图,假设m为3,列车有10节。dp[5][2]已经求出,那么dp[6][2]有三种可能,
不取6号车厢,那dp[6][2]=dp[5][2],或者不取0号或者3号车厢,到底取0号还是3号,在dp[4][1]已经求出,所以dp[6][2]=dp[4][1]+vv[6]。比较两个式子取最大即可。
#includescanf("%d",&num[i]);
}
int m;
scanf("%d",&m);
for(int i=0;ifor(int j=i;j>=0&&j>i-m;j--)
{
vv[i]+=num[j]; //即使不够m节也是一个车头就拉完,所以不需要i>m
}
}
memset(dp,0,sizeof(dp));
int k;
for(int i=0;ifor(int j=1;j<4;j++)
{
if(i-m<0)
k=0;
else
k=i-m;
dp[i][j]=max(dp[i-1][j],dp[k][j-1]+vv[i]);
}
}
printf("%d\n",dp[n-1][3]); //标号是从0~n-1
}
return 0;
} 这次是第二次写博客,这个markdown编辑器功能挺好用,就是不知道为什么换行或者插入图片或者代码总是会把上文打乱,心好烦,哪位大佬若是知道请留言告诉我!
acm队萌新入坑还不久,若是大家有什么建议或者什么好的算法亦或是找到什么bug,欢迎留言!!!