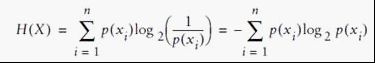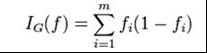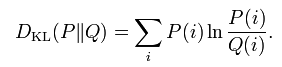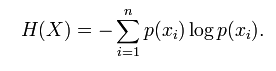《集体智慧编程》之决策树（学习笔记）

原理：

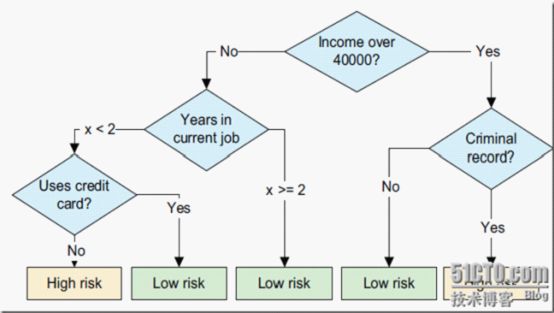
决策树提供了一种展示类似在什么条件下会得到什么值这类规则的方法。比如，在贷款申请中，要对申请的风险大小做出判断，图是为了解决这个问题而建立的一棵决策树，从中我们可以看到决策树的基本组成部分：决策节点、分支和叶子。决策树中最上面的节点称为根节点，是整个决策树的开始。本例中根节点是“收入>￥40,000”，对此问题的不同回答产生了“是”和“否”两个分支。（百度百科） 

以上图片来自（http://hadstj.blog.51cto.com/blog/653879/600478）

混杂程度的测度，有几种不同的度量方式可供选择，此处我们将考察其中的两种：基尼不纯度（Giniimpurity）和熵（entropy）

熵（entropy）：

熵（entropy）指的是体系的混乱的程度，当我们尝试把混合集合A={B1,B2,C1,C2…..} （其中Bx表示一个类别的元素，Cx表示另外一个） 划分为2个集合 M、N（即决策树的2个分支时候），比较好的划分是 M 里面都是 Bx，N里面都是Cx，这时候我们需要一个函数对 划分以后 的 集合进行评估，看看是否纯度 够“纯”。如果很纯，很有序，熵就是0.

理解该公式：p(xi) 越平均，系统约混乱，如果系统只有2个元素x1、x2，x1出现概率是0.5，x2出现概率也是0.5，即p(x1) =0.5  p(x2) =0.5 ，这时公式计算结果为1； p(xi)如果比较不平均，比如p(x2) =1，那就是系统很确定，一点都不混乱，肯定是x2构成，这时熵计算结果就是0.

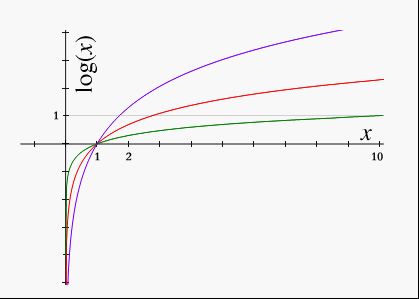
　　这个规律刚刚好是 log 函数特点 过（1，0）这个点（见下图），我想这个就是克劳德·艾尔伍德·香农设计这个公式选择log函数的道理。

基尼不纯度（Giniimpurity）：

公式如下：

公式基本上也符合以上熵的 规律： 集合越纯  值越小，如果只有2个元素时候，每个元素出现概率就是0.5，这时 I = 0.5*0.5 +0.5*0.5 =0.5
    0.5*0.5   # 我的理解是  K1（出现概率0.5） 被当做 其他Kx的概率（出现概率0.5）

熵和基尼不纯度之间的主要区别在于，熵达到峰值的过程要相对慢一些，因此，熵对于混乱集合的“判罚”往往要更重一些。

信息增益（Kullback–Leibler divergence）：

设离散随机变量的概率分布P和Q，它们的信息增益定义为 

其中分布P和Q必须是概率分布，而且对于任何P(i)>0，必须有Q(i)>0。当P(i)=0时，公式的值为0。从公式看，信息增益是以分布P为权重的P和Q对数差值的加权平均。信息增益的连续分布形式：

其中p和q表示P和Q的密度概率函数

特征选择：

在信息增益中，衡量标准是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。对一个特征而言，系统有它和没它时信息量将发生变化，而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量，就是熵。假如有变量X，其可能的取值有n种，每一种取到的概率为Pi，那么X的熵就定义为 

也就是说X可能的变化越多，X所携带的信息量越大，熵也就越大。对于文本分类或聚类而言，就是说文档属于哪个类别的变化越多，类别的信息量就越大。所以特征T给聚类C或分类C带来的信息增益为IG(T)=H(C)-H(C|T)。 H(C|T)包含两种情况：一种是特征T出现，标记为t，一种是特征T不出现，标记为t'。所以H(C|T)=P(t)H(C|t)+P(t')H(C|t)，再由熵的计算公式便可推得特征与类别的信息增益公式。

信息增益最大的问题在于它只能考察特征对整个系统的贡献，而不能具体到某个类别上，这就使得它只适合用来做所谓“全局”的特征选择（指所有的类都使用相同的特征集合），而无法做“本地”的特征选择（每个类别有自己的特征集合，因为有的词，对这个类别很有区分度，对另一个类别则无足轻重）。

决策树过度拟合（overfitted）：

为了防止决策树过度拟合（overfitted），因为前述算法直到无法进一步降低熵的时候才会停止分支的创建过程，所以一种可能的解决办法是，只要当熵减少的数量小于某个最小值时，我们就停止分支的创建，这种策略时常被人使用，但是它有一个小小的缺陷：我们有可能遇到这样的数据集，某次分支的创建并不会令熵降低多少，但是随后创建的分支却会使熵大幅降低，对此，一种替代策略是，先构造好如前所述的整棵树，然后再尝试消除多余的节点，这个过程就是剪枝。代码中prune（）函数即是实现此功能。

缺失数据的处理：

如果缺失某些数据，而这些数据是确定分支走向所必须的，那么实际上我们可以选择两个分支都走，我们是对各个分支进行加权统计，在一个基本的决策树中，所有的节点都隐含有一个值为1的权重，即观测数据对于数据项是否属于某个特定分类的概率具有百分百的影响。而如果要走多个分支的话，那么我们可以给每个分支赋予一个权重，其值等于所有位于该分支的其他数据行所占的比重。代码中mdclassify（）函数即是实现此功能。

Python代码如下：

# This Python file uses the following encoding: utf-8
my_data = [['slashdot','USA','yes',18,'None'],
           ['google','France','yes',23,'Premium'],
           ['digg','USA','yes',24,'Basic'],
           ['kewitobes','France','yes',23,'Basic'],
           ['google','UK','no',21,'Premium'],
           ['(direct)','New Zealand','no',12,'None'],
           ['(direct)','UK','no',21,'Basic'],
           ['google','USA','no',24,'Premium'],
           ['slashdot','France','yes',19,'None'],
           ['digg','USA','no',18,'None'],
           ['google','UK','no',18,'None'],
           ['kiwitobes','UK','no',19,'None'],
           ['digg','New Zealand','yes',12,'Basic'],
           ['google','UK','yes',18,'Basic'],
           ['kiwitobes','France','yes',19,'Basic']]

class decisionnode:
    def __init__(self,col=-1,value=None,results=None,tb=None,fb=None):
        self.col = col             #待检验的判断条件（the criteria to be tested）所对应的列索引值
        self.value = value         #为了使结果为true，当前列必须匹配的值  
        self.results = results     #保存针对当前分支的结果，是一个字典，除叶节点外，其他节点上该值都为None
        #tb和fb也是decisionnode，对应结果分别是true或false时，树上相对于当前节点的子树上的节点
        self.tb = tb               
        self.fb = fb

#在某一列上对数据集合进行拆分，能够处理数值型数据或名词性数据
def divideset(rows,column,value):
    #定义一个函数，令其告诉我们数据行属于第一组（返回值为true）还是第二组（返回值为false)
    split_function = None
    if isinstance(value,int) or isinstance(value,float):
        split_function = lambda row:row[column] >= value
    else:
        split_function = lambda row:row[column] == value
    
    #将数据集拆分成两个集合，并返回
    set1 = [row for row in rows if split_function(row)]
    set2 = [row for row in rows if not split_function(row)]
    return (set1,set2)

#对各种可能结果进行计数（每一行数据的最后一列记录了这一计数结果）
def uniquecounts(rows):
    results = {}
    for row in rows:
        #计数结果在最后一列   
        r = row[len(row)-1]
        if r not in results:
            results[r] = 0
        results[r] += 1
    return results

#随机放置的数据项出现于错误分类中的概率
def giniimpurity(rows):
    total = len(rows)
    counts = uniquecounts(rows)
    imp = 0
    for k1 in counts:
        p1 = float(counts[k1])/total
        for k2 in counts:
            if k1 == k2: continue
            p2 = float(counts[k2])/total
            imp += p1*p2
    return imp

#熵是遍历所有可能结果之后所得到的p(x)log(p(x))之和
def entropy(rows):
    from math import log
    log2 = lambda x:log(x)/log(2)
    results = uniquecounts(rows)
    #此处开始计算熵的值  
    ent = 0.0
    for r in results.keys():
        p = float(results[r])/len(rows)
        ent = ent - p*log2(p)
    return ent
        
def buildtree(rows,scoref=entropy):
    if len(rows) == 0:
        return decisionnode()
    current_score = scoref(rows)
    
    #定义一些变量以记录最佳拆分条件
    best_gain = 0.0
    best_criteria = None
    best_sets = None
    
    column_count = len(rows[0])-1
    for col in range(0,column_count):
        #在当前列中生成一个由不同值构成的序列
        column_values={}
        for row in rows:
            column_values[row[col]] = 1
        #接下来根据这一列中的每一个值，尝试对数据进行拆分
        for value in column_values.keys():
            (set1,set2) = divideset(rows,col,value)  
            
            #信息增益
            p = float(len(set1))/len(rows)   
            gain = current_score - p*scoref(set1) - (1-p)*scoref(set2)
            if gain > best_gain and len(set1) > 0 and len(set2) > 0:
                best_gain = gain
                best_criteria = (col,value)
                best_sets = (set1,set2)
    #创建子分支
    if best_gain > 0:
        trueBranch = buildtree(best_sets[0])
        falseBranch = buildtree(best_sets[1])
        return decisionnode(col=best_criteria[0],value=best_criteria[1],
                           tb=trueBranch,fb=falseBranch)  
    else:
        return decisionnode(results=uniquecounts(rows))                                 
    
def classify(observation,tree):
    if tree.results != None:
        return tree.results
    else:
        v = observation[tree.col]
        branch = None
        if isinstance(v,int) or isinstance(v,float):
            if v >= tree.value: branch = tree.tb
            else: branch = tree.fb
        else:
            if v == tree.value: 
                branch = tree.tb
            else: branch = tree.fb
        return classify(observation,branch)
def mdclassify(observation,tree):
    if tree.results != None:
        return tree.results
    else:
        v = observation[tree.col]
        if v == None:
            tr,fr = mdclassify(observation,tree.tb),mdclassify(observation,tree.fb)
            tcount = sum(tr.values())
            fcount = sum(fr.values())
            tw = float(tcount)/(tcount+fcount)
            fw = float(fcount)/(tcount+fcount)
            result = {}
            for k,v in tr.items(): result[k] = v*tw
            for k,v in fr.items():
                if k not in result: result[k] = 0
                result[k] += v*fw
            return result
        else:
            if isinstance(v,int) or isinstance(v,float):
                if v >= tree.value: branch = tree.tb
                else: branch = tree.fb
            else:
                if v == tree.value: branch = tree.tb
                else: branch = tree.fb
        return mdclassify(observation,branch)
            
    
def printtree(tree,indent=' '):
    #这是一个叶节点吗？
    if tree.results != None:
        print(str(tree.results))
    else:
        #打印判断条件        
        print(str(tree.col)+':'+str(tree.value)+'?')
        #打印分支 
        print(indent+'T—>',end='')
        printtree(tree.tb,indent+' ')     
        print(indent+'F—>',end='')
        printtree(tree.fb,indent+' ')

def prune(tree,mingain):
    #如果分支不是叶节点，则对其进行剪枝操作
    if tree.tb.results == None:
        prune(tree.tb,mingain)
    if tree.fb.results == None:
        prune(tree.fb,mingain)
    
    #如果两个分支都是叶节点，则判断他们是否须要合并
    if tree.tb.results != None and tree.fb.results != None:
        #构造合并后的数据集
        tb,fb=[],[]
        for v,c in tree.tb.results.items():
            tb += [[v]]*c
        for v,c in tree.fb.results.items():
            fb += [[v]]*c 
            
        #检查熵的减少情况
        delta = entropy(tb+fb) - (entropy(tb) + entropy(fb)/2)
        if delta < mingain:
            #合并分支
            tree.tb,tree.fb = None,None
            tree.results = uniquecounts(tb + fb)
                    
            

#print(dividest(my_data,2,'yes'))
#print(giniimpurity(my_data))
#print(entropy(my_data))
#set1,set2 = divideset(my_data,2,'yes')
#print(entropy(set1))
#print(giniimpurity(set1))
tree = buildtree(my_data)
#prune(tree,0.1)
#print(printtree(tree))
#prune(tree,1.0)
#print(printtree(tree))
print(mdclassify(['google','France',None,None],tree))