Python实现蒙特卡罗方法
一、蒙特卡罗方法简介
蒙特卡罗(Monte Carlo)方法:简单来说,蒙特卡洛的基本原理简单描述是先大量模拟,然后计算一个事件发生的次数,再通过这个发生次数除以总模拟次数,得到想要的结果,精髓就是:用统计结果去计算频率,从而得到真实值的近似值。蒙特卡洛方法可以应用在很多场合,但求的是近似解,在模拟样本数越大的情况下,越接近与真实值,但样本数增加会带来计算量的大幅上升。
二、实例
1.求圆周率pi的近似值:
(1)正方形内部有一个相切的圆,它们的面积之比是π/4。现在,在这个正方形内部,随机产生10000个点,计算它们与中心点的距离,从而判断是否落在圆的内部,若这些点均匀分布,则圆周率 pi=res/n p i = r e s / n 。
其中res:表示落到圆内投点数 n:表示总的投点数
(2)代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
# 投点次数
n = 10000
# 圆的半径、圆心
r = 1.0
a,b = (0.,0.)
# 正方形区域
x_min, x_max = a-r, a+r
y_min, y_max = b-r, b+r
# 在正方形区域内随机投点
x = np.random.uniform(x_min, x_max, n) #均匀分布
y = np.random.uniform(y_min, y_max, n)
#计算点到圆心的距离
d = np.sqrt((x-a)**2 + (y-b)**2)
#统计落在圆内点的数目
res = sum(np.where(d < r, 1, 0))
#计算pi的近似值(Monte Carlo:用统计值去近似真实值)
pi = 4 * res / n
print('pi: ',pi)
#画个图
fig = plt.figure()
axes = fig.add_subplot(111)
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') #防止图像变形
circle = Circle(xy=(a,b), radius=r ,alpha=0.5)
axes.add_patch(circle)
plt.show()(3)运行结果:

pi的值是:
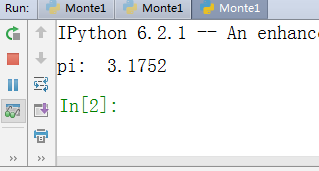
可以看出存在一定误差,模拟样本越大,误差也会随之减小。
2.求定积分的近似值
(1)在一个1×1的正方形区域里,使用蒙特卡洛方法,随机在这个正方形里面产生大量随机点(数量为n),计算有多少点(数量为res)落在函数下方区域内,res/n就是所要求的积分值,也即红色区域的面积。
(2)代码
n = 30000
#矩形边界区域
x_min, x_max = 0.0, 1.0
y_min, y_max = 0.0, 1.0
#在矩形区域内随机投点x
x = np.random.uniform(x_min, x_max, n)#均匀分布
y = np.random.uniform(y_min, y_max, n)
#统计落在函数y=x^2下方的点
res = sum(np.where(y < f(x), 1 ,0))
#计算定积分的近似值
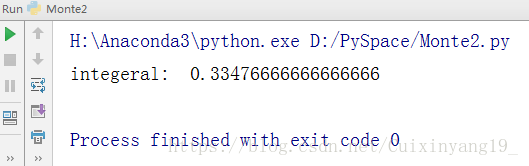
integral = res / n
print('integeral: ', integral)
# 画个图
fig = plt.figure()
axes = fig.add_subplot(111)
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') # 防止图像变形
axes.plot(np.linspace(x_min, x_max, 10), f(np.linspace(x_min, x_max, 10)), 'b-') # 函数图像
#plt.xlim(x_min, x_max)
plt.show()