4X4数字拼图的自动求解程序下载,手玩技巧及数学原理
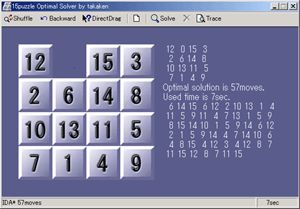
首先,推荐一款非常棒的4X4数字拼图的求解程序,是一个日本人写的,单个exe文件,快速求得最优解,并且可以动画演示。
"15puzzle Optimal solver" for windows
以下部分为转载:
* 益智游戏是一种较为大众化的应用数学,任何人不论对数学是否感兴趣,或多或少都会为它着迷。主要是因为它具有趣味性、消遣性及益智性,而不似一般数学那麽 的深奥及枯燥。当然最主要的是因为它的大众化,无需具有高深理论即可实施,故不分男女老幼及教育程度,都能享有这份乐趣!
* 数字拼图就是这样的一个数学益智游戏,每隔一段时间就会掀起一阵流行,在小朋友间尤其普及,是一个十分 迷人的个人操作游戏。
* 一般的游戏方式或市售的数字盘,是在一个 4 * 4 的盘面中放入 1~15 的数字,并保留一个空格,游戏者的任务是利用移动空格旁边的数字到空格中的方法,使得所有的数字由左而右、由上而下依序排列 (以下简称顺 序花式) ,所以本游戏也被叫做「移动十五」、「十五子棋」、「十五子迷」、「数字智慧盘」等。
* 其实这个游戏并不必限定在 4*4 的盘面中操作,但是市售的实体数字盘要做到任意改变大小似乎有点困难,而 且 4*4 的盘面难易度最为适中,所以大家就习以为常了。
* 数字拼图通常的玩法有下列几种:
* 数字拼图就是这样的一个数学益智游戏,每隔一段时间就会掀起一阵流行,在小朋友间尤其普及,是一个十分 迷人的个人操作游戏。
* 一般的游戏方式或市售的数字盘,是在一个 4 * 4 的盘面中放入 1~15 的数字,并保留一个空格,游戏者的任务是利用移动空格旁边的数字到空格中的方法,使得所有的数字由左而右、由上而下依序排列 (以下简称顺 序花式) ,所以本游戏也被叫做「移动十五」、「十五子棋」、「十五子迷」、「数字智慧盘」等。
* 其实这个游戏并不必限定在 4*4 的盘面中操作,但是市售的实体数字盘要做到任意改变大小似乎有点困难,而 且 4*4 的盘面难易度最为适中,所以大家就习以为常了。
* 数字拼图通常的玩法有下列几种:
- 第一种玩法:将数字盘中的数字方块全部倒出,然后随意的将数字方块装回盘中(以下简称随机花式),请游 戏者排出顺序花式。
8 4 7 9 12 13 10 3 5 15 1 11 6 14 2 ===> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ( 图 1 ) 随机花式一例。 - 第二种玩法:将数字盘中的数字方块先排成顺序花式,然后随意移动到满意为止(以下简称随移花式),请游戏者复原成顺序花式。
8 2 1 13 10 4 5 14 7 9 11 3 12 15 6 ===> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ( 图 2 ) 将数字方块随意移动后,再要求复原。 - 第三种玩法:游戏的目的花式不再是顺序花式,而是指定的任一种花式,请游戏者由目前花式转换过去。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 <===> 1 3 5 7 9 11 13 15 2 4 6 8 10 12 14 <===> 1 2 3 4 12 13 14 5 11 15 6 10 9 8 7 ( 图 3 ) 由指定的花式变成另一个花式。
研究问题
* 任何一个有经验的人都知道,既然第二种玩法旳随移花式是由顺序花式任意移动后造出的,那麽理论上, 只要顺着相反的顺序移动回去,当然可以还原成顺序花序,至于其他的两种玩法都会有无法达成目标的情形发生。
* 以图 1 左边的随机花式为例,如果你已掌握了操作的秘诀,应该可以很快的将它排成下图中央的逆序花式,在这种情况下,如果不把数字方块拿出盘面再放回去,而只用规定的移动方式,是绝对无法排出顺序花式的。
|
===> 可 |
|
===> 不可能 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| ( 图 4 ) 逆序花式和顺序花式。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
* 如果你的经验够丰富了,你会发现:所有的随机花式都可藉由规定的移动方式排成逆序花式和顺序花式之一, 无一例外。
* 当可以用规定的方式移动数字方块,使得某一随机花式排成顺序花式时,我们称之为有解,反之是为无解。
* 问题来了:
1. 如果已知某一个随机花式有解,该如何移动才能顺利达成目标呢?
2. 有没有一个简易的方法来判定怎样的随机花式有解,怎样的随机花式无解呢?
移动的操作技巧
* 稍有经验的人都知道,即使明知有解,但有些人就是可以在短时间内将数字东移西移,经过一番处理之后 迅速归位以完成任务,有些人却是千试万试,不论如何移动,就是无法把数字塞到指定的位置以完成任务。 其差别就在有没有理解并应用以下的一些移动技巧罢了。
* 要把数字 1、2 移入位置 1、2 ,因为几乎可说是没有任何限制,所以应该是不会有问题的,只是使用 的步数多少的差别而已。
* 本游戏的第一个考验来了,如果依样画葫芦,贸然把 数字 3 移入位置 3 后(如图 5),想把数字 4 移 入位置 4,如果不知道以退为进的道理,可能永远都在绕圈子。一般人初试数字拼图游戏,把数字 1、2、3 移入位置 1、2、3 后觉得容易,但在移入 4 时遇到大麻烦,如果没有人指点开窍, 很可能就心生畏怯,再也不踫本游戏了。以下把处理相关状况的技巧略举一二,只要学会其中的一个, 就可应付自如了。
* 状况一:1、2、3 已就位, 4 从左方来,如何让 4 就位?
本状况的处理,要打破已摆好位置的数字不要再动的迷思,否则虽也可用类似状况 3 、4 之解法,但求 解步骤将大幅增加。本解法也可适用于「5、6、7 已就位, 8 从左方来,如何让 6 就位?」的情形。
* 状况二:1、2、3 已就位, 4 从下方来,如何让 4 就位?
本状况也可适用于「5、6、7 已就位, 8 从下方来,如何让 8 就位?」的情形。
* 状况三:1、2、3 已就位, 4 从右下方来,如何让 4 就位?
本状况也可适用于「5、6、7 已就位, 8 从右下方来,如何让 8 就位?」的情形。
由解答示范的第一步竟然回头向下走,可以给我们一个警示,以后遇此状况,就不要向上去逼近是非之地比较好。
* 状况四:1、2 已就位, 如何让 3、4 就位?
本状况示范数字 3、4 都尚未就位时,比较节省移动步数的方法,尤怪把它叫做倒车入库,先把数字 3 放到位置 4 , 数字 4 移到数字 3 的下方后再倒退就位;有时则要以相反的方式处理:先把数字 4 放到位置 3 , 数字 3 移到数字 4 的下方后再倒退就位。如何应用要看盘面数字的相对位置而定,所谓应用之妙存乎一心是也。
* 状况五:上半部已就位, 如何让最后两列就位?
本示范提示我们:不管几行几列,上半部可以用状况 1~4 的着法一列一列摆好,但是最后两列一定要先把最左一 行的两个数字摆好位置,依次由左而右安排才好。对许多初学者来说,这也是一大障碍点。
* 掌握以上操作要领之后,保証能让你一路顺风,赶快披挂上阵,表现一下吧!
逆序和判别法
* 虽然已学会了移动的技巧,但稍有经验的人都知道,如果採用随机花式的玩法,将会有一半的机率出现无解的情形,花费了一番工夫之后才发现无解时,那种滋味可 真不好受。如果採用的是转换指定花式的玩法,尤其是有人出题互考时,最后才发现被以无解的情形来戏弄了,不也有点不甘心?所以如果学会了是否有解的判定法 之后,在移动前就判定了是否有解,不是反可让那些想戏弄我们的人被唬得一愣一愣的吗?
* 要判别指定的随机花式是否有解,逆序和判别法是较易于上手的方法。
* 本法判别的步骤如下:
1. 第一步:空格归位。
可以用任意的移动方式把空格移到右下角。以图 1 和图 2 的随机花式为例,图 11 和图 12 分别採用了不 同的归位方式。
|
===> |
|
||||||||||||||||||||||||||||||||
| ( 图 11 ) 以先下移后右移的方式将空格归位。 | ||||||||||||||||||||||||||||||||||
|
===> |
|
||||||||||||||||||||||||||||||||
| ( 图 12 ) 以先右移后下移的方式将空格归位。 | ||||||||||||||||||||||||||||||||||
2. 第二步:点数逆序的个数,并求其和。
把数字盘中的数字当成一个数列,其顺序为由左而右、由上而下,以图 11 右边的归位花式而言, 可看成是下面的数列
9, 8, 4, 7, 3, 12, 13, 10, 11, 5, 15, 1, 6, 14, 2
什麽是逆序呢? 当数列中较小的数字位置在较大数字的后方时,就是逆序。
以上面的数列为例,
数字 9 共有 8 个逆序,因为 1, 2, 3, 4, 5, 6, 7, 8 都在它的后方,
数字 8 共有 7 个逆序,因为 1, 2, 3, 4, 5, 6, 7 都在它的后方,
数字 4 共有 3 个逆序,因为 1, 2, 3 都在它的后方,
数字 7 共有 5 个逆序,因为 1, 2, 3, 5, 6 都在它的后方,
数字 3 共有 2 个逆序,因为 1, 2 都在它的后方,
数字 12 共有 6 个逆序,因为 1, 2, 5, 6, 10, 11 都在它的后方,
数字 13 共有 6 个逆序,因为 1, 2 5, 6, 10, 11 都在它的后方,
数字 10 共有 4 个逆序,因为 1, 2 5, 6 都在它的后方,
数字 11 共有 4 个逆序,因为 1, 2 5, 6 都在它的后方,
数字 5 共有 2 个逆序,因为 1, 2 都在它的后方,
数字 15 共有 4 个逆序,因为 1, 2, 6, 14 都在它的后方,
数字 1 共有 0 个逆序,因为它就是最小的数了,
数字 6 共有 1 个逆序,因为只有 2 在它的后方,
数字 14 也只有 1 个逆序,就是 2,
数字 2 已是数列中的最后一个数字了,当然没有逆序。
所以逆序和就是 8 + 7 + 3 + 5 + 2 + 6 + 6 + 4 + 4 + 2 + 4 + 0 + 1 + 1 = 53
3. 第三步:判定。逆序和为偶是有解,为奇则无解。
由于图 5 的逆序和为 53,所以图 11 的随机花式无解。
请读者自行计算试试,图 12 的归位花式其逆序和为 38,所以图 12 的随机花式有解。
想到了吗?在第二步计算逆序和时,其实可以偷一下懒,只注意和是奇偶就好, 不必老老实实的加总,那很累的!(看不懂?没关係!当做尤怪我没说就好了)
* 因为我们的目的花式(顺序花式)逆序和为 0 是偶数,所以所有有解的花式也一定是偶数逆序和。
如果我们的目的花式(例如逆序花式)逆序和是奇数,则所有有解的花式也一定是奇数的逆序和。
轮换判别法
* 要判别指定的随机花式是否有解,逆序和判别法虽然较易于上手,但是点数起来有点麻烦不是吗? 如果你有同感,那试试轮换判别法吧!
* 本法判别的步骤如下:
1. 第一步:空格归位。同逆序和判别法之操作。
2. 第二步:写出轮换的连乘积。
同样的把数字盘中的数字看成是一个由左而右、由上而下的数列,以图 11 右边的归位花式而言, 可看成是下面的数列
9, 8, 4, 7, 3, 12, 13, 10, 11, 5, 15, 1, 6, 14, 2
由数字 1 开始检验,如果它的位置和数值不符,就要开始以下製作轮换的过程:
这个轮换的第一个数字是数值 1,它的位置跑到位置 12 去了,记成 (1, 12
位置 12 应该是数值 12,但它却跑到位置 6 去了,记成 (1, 12, 6
位置 6 应该是数值 6,但它却跑到位置 13 去了,记成 (1, 12, 6, 13
位置 13 应该是数值 13,但它却跑到位置 7 去了,记成 (1, 12, 6, 13, 7
位置 7 应该是数值 7,但它却跑到位置 4 去了,记成 (1, 12, 6, 13, 7, 4
位置 4 应该是数值 4,但它却跑到位置 3 去了,记成 (1, 12, 6, 13, 7, 4, 3
位置 3 应该是数值 3,但它却跑到位置 5 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5
位置 5 应该是数值 5,但它却跑到位置 10 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10
位置 10 应该是数值 10,但它却跑到位置 8 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8
位置 8 应该是数值 8,但它却跑到位置 2 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2
位置 2 应该是数值 2,但它却跑到位置 15 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15
位置 15 应该是数值 15,但它却跑到位置 11 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15, 11
位置 11 应该是数值 11,但它却跑到位置 9 去了,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15, 11, 9
位置 9 应该是数值 9,但它却跑到位置 1 去了,但因为这个轮换的起始数就是 1,所以轮换结束,记成 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15, 11, 9)
不包括在这个轮换的数值只剩下 14,而它恰好也在位置 14,所以不必製作另一个轮换。图 11 的归位花式轮换积就是 (1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15, 11, 9) 了。
3. 第三步:判定轮换积是偶排列或奇排列。
把每一个轮换的元素个素减 1后相加,其和就姑且称之为长度吧!长度为偶数的轮换积叫做偶排列,长度 为奇数的轮换积就叫做奇排列。
(1, 12, 6, 13, 7, 4, 3, 5, 10, 8, 2, 15, 11, 9) 只有一个轮换且元素个数为 14,所以长度为 13, 是奇排列。
4. 第四步:判定。若为偶排列则有解,为奇排列则无解。
由于图 11 对应的轮换积是奇排列,所以图 11 的随机花式无解。
请读者自行试试,图 12 对应的轮换积为 (1, 3, 13, 4, 6, 12, 14, 8)(5, 7, 9, 10), 所以长度为 ( 8 - 1)+ ( 4 - 1 ) = 10 是偶排列,所以有解。
* 因为我们的目的花式(顺序花式)是偶排列,所以所有有解的花式也一定是偶排列。
如果我们的目的花式(例如逆序花式)是奇排列,则所有有解的花式也一定是奇排列。
结语
* 以上的示范及讨论都是用一般的 4 * 4 盘面,如果改换成 n * m 的盘面时,是否也可以依样画葫芦呢? 是的,以上的方法及结论全部适用。
* 那麽市售的实体数字盘或一般的玩法为什麽大都是採用4*4 的盘面呢?除了实体数字盘要做到任意改变大小 实在非常困难外,另一个原因就是 3 * 3 的盘面只有数字 1 的归位是简单的,其他的每一个数字要归位都 要大费思量,而 5 * 5 以上的盘面,有一半以上的数字都毫无挑战性,最右两行及最下两列虽然是比较有困难度的,但是能解决两个,就表示已掌握了移动的技巧了,再多的类似情况也可 顺利过关,所以并无意义。 4*4 的盘面难易度因此最为适中,所以大家就习以为常了。
转自:http://home.educities.edu.tw/oddest/math1621.htm (链接已失效)
转自:http://hi.baidu.com/uehe/blog/item/35f67116c642914e20a4e917.html