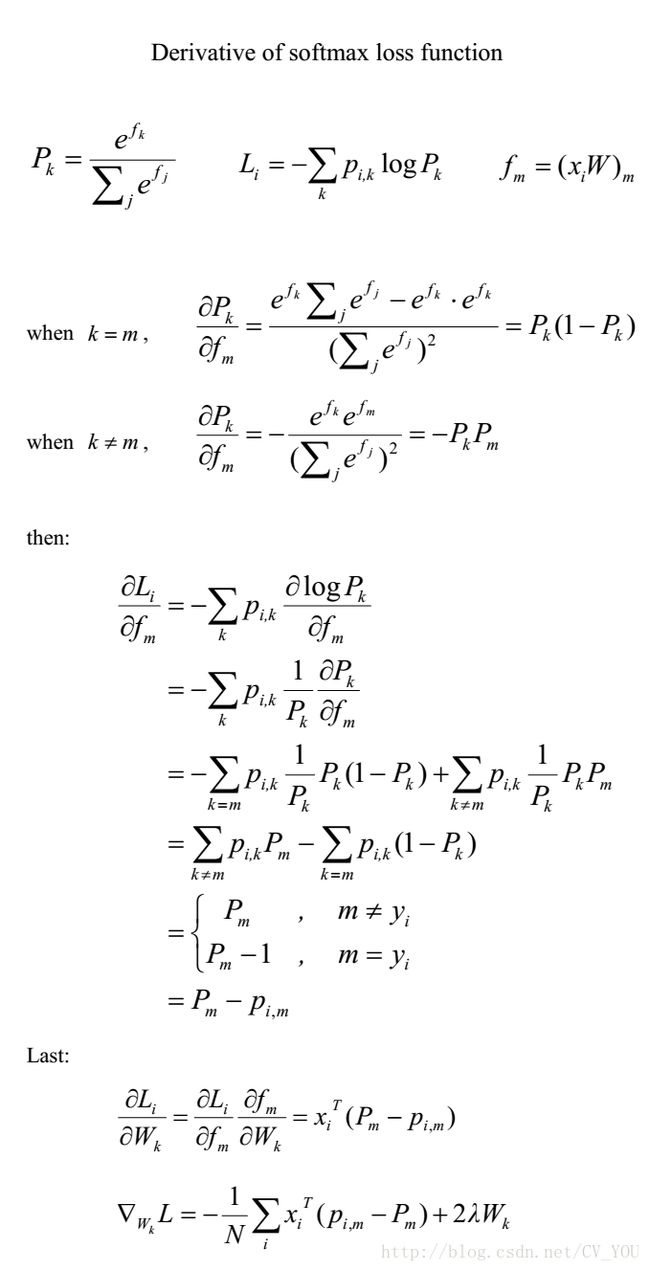机器学习(5)-理解softmax的损失函数和梯度表达式的实现+编程总结
softmax也是一个用于多分类的线性分类器。
首先来看看softmax的损失函数和梯度函数公式
结合惩罚项,给出总的损失函数:
L = -(1/N)∑i∑j1(k=yi)log(exp(fk)/∑j exp(fj)) + λR(W)
下面有几个准备函数也要理解:
Li = -log(exp(fyi)/∑j exp(fj)) :这个就是最基本的softmax函数,也就是本应该正确的分类得分在所有的类得分的比例,也可以说概率。
在实际编程计算softmax函数时,可能会遇到数值稳定性(Numeric stability)问题(因为在计算过程中,exp(fyi) 和 ∑j exp(fj) 的值可能会变得非常大,大值数相除容易导致数值不稳定),为了避免出现这样的问题,我们可以进行如下处理

其中,C的取值通常为:logC = -maxj fj,即-logC取f每一行中的最大值。
现在,结合惩罚项,给出总的损失函数:
L = -(1/N)∑i∑j1(k=yi)log(exp(fk)/∑j exp(fj)) + λR(W)
理解:其实就是图片矩阵得X,每一行中本该得分正确的得分的值除以那一行所有的类的得分和,得到一个概率,在把每一行得到的概率加起来,置于公式里面的exp,log加上取就好,logC的引入也就解释,就是为了数值稳定性。
这里面的pi,m,当样本分类正确时候,取1,其他元素取0,pm为p[i,m],表示第i张图片在第m个分类上的概率。确实这里(pi,m-Pm)要明白怎么代码实现。
下面看看For循环代码
def softmax_loss_naive(W, X, y, reg):
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_train = X.shape[0]
num_class = W.shape[1]
print (num_train,':',num_class)
scores = X.dot(W)
scores_max = np.reshape(np.max(scores,axis =1),(num_train,1))
prob = np.exp(scores - scores_max)/np.sum(np.exp( scores - scores_max ),axis =1,keepdims =True)#这里的keepdims必须加上,否则不同维度的矩阵不能进行操作。
#N*C
correct_prob = np.zeros_like(prob)
correct_prob[np.arange(num_train),y] =1
for i in range(num_train):
for j in range(num_class):
loss += -( correct_prob[i,j]* np.log(prob[i,j]) )
dW[:,j] += (prob[i,j] - correct_prob[i,j])*X[i,:]
# if j==y[i]:
# loss += (-np.log(prob[i,j]))
# dW[:,j] -=(1-prob[i,j])*X[i,:]
# else:
# dW[:,j] -= (0-prob[i,j]) * X[i]
#上面求梯度的两行代码,j就相当于公式中的m,遍历所有的分类,得到一张图对应的一个[N*C]权重矩阵dW,然后讲每个i对应的dW相加。
loss = loss/num_train
loss = loss + 0.5*reg*np.sum(W*W)
dW = dW/num_train
dW += reg*W
return loss, dW
下面看看矩阵操作实现:
def softmax_loss_vectorized(W, X, y, reg):
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using no explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_train = X.shape[0]
scores = X.dot(W)
scores_max= np.max(scores,axis =1)
scores_max = np.reshape(scores_max,(num_train,1))
scores_correct = scores[np.arange(num_train), y]
scores_1 = scores -scores_max
scores_correct_1 =scores_correct -scores_max
prob = np.exp(scores_1) /np.sum(np.exp(scores_1),axis =1,keepdims= True)#caculatie the problity of each score N*C
keep_prob = np.zeros_like(prob)
keep_prob[np.arange(num_train),y] =1
#prob =np.log(np.exp(scores_correct_1)) / np.sum((np.log(np.exp(scores_1)
# loss = np.sum( np.log(np.exp(scores_correct_1)) / np.sum((np.log(np.exp(scores_1))),1) )
loss += np.sum(keep_prob*np.log(prob ))
loss =loss/num_train*(-1)
loss =loss + 0.5*reg*np.sum(W*W)
# print ('loss1:',loss)
dW += X.T.dot(keep_prob - prob) #这一句话就是最重要的一句话。也是softmax矩阵操作核心
dW = -dW/num_train+reg*W
# dW += -np.dot(X.T,keep_prob -prob)/num_train +reg*W
return loss, dW
有了loss和gradient,通过梯度下降法来优化权重矩阵W了。
self.W += -learning_rate*grad也就是这句话。
好了,这两个算法吧还要慢慢在实际使用中慢慢加深了理解。