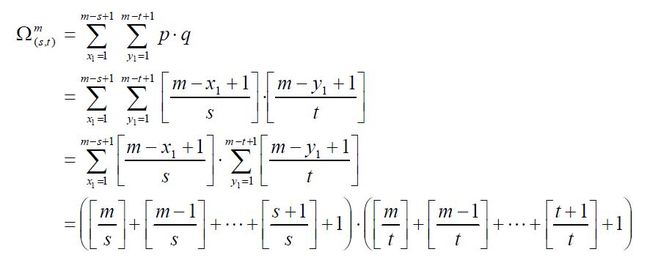opencv:特征检测与提取——Hog、LBP、Haar-like
废话不多说了,直接切入正题,本文将介绍另外三种特征提取算法:HOG,LBP,Haar。首先,让我们了解一下HOG算法
一:HOG特征提取
概述
在一副图像中,局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。(本质:梯度的统计信息,而梯度主要存在于边缘的地方)。HOG特征提取的目标其实就是这些局部区域的表象和形状,该算法大致的实现过程是:首先将图像分成小的连通区域,我们把它叫细胞单元,如果不理解什么是细胞单元也没关系,后面会详细说。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。
方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。Hog特征结合SVM分类器已经被广泛应用于图像识别中,尤其在行人检测中获得了极大的成功。需要提醒的是,HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的,而如今虽然有很多行人检测算法不断提出,但基本都是以HOG+SVM的思路为主。
接下来,我们将具体说说HOG特征提取的每一个步骤。
预处理:gamma矫正
为了减少光照因素的影响,首先需要将整个图像进行规范化(归一化)。在图像的纹理强度中,局部的表层曝光贡献的比重较大,所以,这种压缩处理能够有效地降低图像局部的阴影和光照变化。因为颜色信息作用不大,通常先转化为灰度图; Gamma压缩公式为:
![]()
比如可以取Gamma=1/2;对gamma矫正不熟悉的朋友,可以参考这里。
计算图像的梯度
计算图像横坐标和纵坐标方向的梯度,并据此计算每个像素位置的梯度方向值;求导操作不仅能够捕获轮廓,人影和一些纹理信息,还能进一步弱化光照的影响。
图像中像素点(x,y)的梯度为:
![]()
![]()
上式中,![]() 分别表示输入图像中像素点(x,y)处水平方向梯度,竖直方向梯度以及像素值。该像素点的梯度幅值和梯度方向分别为:
分别表示输入图像中像素点(x,y)处水平方向梯度,竖直方向梯度以及像素值。该像素点的梯度幅值和梯度方向分别为:
最常用的方法就是利用Sobel算子计算梯度,不理解Sobel算子计算梯度的朋友可以点击这里,然后再用以上公式计算该像素点的梯度大小和方向,下图为运用Sobel算子处理的图像效果。
为每个细胞单元构建梯度方向直方图
这一步的目的就是给局部图像区域构造特征向量,该特征向量中保持了图像中人体对象的姿势和外观的弱敏感性。
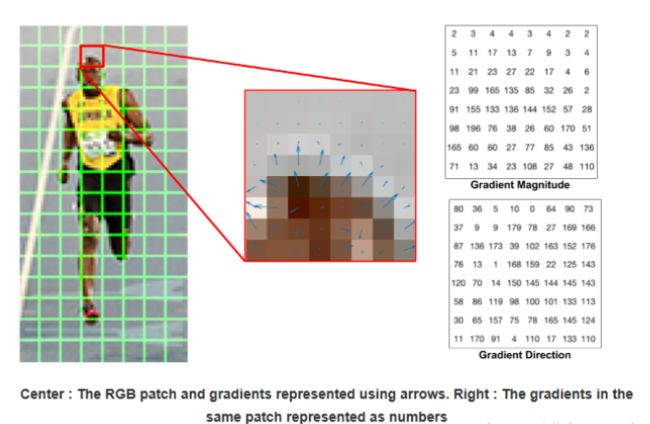
我们将图像分成若干个“单元格cell”,例如每个cell为8*8个像素,(为什么用8*8像素为一个cell?这是我们通过特征缩放来寻找到的明确的选择。HOG最初用于检测行人。在一张行人照片缩放到64×128,使用8×8像素构造细胞单元足以捕捉有趣的功能)。下图为一个细胞单元内像素的梯度信息,包含梯度值和梯度方向。
在图的右边,我们看到原始的数字表示在8×8像素细胞单元有一个小的差异,那就是角度是0度和180度的梯度,而不是0到360度之间。这些被称为“无符号”渐变,因为梯度正值和它的负值用相同的数字表示。换句话说,梯度箭头和与之相对的180度箭头被认为是相同的。为什么不使用0 - 360度呢?经验表明,无符号梯度比符号梯度更好地用于行人检测。HOG的一些实现将允许您指定是否使用带符号的渐变。
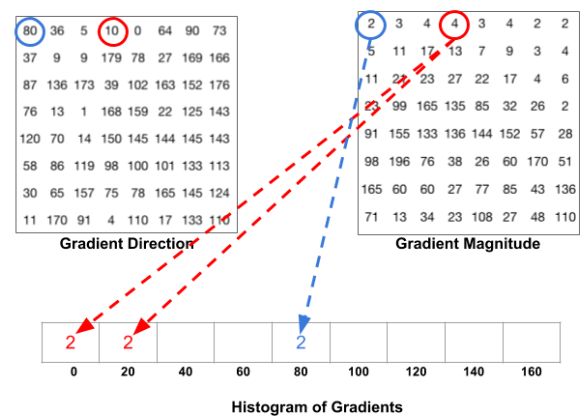
然后我们采用9个bin的直方图来统计这8*8个像素的梯度信息,直方图的9个bin对应角度0, 20, 40…160。
下图说明了这个过程。我们在前面的图寻找到了8×8像素细胞单元中每一个像素梯度的幅值和方向。根据方向选择箱子,并根据大小选择进入箱子的值。让我们首先关注环绕在蓝色中的像素。它的角度(方向)为80度,大小为2。所以它放入到第五个箱子。用红色包围的像素的梯度方向为10度,大小为4。由于10度是0和20之间的一半,所以像素的也是均匀地分成两个箱子。
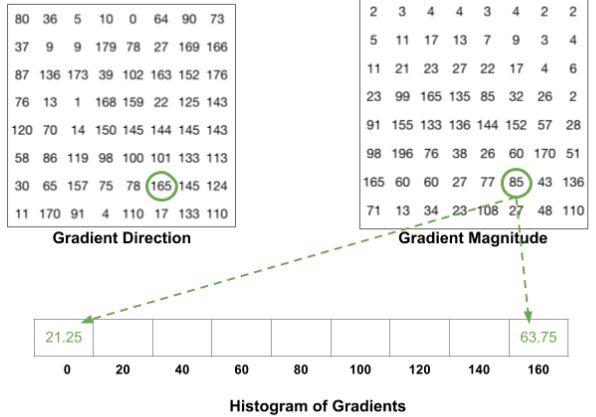
还有一个细节需要注意。如果角度大于160度,则在160到180之间,我们知道角度绕成0和180相等。因此,在下面的例子中,角度为165度的像素正比于0度的箱子和160度的箱子。
因为180-165/165-160=3 ,所以0箱子分4/1,160箱子分4/3。如下所示:
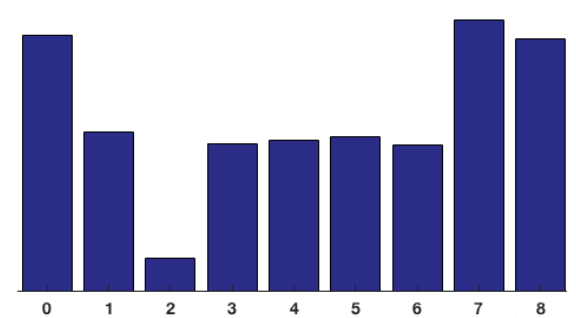
在8×8像素的细胞单元中所有像素的贡献加起来构造9-bin直方图,它看起来像这样:
在我们的表示中,y轴是0度。你可以看到直方图在0度和180度附近占很大比重。
16x16像素block归一化
由于局部光照的变化以及前景-背景对比度的变化,使得梯度强度的变化范围非常大。这就需要对梯度强度做归一化。归一化能够进一步地对光照、阴影和边缘进行压缩。我们把各个细胞单元组合成大的、空间上连通的区间(blocks)。这样,一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的,这就意味着:每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。我们将归一化之后的块描述符(向量)就称之为HOG描述符。
例如在行人检测中,图像大小为64*128,我们的细胞单元大小为8*8像素大小,那么我们将每2*2个cell组成一个block,也就是一个block内有16*16像素,因此之前一个cell里面有9个特征,因此一个block将4个cell的特征串联,就有4*9=36个特征,然后,我们将这36个特征进行最大最小值归一化。
我们以8个像素为步长滑动这个block,水平方向我们可以扫描出7个block,竖直方向可以扫描出15个block,因此64*128的图像最后的特征有36*7*15=3780个特征。下图显示了定向梯度直方图的可视化:
HOG算法实践:
HOGDescriptor(Size win_size=Size(64, 128),
Size block_size=Size(16, 16),
Size block_stride=Size(8, 8),
Size cell_size=Size(8, 8),
int nbins=9,
double win_sigma=DEFAULT_WIN_SIGMA,
double threshold_L2hys=0.2,
bool gamma_correction=true,
int nlevels=DEFAULT_NLEVELS
) 参数注释:
<1>win_size:检测窗口大小。
<2>block_size:块大小,目前只支持Size(16, 16)。
<3>block_stride:块的滑动步长,大小只支持是单元格cell_size大小的倍数。
<4>cell_size:单元格的大小,目前只支持Size(8, 8)。
<5>nbins:直方图bin的数量(投票箱的个数),目前每个单元格Cell只支持9个。
<6>win_sigma:高斯滤波窗口的参数。
<7>threshold_L2hys:块内直方图归一化类型L2-Hys的归一化收缩率
<8>gamma_correction:是否gamma校正
<9>nlevels:检测窗口的最大数量
HOG行人检测
#include
#include
using namespace cv;
using namespace std;
int main(void)
{
Mat input = imread("D:/opencv/testPeople.png");
if (input.empty())
return 1;
Mat src = input.clone();
//这一部分是如何计算HOG特征描述子
/*
Mat dst, dst_gray;
resize(src, dst, Size(64, 128)); //调整大小
cvtColor(dst, dst_gray, CV_BGR2GRAY); //转换成灰度图像
HOGDescriptor detector(Size(64, 128), Size(16, 16), Size(8, 8), Size(8, 8), 9); //创造一个HOG检测器
vector descriptor; //HOG描述子
vector location; //局部区域的位置
detector.compute(dst_gray, descriptor, Size(0, 0), Size(0, 0), location);
cout << "descriptor size " << descriptor.size(); //观察是否是3780个特征
*/
//下面是调用opencv中集成的基于HOG的SVM行人检测数据集,进行行人检测
HOGDescriptor hog = HOGDescriptor(); //创造一个HOG检测器
hog.setSVMDetector(hog.getDefaultPeopleDetector()); //设置线性SVM分类器
vector peopleLocation; //检测处的行人边缘位置
//多尺度检测,1.05是窗口增长参数,Size(8, 8)为窗口步长,必须是块步长的整数倍,Size(16, 16)为模拟参数
//2.0表示调节相似性系数的阈值。检测到时,某些对象可以由许多矩形覆盖。 0表示不进行分组。
hog.detectMultiScale(src, peopleLocation, 0, Size(8, 8), Size(16, 16), 1.05, 2.0);
for (int i = 0; i < peopleLocation.size(); ++i)
{
rectangle(src, peopleLocation[i], Scalar(0, 0, 255)); //画出检测边缘
}
imshow("input", input);
imshow("src", src);
cvWaitKey();
return 0;
} 我随便在网上弄得一个图,效果如下:
二:LBP特征提取
LBP指局部二值模式,英文全称:Local Binary Pattern,是一种用来描述图像局部特征的算子,LBP特征具有灰度不变性和旋转不变性等显著优点。由于LBP特征计算简单、效果较好,因此LBP特征在计算机视觉的许多领域都得到了广泛的应用,LBP特征比较出名的应用是用在人脸识别和目标检测中,在计算机视觉开源库OpenCV中有使用LBP特征进行人脸识别的接口,也有用LBP特征训练目标检测分类器的方法,Opencv实现了LBP特征的计算,但没有提供一个单独的计算LBP特征的接口。
LBP特征的原理
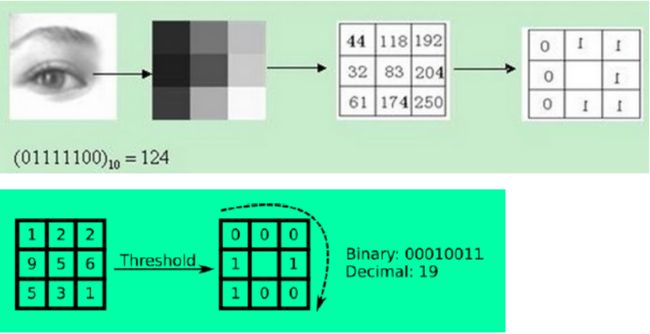
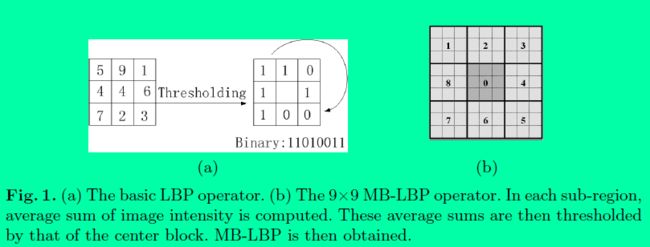
原始的LBP算子定义在像素3*3的邻域内,以邻域中心像素为阈值,相邻的8个像素的灰度值与邻域中心的像素值进行比较,若周围像素大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3邻域内的8个点经过比较可产生8位二进制数,将这8位二进制数依次排列形成一个二进制数字,这个二进制数字就是中心像素的LBP值,LBP值共有2的8次方种可能,因此LBP值有256种。中心像素的LBP值反映了该像素周围区域的纹理信息。
备注:计算LBP特征的图像必须是灰度图,如果是彩色图,需要先转换成灰度图。
上述过程用图像表示为:
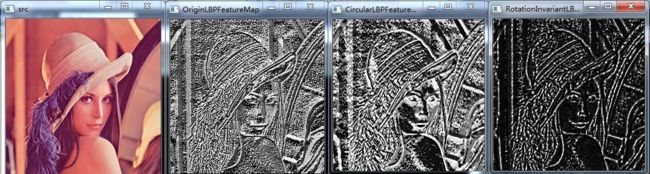
测试结果如下所示:
LBP的改进
在原始的LBP特征提出以后,研究人员对LBP特征进行了很多的改进,因此产生了许多LBP的改进版本。
由于原始LBP特征使用的是固定邻域内的灰度值,因此当图像的尺度发生变化时,LBP特征的编码将会发生错误,LBP特征将不能正确的反映像素点周围的纹理信息,因此研究人员对其进行了改进。基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,可以将 3×3 邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子:
这种LBP特征叫做Extended LBP,也叫Circular LBP。使用可变半径的圆对近邻像素进行编码,可以得到如下的近邻:
通过LBP特征的定义可以看出,LBP特征对光照变化是鲁棒的,也就是LBP的灰度不变性,那么怎么理解这个灰度不变性呢,所谓的灰度不变性,指的是光照变化是否会对描述产生影响,以上面的8邻域为例,光照变化是很难改变中心灰度值与其周围8个像素的大小关系的。因为光照是一种区域性质的变化,而不是单像素性质的变化。所以比如有一个强光照在这9个像素上面,这9个值应该是都会增大。
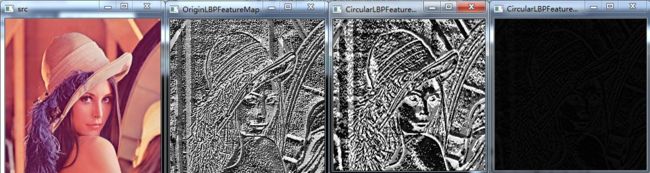
其效果如下图所示:
接下来我们测试一下改变邻域的半径大小以及邻域内采样像素点的数目个数后,LBP特征的变化:
上图第三幅图像为radius = 3,neighbors = 8,第四幅图像为radius = 1,neighbors = 8,从实验结果可以看出,半径越小,图像纹理越精细 。
上图第三幅图像为radius = 3,neighbors = 8,第四幅图像为radius = 3,neighbors = 4,从实验结果可以看出,邻域数目越小,图像亮度越低。
旋转不变LBP特征
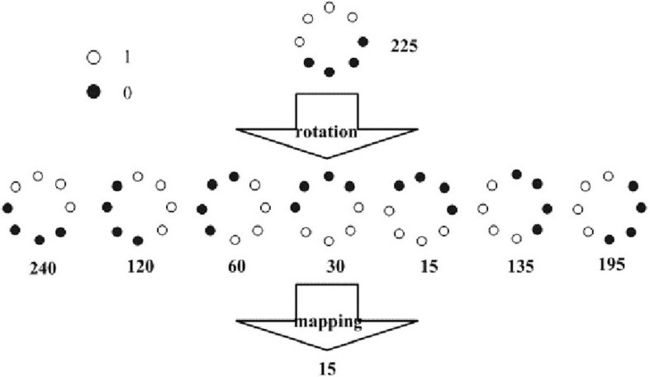
从上面可以看出,上面的LBP特征具有灰度不变性,但还不具备旋转不变性,因此研究人员又在上面的基础上进行了扩展,提出了具有旋转不变性的LBP特征。
如图,通过对得到的LBP特征进行旋转,得到一系列的LBP特征值,最终将特征值最小的一个特征模式作为中心像素点的LBP特征。
测试:
上图radius = 3,neighbors = 8,最后一幅是旋转不变LBP特征。
Uniform Pattern LBP特征
Uniform Pattern,也被称为等价模式或均匀模式,由于一个LBP特征有多种不同的二进制形式,对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生2^P种模式。很显然,随着邻域集内采样点数的增加,二进制模式的种类是以指数形式增加的。例如:5×5邻域内20个采样点,有2^20=1,048,576种二进制模式。这么多的二进制模式不利于纹理的提取、分类、识别及存取。例如,将LBP算子用于纹理分类或人脸识别时,常采用LBP模式的统计直方图来表达图像的信息,而较多的模式种类将使得数据量过大,且直方图过于稀疏。因此,需要对原始的LBP模式进行降维,使得数据量减少的情况下能最好的表示图像的信息。
为了解决二进制模式过多的问题,提高统计性,Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)。通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的2^P种减少为 P ( P-1)+2种(等价模式个数的推导可以参看这里),其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,即:它把值分为59类,58个uniform pattern为一类,其它的所有值为第59类。这样直方图从原来的256维变成59维。这使得特征向量的维数更少,并且可以减少高频噪声带来的影响.
具体实现:采样点数目为8个,即LBP特征值有2^8种,共256个值,正好对应灰度图像的0-255,因此原始的LBP特征图像是一幅正常的灰度图像,而等价模式LBP特征,根据0-1跳变次数,将这256个LBP特征值分为了59类,从跳变次数上划分:跳变0次—2个,跳变1次—0个,跳变2次—56个,跳变3次—0个,跳变4次—140个,跳变5次—0个,跳变6次—56个,跳变7次—0个,跳变8次—2个。共9种跳变情况,将这256个值进行分配,跳变小于2次的为等价模式类,共58个,他们对应的值按照从小到大分别编码为1—58,即它们在LBP特征图像中的灰度值为1—58,而除了等价模式类之外的混合模式类被编码为0,即它们在LBP特征中的灰度值为0,因此等价模式LBP特征图像整体偏暗。
MB-LBP特征
MB-LBP特征,全称为Multiscale Block LBP,MB-LBP的原理:
将图像分成一个个小块(Block),每个小块再分为一个个的小区域(类似于HOG中的cell),小区域内的灰度平均值作为当前小区域的灰度值,与周围小区域灰度进行比较形成LBP特征,生成的特征称为MB-LBP,Block大小为3*3,则小区域的大小为1,就是原始的LBP特征,上图的Block大小为9*9,小区域的大小为3*3。
不同Block提取的MB-LBP特征如图所示:
对得到LBP特征进行均值模式编码,通过对得到的特征图求直方图,得到了LBP特征值0-255之间(0-255即直方图中的bin)的特征数量,通过对bin中的数值进行排序,通过权衡,将排序在前63位的特征值看作是等价模式类,其他的为混合模式类,总共64类,称之为SEMB-LBP(Statistically Effective MB-LBP )。类似于等价模式LBP,等价模式的LBP的等价模式类为58种,混合模式类1种,共59种。二者除了等价模式类的数量不同之外,主要区别在于:对等价模式类的定义不同,等价模式LBP是根据0-1的跳变次数定义的,而SEMB-LBP是通过对直方图排序得到的。当然下一步要做的就是将SEMB-LBP变为LBPH进行使用。
MB-LBP有点类似于先将图像进行平滑处理,然后再求LBP特征。而SEMB-LBP是在MB-LBP进行编码后的图像。类似于等价模式LBP,先求LBP特征,再用等价模式进行编码。当Scale=3时,MB-LBP和SEMB-LBP就是LBP和等价模式LBP。想具体了解需要去看论文,当然要自己实现才会理解的更透彻。
LBPH——图像的LBP特征向量
LBPH,Local Binary Patterns Histograms,即LBP特征的统计直方图,LBPH将LBP特征与图像的空间信息结合在一起。将LBP特征图像分成m个局部块,并提取每个局部块的直方图,然后将这些直方图依次连接在一起形成LBP特征的统计直方图,即LBPH,有点类似HOG里面的梯度直方图吧。
- 将LBP特征图像进行分块,Opencv中默认将LBP特征图像分成8行8列64块区域
- 计算每块区域特征图像的直方图cell_LBPH,将直方图进行归一化,直方图大小为1*numPatterns,将上面计算的每块区域特征图像的直方图按分块的空间顺序依次排列成一行,形成LBP特征向量,大小为64*(1*numPatterns),用机器学习的方法对LBP特征向量进行训练,用来检测和识别目标
举例说明LBPH的维度: 采样点为8个,如果用的是原始的LBP或Extended LBP特征,其LBP特征值的模式为256种,则一幅图像的LBP特征向量维度为:64*256=16384维, 而如果使用的是等价模式LBP特征,其LBP值的模式为59种,其特征向量维度为:64*59=3776维,可以看出,使用等价模式特征,其特征向量的维度大大减少, 这意味着使用机器学习方法进行学习的时间将大大减少,而性能上没有受到很大影响。
LBP代码实现
原始的LBP特征计算:
#include
#include
using namespace std;
using namespace cv;
const char* output_iamge = "oriLBP Result";
int main() {
Mat src = imread("D:/opencv/yuner.jpg");
Mat gray_src;
namedWindow("imput image", CV_WINDOW_AUTOSIZE);
namedWindow(output_iamge, CV_WINDOW_AUTOSIZE);
imshow("imput image", src);
//灰度转换
cvtColor(src, gray_src, COLOR_BGR2GRAY);
int width = gray_src.cols;
int height = gray_src.rows;
Mat lbpImage = Mat::zeros(height - 2, width - 2, CV_8UC1);
for (int row = 1; row < height - 1; row++) {
for (int col = 1; col < width - 1; col++) {
uchar centerPix = gray_src.at(row, col);
uchar lbpCode = 0;
//编码中心点像素周围的像素
lbpCode |= (gray_src.at(row - 1, col - 1) > centerPix) << 7;
lbpCode |= (gray_src.at(row - 1, col) > centerPix) << 6;
lbpCode |= (gray_src.at(row - 1, col + 1) > centerPix) << 5;
lbpCode |= (gray_src.at(row , col + 1) > centerPix) << 4;
lbpCode |= (gray_src.at(row + 1, col + 1) > centerPix) << 3;
lbpCode |= (gray_src.at(row + 1, col) > centerPix) << 2;
lbpCode |= (gray_src.at(row + 1, col - 1) > centerPix) << 1;
lbpCode |= (gray_src.at(row , col - 1) > centerPix) << 0;
lbpImage.at(row - 1, col - 1) = lbpCode;
}
}
imshow(output_iamge, lbpImage);
waitKey(0);
return 0;
} 测试效果:
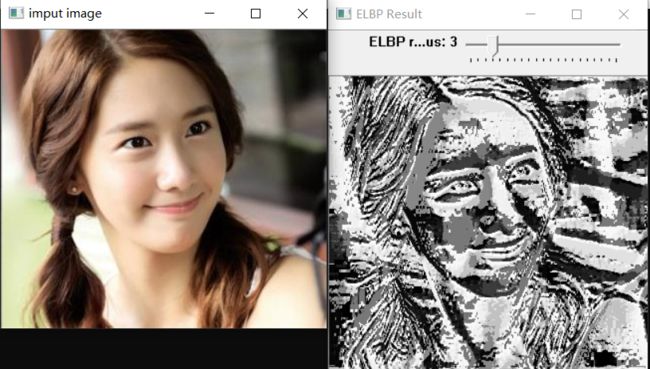
LBP扩展与多尺度表达(ELBP)
#include
#include
using namespace std;
using namespace cv;
const char* output_iamge1 = "ELBP Result";
int cur_radius = 3;
int max_count = 20;
Mat gray_src;
void ELBP_demo(int, void*);
int main() {
Mat src = imread("D:/opencv/yuner.jpg");
cvtColor(src, gray_src, COLOR_BGR2GRAY);
namedWindow("imput image", CV_WINDOW_AUTOSIZE);
namedWindow(output_iamge1, CV_WINDOW_AUTOSIZE);
imshow("imput image", src);
createTrackbar("ELBP radius", output_iamge1, &cur_radius, max_count, ELBP_demo);
ELBP_demo(0, 0);
waitKey(0);
return 0;
}
void ELBP_demo(int,void*) {
int width = gray_src.cols;
int height = gray_src.rows;
Mat ELBPImage = Mat::zeros(height - 2 * cur_radius, width - 2 * cur_radius, CV_8UC1);
int numNeighbors = 8;
for (int n = 0; n < numNeighbors; n++) {
//计算采样点对于中心点坐标的偏移量rx,ry,计算方式结合圆形编码理解
float rx = static_cast((cur_radius) * cos(2 * CV_PI * n / static_cast(numNeighbors)));
float ry = -static_cast((cur_radius) * sin(2 * CV_PI * n / static_cast(numNeighbors)));
//为双线性插值做准备
//对采样点偏移量分别进行上下取整
int x1 = static_cast(floor(rx));
int x2 = static_cast(ceil(rx));
int y1 = static_cast(floor(ry));
int y2 = static_cast(ceil(ry));
//将坐标偏移量映射到0-1之间
float tx = rx - x1;
float ty = ry - y1;
//根据0-1之间的x,y的权重计算公式计算权重,权重与坐标具体位置无关,与坐标间的差值有关
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
for (int i = cur_radius; i < height - cur_radius; i++)
{
for (int j = cur_radius; j < width - cur_radius; j++)
{
//获得中心像素点的灰度值
uchar centerPix = gray_src.at(i, j);
//根据双线性插值公式计算第k个采样点的灰度值
float neighbor = gray_src.at(i + x1, j + y1) * w1 + gray_src.at(i + x1, j + y2) *w2 \
+ gray_src.at(i + x2, j + y1) * w3 + gray_src.at(i + x2, j + y2) *w4;
//LBP特征图像的每个邻居的LBP值累加,累加通过或操作完成,对应的LBP值通过移位取得
ELBPImage.at(i - cur_radius, j - cur_radius) |= (neighbor > centerPix) << (numNeighbors - n - 1);
}
}
}
imshow(output_iamge1, ELBPImage);
} 测试效果:
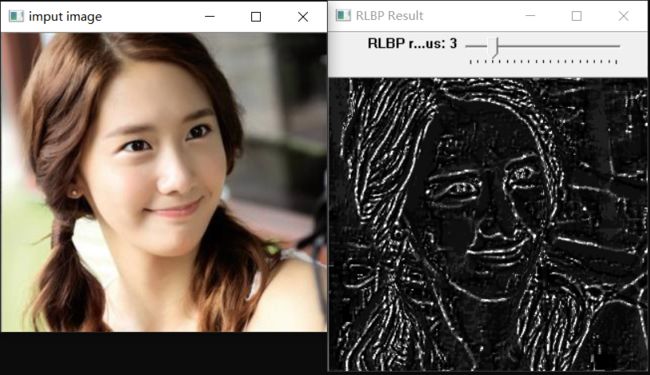
旋转不变LBP
#include
#include
using namespace std;
using namespace cv;
const char* output_iamge1 = "RLBP Result";
int cur_radius = 3;
int max_count = 20;
Mat gray_src;
void ELBP_demo(int, void*);
int main() {
Mat src = imread("D:/opencv/yuner.jpg");
cvtColor(src, gray_src, COLOR_BGR2GRAY);
namedWindow("imput image", CV_WINDOW_AUTOSIZE);
namedWindow(output_iamge1, CV_WINDOW_AUTOSIZE);
imshow("imput image", src);
createTrackbar("RLBP radius", output_iamge1, &cur_radius, max_count, ELBP_demo);
ELBP_demo(0, 0);
waitKey(0);
return 0;
}
void ELBP_demo(int,void*) {
int width = gray_src.cols;
int height = gray_src.rows;
Mat RLBPImage = Mat::zeros(height - 2 * cur_radius, width - 2 * cur_radius, CV_8UC1);
int numNeighbors = 8;
for (int n = 0; n < numNeighbors; n++) {
//计算采样点对于中心点坐标的偏移量rx,ry,计算方式结合圆形编码理解
float rx = static_cast((cur_radius) * cos(2 * CV_PI * n / static_cast(numNeighbors)));
float ry = -static_cast((cur_radius) * sin(2 * CV_PI * n / static_cast(numNeighbors)));
//为双线性插值做准备
//对采样点偏移量分别进行上下取整
int x1 = static_cast(floor(rx));
int x2 = static_cast(ceil(rx));
int y1 = static_cast(floor(ry));
int y2 = static_cast(ceil(ry));
//将坐标偏移量映射到0-1之间
float tx = rx - x1;
float ty = ry - y1;
//根据0-1之间的x,y的权重计算公式计算权重,权重与坐标具体位置无关,与坐标间的差值有关
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
for (int i = cur_radius; i < height - cur_radius; i++)
{
for (int j = cur_radius; j < width - cur_radius; j++)
{
//获得中心像素点的灰度值
uchar centerPix = gray_src.at(i, j);
//根据双线性插值公式计算第k个采样点的灰度值
float neighbor = gray_src.at(i + x1, j + y1) * w1 + gray_src.at(i + x1, j + y2) *w2 \
+ gray_src.at(i + x2, j + y1) * w3 + gray_src.at(i + x2, j + y2) *w4;
//LBP特征图像的每个邻居的LBP值累加,累加通过或操作完成,对应的LBP值通过移位取得
RLBPImage.at(i - cur_radius, j - cur_radius) |= (neighbor > centerPix) << (numNeighbors - n - 1);
}
}
}
//进行旋转不变处理
for (int i = 0; i < RLBPImage.rows; i++)
{
for (int j = 0; j < RLBPImage.cols; j++)
{
uchar currentValue = RLBPImage.at(i, j);
unsigned char minValue = currentValue;
for (int k = 1; k < numNeighbors; k++)
{
//循环左移
unsigned char temp = (currentValue >> (numNeighbors - k)) | (currentValue << k);
if (temp < minValue)
{
minValue = temp;
}
}
RLBPImage.at(i, j) = minValue;
}
}
imshow(output_iamge1, RLBPImage);
} 测试效果:
Harr-Like特征提取
Haar-like是一种非常经典的特征提取算法,尤其是它与AdaBoost组合使用时对人脸检测有着不错的效果,虽然只是在当时而言。OpenCV也对AdaBoost与Haar-like组成的级联人脸检测做了封装,所以一般提及Haar-like的时候,一般都会和AdaBoost,级联分类器,人脸检测,积分图等等一同出现。但是Haar-like本质上只是一种特征提取算法,下面我们只从特征提取的角度聊一聊Haar-like。
最原始的Haar-like特征在2002年的《A general framework for object detection》提出,后来Paul Viola和Michal Jones提出利用积分图像法快速计算Haar特征的方法(《Rapid object detection using a boosted cascade of simple features》)。之后,Rainer Lienhart 和 Jochen Maydt用对角特征对Haar特征库进行了扩展(《An extended set of Haar-like features for rapid object detection》)。
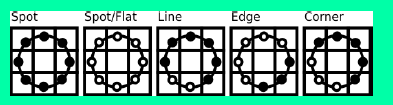
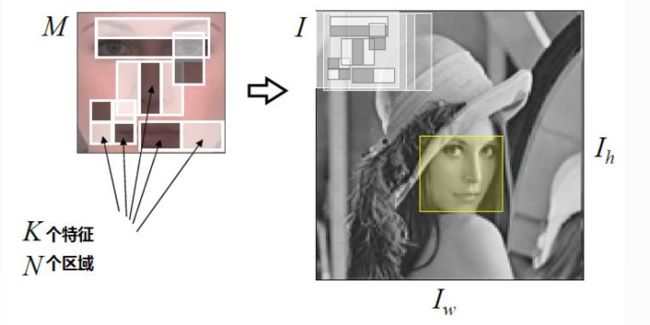
如上图所示的矩形特征,表现了人脸眼睛周围的特征,眼睛区域的颜色比脸颊区域的颜色深,同样,其他目标,也可以用一些矩形特征来表示。使用特征比单纯地使用像素点具有很大的优越性,并且速度更快。
在给定有限的数据情况下,基于特征的检测能够编码特定区域的状态,而且基于特征的系统比基于像素的系统要快得多。矩形特征对一些简单的图形结构,比如边缘、线段,比较敏感,但是其只能描述特定走向(水平、垂直、对角)的结构,因此比较粗略。如上图,脸部一些特征能够由矩形特征简单地描绘,例如,通常,眼睛要比脸颊颜色更深;鼻梁两侧要比鼻梁颜色要深;嘴巴要比周围颜色更深。
特征检测器的大小不固定,可以是2x2,4x4,8x8,16x16,24x24等等。对于一个 24×24 检测器,其内的矩形特征数量超过160,000 个,必须通过特定算法甄选合适的矩形特征,并将其组合成强分类器才能检测人脸。
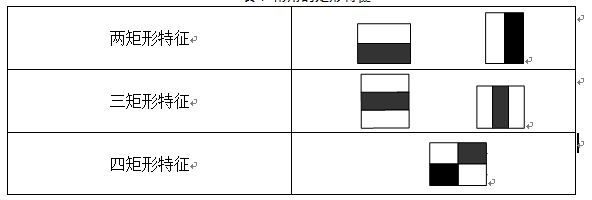
常用的矩形特征有三种:两矩形特征、三矩形特征、四矩形特征,如图:
由图表可以看出,两矩形特征反映的是边缘特征,三矩形特征反映的是线性特征、四矩形特征反映的是特定方向特征。
特征模板的特征值定义为:白色矩形像素和减去黑色矩形像素和,如第一个图右边所示。接下来,要解决两个问题,1:求出每个待检测子窗口中的特征个数。2:求出每个特征的特征值。
子窗口中的特征个数即为特征矩形的个数。训练时,将每一个特征在训练图像子窗口中进行滑动计算,获取各个位置的各类矩形特征。在子窗口中位于不同位置的同一类型矩形特征,属于不同的特征。可以证明,在确定了特征的形式之后,矩形特征的数量只与子窗口的大小有关。在24×24的检测窗口中,矩形特征的数量约为160,000个。特征模板可以在子窗口内以“任意”尺寸“任意”放置,每一种形态称为一个特征。
如图所示的一个m*m大小的子窗口,可以计算在这么大的子窗口内存在多少个矩形特征。
以 m×m 像素分辨率的检测器为例,其内部存在的满足特定条件的所有矩形的总数可以这样计算:对于 m×m 子窗口,我们只需要确定了矩形左上顶点A(x1,y1)和右下顶点B(x2,y2) ,即可以确定一个矩形;如果这个矩形还必须满足下面两个条件(称为(s, t)条件,满足(s, t)条件的矩形称为条件矩形):
- x 方向边长必须能被自然数s 整除(能均等分成s 段);
- y 方向边长必须能被自然数t 整除(能均等分成t 段);
则这个矩形的最小尺寸为s×t 或t×s, 最大尺寸为[m/s]·s×[m/t]·t 或[m/t]·t×[m/s]·s;其中[ ]为取整运算符。
我们通过下面两步就可以定位一个满足条件的矩形:
由上分析可知,在m×m 子窗口中,满足(s, t)条件的所有矩形的数量为:
实际上,(s, t)条件描述了矩形特征的特征,下面列出了不同矩形特征对应的(s, t)条件:
下面以 24×24 子窗口为例,具体计算其特征总数量:
上面只列举了基本结构的矩形特征,其实还存在其他很多不同的特征,如下所示:
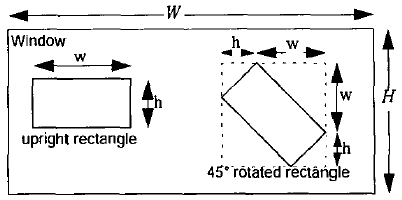
对于45°的rotated特征(如1(c)和1(d)),w,h表示如下图所示:
其计算公式为:
首先有两点要清楚:
1、对于某特定大小的特征,在窗口内滑动计算。
也就是如图1(a)特征大小为2*1,对于24*24的图像。水平可滑动23步,垂直滑动24步,所以共有23*24个特征。
2、对于一个特征,特征本身沿水平、竖直方向分别缩放。
还看特征1(a),特征大小为2*1,则延水平方向可放大为:4*1,6*1,8*1,…,24*1;竖直方向可放大为:2*1,2*2,2*3,…,2*24。即每个特征有XY种放大方式。(!放大的矩形特征并限制保持2:1的比例!)
Harr检测示意图如下:
维度计算:
我们知道了Harr特征的计算过程,它的维度就很好计算出来了。 Haar的总维度应该是每一种窗口产生的维度的和; 而每一种窗口产生的维度又是它遍历所有比例之后的维度和; 一个窗口固定一个比例时的维度就是滑动遍历整个图像所产生的维度和。
小结
终于说完了三个最基础的图像特征提取的方法,欢迎各位大佬评论留言转发,谢谢!