机器学习之线性回归及代码示例

一、线性回归

线性回归一般用来做连续值的预测，预测的结果为一个连续值。因训练时学习样本不仅要提供学习的特征向量X，而且还要提供样本的实际结果（标记label），所以它是一种有监督学习。其中 X={x0,x1,...,xn} 。

线性回归需要学习得到的是一个映射关系 f：X→y ，即当给定新的待预测样本时，我们可以通过这个映射关系得到一个测试样本 X 的预测值 y 。

在线性回归中，假定输入X和输出y之间具有线性相关的关系。
例如当特征向量 X 中只有一个特征时，需要学习到的函数应该是一个一元线性函数 y=a+bx 。

当情况复杂时，考虑 X 存在n个特征的情形下，我们往往需要得到更多地系数。我们将 X 到 y 的映射函数记作函数 hθ(X) ：

hθ(X)=∑i=0nθixi=θTX

其中，为了在映射函数hΘ(X)中保留常数项，令 x0 为1，所以特征向量 X={1,x1,x2,...,xn} ，特征系数向量 θ={θ0,θ1,θ2,...,θn} 。

当给定一个训练集数据的情况，可以通过某个算法，学习出来一个线性的映射函数 hθ(X) 来求得预测值 y 。

二、损失函数

在需要通过学习得到的映射函数 hθ(X) 中，需要通过训练集得到特征系数向量 θ={θ0,θ1,θ2,...,θn} 。

那怎么得到所需的特征系数向量？怎么保证得到的特征系数向量是足够好？这里会有一个评判标准：损失函数。

根据特征向量系数 θ ，可有损失函数 J(θ) 如下 :

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2

其中 hθ(X) 为需要学习到的函数， m 为训练集样本的个数， Xi 表示训练集中第 i 个样本的特征向量， yi 表示第 i 个样本中的标签。

为了得到预测值 hθ(Xi) 和 yi 的绝对值，在公式上使用了平方数。为了平均每个样本的损失，在公式上对损失和进行除以 m 操作，，再除以 2 是为了之后的求导计算。

三、梯度下降算法求解

批量随机梯度下降BGD

在上面，找到了一个特征系数向量 θ 好坏的损失函数 J(θ) 。为了迎合这样的评判标准得到较好的 θ ，需对损失函数值进行最小化，即让损失函数在样本中的损失最小。

对于损失函数 J(θ) ，可以发现 θ 是一个关于 \theta 的凸函数。

梯度下降就是一个不断地最小化损失函数的过程。从图像上来看，先初始化 θi 为某个值，然后让 θi 沿着J J(θ) 在 θi 的偏导方向不断地走，直达走到底部收敛为止，最后就可以得到 J(θ) 最小时的那个 θi 的值。

这个不断迭代的过程犹如一个不断下山的过程，我们可以得到图中关于 θi 的迭代函数，其中 α 为每次下山的步长。

当 θi 小于最低处的值的时，对其的偏导为负，在迭代过程中， θi 不断地增大以逼近最低处的值；当 θi 大于最低处的值时，对其的偏导为正， θi 会不断地做减法以逼近最低处的值。所以当步长 α 较小时， θi 会收敛于最低处的值。通常，我们将 α 叫做学习率 （learning rate）。

对于特征向量系数 θ 中的每个元素 θi ，可以通过上面的迭代公式，它们都会往各自偏导的方向“下山”，“下山”的方向（梯度）为偏导的方向，按照这样的下山方向，下山的速度会更快一点。梯度下降算法就是这么的一个“下山”的过程。

对下山迭代公式进行展开，可得到具体求得 θi 的公式：

其中， x(i)0 为第 i 个训练样本的第 0 个特征值，为保持 hθ(X) 的常数项，通常令 x(i)0 为1。 hθ(X) 为在迭代过程中通过 θ 得到的预测函数，它的表达式会跟随着 θ 的变化而不断地变化。

当学习率 α 很小时，我们往往需要迭代更多次才可以“下山”达到山底， θ 收敛很慢；当学习率a很大时，“下山”步子迈大后，往往会在山底的两边跳跃，可能无法到达山底， θ 会出现震荡，导致无法收敛。
一般情况下， α 可设为0.01，0.005等，也可以在迭代的过程中不断自适应地修改 α 的值，例如可以在迭代过程中不断地减小 α 的值。

其他梯度下降算法

a. 批量梯度下降算法BGD中， θi 的更新要用到所有的样本数，需要计算所有样本汇总的误差来进行梯度下降：

θi=θi−α1m∑i=1m(hθ(X(i))−y(i))X(i)j

这样训练速度会随着样本数量 m 的增加而变得缓慢。

b. 随机梯度下降法SGD：利用每个样本的损失函数对 θi 求偏导得到对应的梯度，来更新 θi 的值，每次计算一个样本的误差来进行梯度下降：

for  i=1  to  m：θi=θi−α(hθ(X(i))−y(i))X(i)j

随机梯度下降算法通过每个样本来迭代更新一次，当一些训练样本为噪声样本时，会导致SGD并不是向着整体最优化方向迭代。因此SGD算法在解空间的搜索比较盲目，但在大体上是往着最优值方向移动的。

c. 小批量梯度下降法MBGD：MBGD是前面两个算法SGD和BGD的一个折中，既要保证算法的计算速度，又要保证参数训练的最优性，每次需要计算一小批量样本的汇总误差来进行梯度下降。MBGD对 θi 的迭代如下所示：

for  k=0,10,20,...,90：θi=θi−α110∑i=kk+9(hθ(X(i))−y(i))X(i)j

上式设置的一个batch大小为 10 个训练样本，不同的任务所设置的batch大小也有所不同，可把 batch的大小可看一个超参数。

梯度下降的注意

在使用梯度下降求解最优化的解时，要注意对特征进行归一化，这样可以提升模型的收敛速度。考虑两维的情况：假如样本只有两个特征时，一个特征取值于 100 到 1000 之间，另一个特征取值于0到1之间，可在 (θ1,θ2) 平面上可以画出目标函数的等高线：

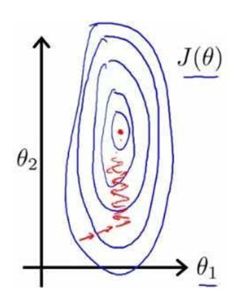
可得到一个个窄长的类椭圆等高线，导致在梯度下降时不断地走“之”路线，增长了迭代时间。

若对特征进行归一化后，每个特征之间具有相近的尺度，在 (θ1,θ2) 平面得到的是类圆等高线，梯度下降方向直指圆心，可帮助梯度下降算法更快地收敛。

四、过渡到多项式回归

通过上面的线性回归，我们可以得到一个线性的映射函数 hθ(X) ：

hθ(X)=∑i=0nθixi=θTX

对于 x1,x2,...,xn 这些特征，可以使用 多项式特征 的方法，将多个特征进行组合，得到多次项的特征。

这样一来， hθ(X) 依然还是个线性函数，不过与之线性的不是原本的特征，而是与 多项式特征和原来的特征 线性相关。通过这样的方法，可将线性回归过渡到多项式回归，不过这样做同时也会导致特征的维度变高，也会增加一些没必要的特征。

五、过拟合的正则化

当我们的损失函数 J(θ) 在样本中损失较大时，会出现欠拟合的情况，即对样本的预测值和样本的实际结果值由较大的差距。

当我们的损失函数 J(θ) 在样本中损失约等于0 时，这时 hθ(X) 图像穿过样本的每一个点，这样会出现过拟合的情况，缺乏泛化能力，函数波动比较大，对待预测的样本预测能力比较弱。

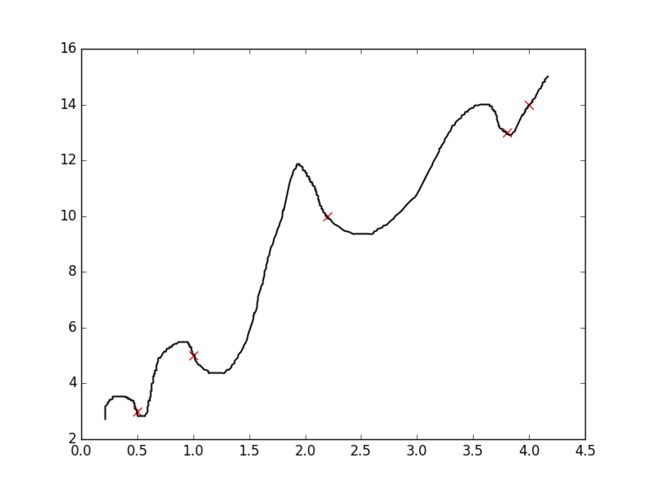
对于过拟合问题，可以使用 正则化 的方法，即在原来的损失函数 J(θ) 上加上一个“尾巴”:

无正则化时的损失函数：

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2

L1正则化下的损失函数：

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2+λ||θ||1

||θ||1=∑θi

L2正则化下的损失函数：

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2+λ||θ||22

||θ||2=∑θ2i−−−−−√

L1正则化、L2正则化也称为Lasso正则化、Ridge正则化，其中 λ 为模型的超参数。

正则化后的损失函数不仅要最小化预测值与样本点实际值间的差距了，还得最小化参数向量 θ 。当 hθ(X) 函数图像穿过所有样本点时，函数图像波动会非常大，（平方项、立方项等高次项的）的权重 θi 会很大，这样便会导致它的损失函数并非最小的。

正则化后，不仅要求 hθ(X) 接近更多的点，还要控制（高次项的） θi 值，使得控制函数不能波动太大，而且正则化之后损失函数无法等于0。

L1正则化往往会使得一些 θi 值趋近于0（这可用于特征的选择），L2正则化往往会使得 θi 值之间差别不会太大， θi 值之间的变化比较稳定。

六、最小二乘法求解

根据特征向量系数 θ ，可有损失函数 J(θ) 的矩阵表示 如下 :

J(θ)=12m∑i=1m(X(i)θ−y(i))2=12m(Xθ−Y)T(Xθ−Y)

其中 X 为 m×n 的矩阵， Y 为 m×1 的矩阵， θ 为长度为 n 的列向量， m 为训练样本的个数， n 为样本的特征维度，需要计算得到的 θ 为：

θ=argminθJ(θ)

由最小二乘法，令 J(θ) 对向量 θ 的一阶导数为零：

∂J(θ)∂θ=1mXT(Xθ−Y)=0

因此可得： XTXθ=XTY ，其中 XTX 是一个 n×n 的矩阵，当 XTX 可逆时，可通过公式得到

θ=(XTX)−1XTY

当 XTX 可逆时， XTX 须为满秩（秩 为 n）。

X 为 m×n 的矩阵，其秩为 m 和 n 中最小的一个数，为保证 XTX 满秩， m 需大于 n ，即训练样本的个数需大于样本的特征维度。

上述的 XTX 不一定是可逆的，而当 J(θ) 加上正则化项之后：

J(θ)=12m∑i=1m(hθ(X(i))−y(i))2+λ||θ||22

由最小二乘法，令 J(θ) 对 θ 的一阶导数为零：

∂J(θ)∂θ=1mXT(Xθ−Y)+2λθ=0

可得到

θ=(XTX+2λI)−1XTY

其中 I 为单位矩阵，因 XTX 为半正定矩阵，而 2λI 为正定矩阵，因此 XTX+2λI 为正定矩阵，总是可以求得其逆 (XTX+2λI)−1 ，可以通过式子得到 θ 的值。

七、代码示例

• 在sklearn的房价数据上使用线性回归，多项式回归：

from sklearn import datasets

boston = datasets.load_boston() # 加载房价数据
X = boston.data
y = boston.target
print X.shape
print y.shape

(506L, 13L)
(506L,)

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y ,test_size = 1/3.,random_state = 8)

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

# 线性回归
lr = LinearRegression(normalize=True,n_jobs=2) 
scores = cross_val_score(lr,X_train,y_train,cv=10,scoring='neg_mean_squared_error') #计算均方误差
print scores.mean()

lr.fit(X_train,y_train)
lr.score(X_test,y_test)

-24.4294227766

0.6922002690740765

from sklearn.preprocessing import PolynomialFeatures

# 多项式回归

for k in range(1,4):
    lr_featurizer = PolynomialFeatures(degree=k) # 用于产生多项式 degree:最高次项的次数
    print '-----%d-----' % k

    X_pf_train = lr_featurizer.fit_transform(X_train)
    X_pf_test = lr_featurizer.transform(X_test)

    pf_scores = cross_val_score(lr,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print pf_scores.mean()

    lr.fit(X_pf_train,y_train)
    print lr.score(X_pf_test,y_test)
    print lr.score(X_pf_train,y_train)

-----1-----
-24.4294227766
0.692200269074
0.755769163218
-----2-----
-22.7848754621
0.833095620158
0.93821030015
-----3-----
-6325.76073853
-16.550355583
1.0

当 k=1 时，回归为线性回归；当 k=2 时，回归为多项式回归，模型的效果比线性回归要好一点。
当 k=3 时，已经出现过拟合现象，模型在训练集上得分很高，然而在验证集上得分很低，从交叉验证的得分结果也可以看得出来

# 正则化解决k=3的过拟合现象

lr_featurizer = PolynomialFeatures(degree=3) # 用于产生多项式 degree:最高次项的次数
X_pf_train = lr_featurizer.fit_transform(X_train)
X_pf_test = lr_featurizer.transform(X_test)

# LASSO回归：
from sklearn.linear_model import Lasso

for a in range(0,0.0005）:
    print '----%f-----'% a
    lasso = Lasso(alpha=a,normalize=True)
    pf_scores = cross_val_score(lasso,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print pf_scores.mean()

    lasso.fit(X_pf_train,y_train)
    print lasso.score(X_pf_test,y_test)
    print lasso.score(X_pf_train,y_train)

----0.000000-----
-29.3011407539


D:\Users\cxm\Anaconda2\lib\site-packages\ipykernel\__main__.py:15: UserWarning: With alpha=0, this algorithm does not converge well. You are advised to use the LinearRegression estimator


0.768272379891
0.965488575704
----0.000500-----
-11.2829107107
0.837992634283
0.943520416421

对比 alpha=0 和 alpha = 0.0005的情况，发现Lasso正则化处理后，模型的评价会提高很多。

# 正则化解决k=3的过拟合现象

lr_featurizer = PolynomialFeatures(degree=3) # 用于产生多项式 degree:最高次项的次数
X_pf_train = lr_featurizer.fit_transform(X_train)
X_pf_test = lr_featurizer.transform(X_test)

from sklearn.linear_model import Ridge

# 岭回归
for a in [0,0.005]:
    print '----%f-----'% a
    ridge = Ridge(alpha=a,normalize=True)
    pf_scores = cross_val_score(ridge,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print pf_scores.mean()

    ridge.fit(X_pf_train,y_train)
    print ridge.score(X_pf_test,y_test)
    print ridge.score(X_pf_train,y_train)

----0.000000-----
-6143.74385842
-16.4626220878
1.0
----0.005000-----
-14.0438948376
0.823709164706
0.948990485145

对比 alpha=0 和 alpha = 0.0005的情况，发现Ridge正则化处理后，模型的评价会提高很多。

• tensorflow实现正则化解决过拟合现象

from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error

X_data = load_boston().data
Y_data = load_boston().target.reshape(-1,1)

print (X_data.shape,Y_data.shape)

((506, 13), (506, 1))

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_data, Y_data ,test_size = 1/3.,random_state = 8)

from sklearn.preprocessing import PolynomialFeatures

pl_featurizer = PolynomialFeatures(degree=2) # 用于产生多项式 degree:最高次项的次数

X_train = pl_featurizer.fit_transform(X_train)
X_test = pl_featurizer.transform(X_test)

print X_train.shape

(337, 105)

import tensorflow as tf

X = tf.placeholder(tf.float32,[None,105])
Y = tf.placeholder(tf.float32,[None,1])

tf_W_L1 = tf.Variable(tf.zeros([105,1]))
tf_b_L1 = tf.Variable(tf.zeros([1,1]))

pred = tf.matmul(X,tf_W_L1)+tf_b_L1
print pred

Tensor("add_6:0", shape=(?, 1), dtype=float32)

# L1正则化：
loss = tf.reduce_mean(tf.pow(pred-Y,2))*0.5 +0.001*tf.reduce_sum(tf_W_L1)

train_step = tf.train.AdamOptimizer(0.01).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(20000):
        sess.run(train_step,feed_dict={X:X_train,Y: y_train})
        if(i%10000==0):
            print mean_squared_error(y_train,pred.eval(feed_dict={X:X_train}).flatten().reshape(-1,1))
    print 'test mse: '
    print mean_squared_error(y_test,pred.eval(feed_dict={X:X_test}).flatten().reshape(-1,1))

42669456.628
10.4569020596
test mse: 
15.7365063927