2.6

今天是数学归纳+递推，考的还可以, A了3道题, 最后一题树上的点分治没有学过，本来可以得至少40分的暴力分，但爆空间，0分
预计得分：340；实际得分300，rank 2
因为除开最后一道题，基本都是数学题，所以写的比较好?!
今天的题目不难，，，再加努力(特别是图论部分)！！！

目录

古代人的难题

考试的时候就A了，，，
做题的时候可以考虑写一个搜索，从k = 1,时开始找规律，不难发现是斐波那契数列
具体证明如下：

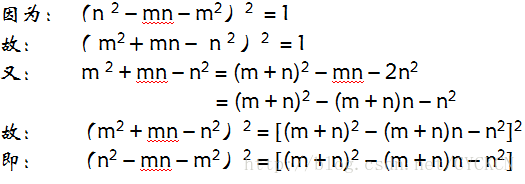
不妨设存在解集(x, y), 又推导可知必存在解集(x + y, x),故满足斐波拉契数列，得证；

#include 
#include 
#include 
#include 
#include 
#define LL long long
using namespace std;

LL k, f[100];

int main() {
//  freopen("puz.in", "r", stdin);
//  freopen("puz.out", "w", stdout);
    scanf("%lld", &k);
    f[1] = 1, f[2] = 1;
    for (int i = 3; i <= 100; ++i) {
        f[i] = f[i - 1] + f[i - 2];
        if (f[i] > k) {
            printf("%lld %lld\n", f[i - 1], f[i - 2]); return 0;
        }
    }
}

化学反应

考试的时候A了……
本来看到这道题是一脸懵逼，于是非常无辜的写了一个O(n^2)的搜索
考试还剩半个小时的时候，想了想又加了个剪枝，于是就A了……
显然对于每一个元素的b值，仅当他相对于另一个选择元素最大时才会对ans产生影响，故想到枚举每个元素的b值为max是的情况
可是，显然如果要找到对于当前元素最小的a，仍然需要一个for循环，并没有优化，故想到以a值为基础进行排序，这样便可以在找到与之a值的差最小的元素的同时，使b[i]最大
我相信你们没有看懂，我自己也没有太看懂我写的东西，直接放代码吧……

#include 
#include 
#include 
#include 
#include 
using namespace std;

struct node{
    long long a, b;
} ele[100000 + 10];
long long n, ans, T;
bool flag = 0;

inline bool comp (node x, node y) { return x.a > y.a;}

int main() {
//  freopen("reaction.in", "r", stdin);
//  freopen("reaction.out", "w", stdout);
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i) 
            scanf("%lld %lld", &ele[i].a, &ele[i].b);
        sort(ele + 1, ele + 1 + n, comp);
        for (int i = 1; i <= n; ++i) {
            int la = i - 1, lb = i + 1;
            long long dis;
            while (la >= 1 && ele[la].b > ele[i].b) la--;
            while (lb <= n && ele[lb].b > ele[i].b) lb++;
            if (la < 1 && lb > n) continue;
            else if (la < 1) dis = abs(ele[lb].a - ele[i].a);
            else if (lb > n) dis = abs(ele[i].a - ele[la].a);
            dis = min(abs(ele[lb].a - ele[i].a), abs(ele[i].a - ele[la].a));
            dis++;
            if (!flag) ans = dis * ele[i].b, flag = 1;
            else ans = min(ans, dis * ele[i].b);
        }
        printf("%lld\n", ans);
        flag = 0, ans = 0;
        memset(ele, 0, sizeof(ele));
    }
    return 0;
}

巧克力

考试的数据并没有出来，所以在vijos上找了另一道题，不同的使vijos是多组数据，最后因为scanf T了3个点，改成cin就A了??!
思路很简单，显然竖着切一下，对以后竖着切没有影响，反而在那之后横着切的都要多切一刀，所以显然会先切代价大的，同时记录该种切法对另一种切法的影响，再将该代价变化为受影响后的代价放入ans即可

---

这是考试的代码,即一组数据

#include 
#include 
#include 
#include 
#include 
using namespace std;

long long ans = 0;
int n, m, cnta = 1, cntb = 1;
long long a[100000 + 10], b[100000 + 10];

inline bool comp(long long x, long long y) {
    return x > y;
}

int main() {
    freopen("chocolate.in", "r", stdin);
    freopen("chocolate.out", "w", stdout);
    scanf("%d %d", &n, &m);
    for (int i = 1; i < n; ++i) cin >> a[i];
    for (int i = 1; i < m; ++i) cin >> b[i];
    sort(a + 1, a + n, comp);
    sort(b + 1, b + m, comp);
    int la = 1, lb = 1;
    while(la < n || lb < m) {
        if (a[la] < b[lb])  ans += b[lb] * cntb, cnta++, lb++;
        else ans += a[la] * cnta, cntb++, la++;
    }
    printf("%lld\n", ans);
    return 0;
}

---

vijos的代码，即多组数据

#include 
#include 
#include 
#include 
#include 
using namespace std;

long long ans = 0;
int n, m, cnta = 1, cntb = 1, T;
long long a[100000 + 10], b[100000 + 10];

inline bool comp(long long x, long long y) {
    return x > y;
}

int main() {
    freopen("chocolate.in", "r", stdin);
    freopen("chocolate.out", "w", stdout);
    scanf("%d", &T);
    while(T--) {
        ans = 0;
        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));
        scanf("%d %d", &n, &m);
        for (int i = 1; i < n; ++i) cin >> a[i];
        for (int i = 1; i < m; ++i) cin >> b[i];
        sort(a + 1, a + n, comp);
        sort(b + 1, b + m, comp);
        int la = 1, lb = 1;
        while(la < n || lb < m) {
            if (a[la] < b[lb])  ans += b[lb] * cntb, cnta++, lb++;
            else ans += a[la] * cnta, cntb++, la++;
        }
        printf("%lld\n", ans);
        cnta = 1, cntb = 1;
    }
    return 0;
}

树上的点对

唯一一道没有A的题，0分，大概因为它是图论，不是数论吧……
参考的黄学长的代码，详情可参考2009年漆子超的论文例一
代码中赋有自己的理解，不知道对不对啊…………

#include 
#include 
#include 
#include 
#include 
#define inf 0x7fffffff
using namespace std;

int n, k, a, b, c;
int cnt,sum,ans,root;
int head[10005],deep[10005],d[10005],f[10005],son[10005];
bool vis[10005];
struct node {
    int to, next, v;
} e[20005];

inline void add(int a, int b, int c) {
    e[++cnt].next = head[a];
    e[cnt].to = b;
    e[cnt].v = c;
    head[a] = cnt;
}

inline void findfa(int x, int fa) {//寻找树的重心 
    son[x] = 1, f[x] = 0; //son为儿子个数,f为x的子数的大小 
    for (int i = head[x]; i; i = e[i].next) {
        if (e[i].to == fa || vis[e[i].to]) continue;
        findfa(e[i].to, x);
        son[x] += son[e[i].to]; //更新儿子个数 
        f[x] = max(f[x], son[e[i].to]); //更新子树大小 
    }
    f[x] = max(f[x], sum - son[x]); //使之子树最大 
    if (f[x] < f[root]) root = x; //重心是子树大小最小的点-->找重心 
}

inline void getdeep(int x, int fa) {//更新该节点到其爸爸的距离 
    deep[++deep[0]] = d[x]; //赋上已有距离 
    for (int i = head[x]; i; i = e[i].next) {
        if (e[i].to == fa || vis[e[i].to]) continue;
        d[e[i].to] = d[x] + e[i].v; //用已有距离更新 
        getdeep(e[i].to, x); //递归调用 
    }
}

inline int cal(int x, int now) { //以x为根节点，已有路径长度为now 
    d[x] = now; deep[0] = 0;  
    getdeep(x, 0); //更新以x为根节点的子树到x节点的距离 
    sort(deep + 1, deep + deep[0] + 1);  
    int t = 0, l, r;
    for (l = 1, r = deep[0]; l < r;) {
        if (deep[l] + deep[r] <= k) t += (r - l), l++; //在树上跳着找合法点对 
        else r--;
    }
    return t;
}

inline void work(int x) { //统计以x为根节点的字数合法数对的个数 
    ans += cal(x, 0); //以x为根节点，所以 d为0 
    vis[x] = 1;
    for (int i = head[x]; i; i = e[i].next) {
        if (vis[e[i].to]) continue;
        ans -= cal(e[i].to, e[i].v); //减去x的每一个子树中合法数对的个数 
        sum = son[e[i].to]; //更新以x的子节点为根节点的树的节点个数 
        root = 0;  
        findfa(e[i].to, root); //找以e[i].to为根节点的子树的重心 
        work(root); //递归调用 
    }
}

int main() {
    while(scanf("%d %d", &n, &k) && n != 0 && k != 0) {
        ans = root = cnt = 0;
        memset(vis, 0, sizeof(vis));
        memset(head, 0, sizeof(head));
        for (int i = 1; i < n; ++i) scanf("%d %d %d", &a, &b, &c), add(a, b, c), add(b, a, c);
        sum = n, f[0] = inf;
        findfa(1, 0);
        work(root);
        printf("%d\n", ans);
    }
    return 0;
}