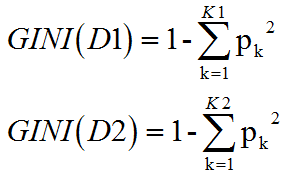机器学习之决策树--CART
一、什么是CART决策树
决策树概念:机器学习之决策树–原理分析
CART(Classification And Regression Tree),即分类与回归树。
由它的名字可以发现,它分为分类树和回归树两种。
分类树就是决策树传统做的事情,ID3和C4.5就是做这个事情。那CART分类树和它们的区别是什么呢?ID3和C4.5是多分支的,而CART规定每个内部节点只能是二分的。其他过程和C4.5类似,同样可以做数值型属性的划分。
回归树的目标类别不是离散型的分类,而是连续型的数值。CART在做回归时,根据叶子节点的类型是具体数值还是其他的机器学习模型又可以分为回归树和模型树。回归时,通过一系列的属性划分,将样本划分为多个群落,群落之间有鲜明的区别,既是一系列属性间的区别。如果是回归树,则每个群落的均值或其他的代表性指标作为该群落的回归值。如果是模型树,则每个群落内部通过其他的机器学习模型进行拟合,最后根据属性选择,做出最后的预测。因为经过属性划分之后,形成了多个群落,其实这些群落也就是类别,所以回归树和模型树既算回归,也称得上分类。
可以总结CART和C4.5的区别:
- CART的所有内部节点都是二分的
- CART选择GINI指数作为特征选择标准
二、什么是GINI指数?
GINI指数是一种不等性度量,是一个介于0~1之间的数,0表示单一类别,1表示最平均的状态,所以内部包含的类别越多,GINI指数越大。
以某个样本集合D为例,其中共有K个类别的样本,pk为第k类样本数占集合D样本数的比例,即第k类出现的概率,则其GINI指数计算公式为
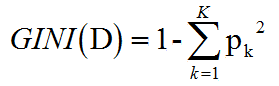
三、如何通过GINI指数选择切分特征?
当一个样本被划分为两部分时,分别计算这两个部分的GINI指数,然后通过这两部分的比例,用类似信息增益的方式,求出GINI增益
假设一个样本D被划分成D1和D2两个部分。则两个部分的GINI指数可以如下求出
有了两个部分的GINI指数,则可以求出GINI增益。
计算出所有特征的GINI增益之后,选择GINI增益最小的那个作为划分特征。因为其代表了最小的混乱度
四、如果某个特征的类别数大于2怎么办?
因CART要求树是二分的,那当某个特征的类别大于2时,就需要处理。
这里有一个“双化”的概念,即当类别数大于2时,要将其用“是XX”和“不是XX”进行处理,取GINI增益最小的那个划分情况作为该属性的划分。
当某个特征是经过双化之后的划分,则对“不是XX”中的属性,在接下来的划分中仍然需要进行处理。
五、CART分类树
CART分类树可以参照 C4.5分类树。因CART要求二分,所以每次划分,若是类别型数据,则需要先进行双化处理,若是数值型属性,则和C4.5一样,用≤θ和>θ划分为两个子集。只是在所有的处理中,都是选择GINI增益最小的特征进行划分。在本文中不举例,读者可参照 机器学习之决策树–C4.5 中的例子,自行进行模拟。
六、CART回归树
回归树即指最终的预测结果是一个连续型的数值,而不是分类。其实,将数值看做类别,也就是分类。
回归树在特征选择的判断依据上,和分类树不同,不是用GINI指数,而是用残差平方和。
每次划分都会将当前节点划分为两部分,则两部分的所有样本都有自己的数值结果,则需要对每个部分的数值结果集进行求残差平方和的方法,选择两部分的加权残差平方和最小的那个划分特征作为当前节点的划分特征。
最后的叶子节点,即表示回归结果,其实是对叶子节点上的所有样本的数值结果集求平均值的方式,以平均值代表该叶子节点的回归结果。
七、CART回归树举例
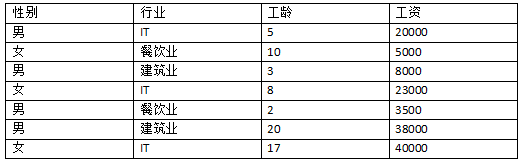
我乱写一个数据集来做举例
1.以性别为特征进行划分,计算加权残差平方和
性别共男、女两个取值。男性共4个样本,工资均值为17375,残差平方和为712687500,女性共3个样本,工资均值为22666.67,残差平方和为612666666.7。
以性别为特征划分的加权残差平方和为 t(性别) = (4/7)*712687500 + (3/7)*612666666.7 = 669821428.6
2.以行业为特征进行划分,计算加权残差平方和
行业共IT、餐饮业、建筑业三个取值。故需要双化。
- 以“是IT”和“不是IT”进行划分。“是IT”共3个样本,工资均值为27666.67,残差平方和为232666666.7,“不是IT”共4个样本,工资均值为13625,残差平方和为802687500。以“IT”为特征划分的加权残差平方和为 t(IT) = (3/7)*232666666.7 + (4/7)*802687500 = 558392857.2
- 以“是餐饮业”和“不是餐饮业”进行划分。“是餐饮业”共2个样本,工资均值为4250,残差平方和为1125000.00,“不是餐饮业”共5个样本,工资均值为25800,残差平方和为708800000。以“餐饮业”为特征划分的加权残差平方和为 t(餐饮业) = (2/7)*1125000.00 + (5/7)*708800000 = 506607142.9
- 以“是建筑业”和“不是建筑业”进行划分。“是建筑业”共2个样本,工资均值为23000,残差平方和为450000000,“不是建筑业”共5个样本,工资均值为18300,残差平方和为891800000。以“建筑业”为特征划分的加权残差平方和为 t(建筑业) = (2/7)*450000000 + (5/7)*891800000 = 765571428.6
所以以行业为特征进行划分的最小残差平方和是506607142.9
3.以工龄为特征进行划分,计算加权残差平方和
工龄是一个连续型的数值特征,所以要用≤θ和>θ划分为两个子集。数值型特征的划分方式参照 机器学习之决策树–C4.5 例子中年龄的划分方式,但是以残差平方和最小作为选择依据。
先将工龄排序,然后以中间数进行切分,求残差平方和,以最小的那个为切分。
可以求得当以工龄 10 和 17 的 中间数13.5做切分时,残差平方和最小,为230714285.7。
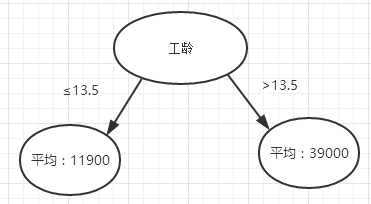
4.经过一次计算,可见以工龄选取13.5做切分值时,目标数据集的残差平方和最小,故第一次切分选择工龄为切分特征。可见下图。
5.回归树中非常重要的一点是参数的设置,即何时终结树的生长,让节点不再扩展。在此例中,右边的子节点中的样本数还有2个,但是其残差平方和已经非常小,如果再进行扩展,肯定会导致过拟合。故只对左边节点进行扩展。
根据我设定的一些终止条件,重复1-4步,最终可以生成这样一棵决策树。
八、CART模型树
模型树是在回归树的基础上的改进,其更加精确。
在回归树中,我们处理最后叶子节点的回归值时,采用均值来表示,显然这个不够精确。在模型树中,每个叶子节点上是一个机器学习模型,其中最简单的,就是线性回归模型。
线性回归模型树对叶子节点上的样本值进行线性回归,当新的数据进来时,根据线性回归模型,进行预测,这样更加准确。
九、思考:CART有哪些问题?优点是什么?
(一)CART可以做分类,也可以做回归和模型树,应用场景十分广泛。
(二)在做模型树时,回归方程显然需要自变量,自变量的选取如何做?
(三)在回归时,叶子节点上的数值如果是有偏的,则均值不能很好的反映情况,需要采取什么办法?