基于PCA模型的数据降维(复习13)
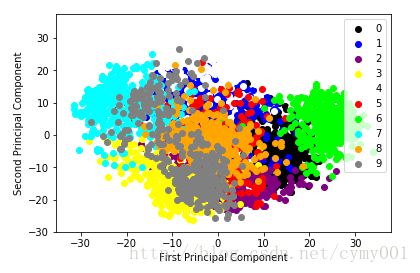
本文是个人学习笔记,内容主要基于PCA降维模型对手写体数据图像集进行降维,把原始64维度的数字图像压缩映射到二维空间,实验结果表明绝大多数数字之间仍然具有区分性。
在数据表现方面,无法用肉眼观测超过三个维度的特征。对于数据维度非常高的数据样本,通过无监督学习可以对数据进行降维,保留最具有区分性的低维度特征。在特征降维的方法中,主成分分析(Principal Component Analysis)是最为经典和实用的特征降维技术,特别在辅助图像识别方面有突出的表现。
特征降维形象点说就好比,矩阵中有两行是线性相关的,经过特征降维,只会保留其中一行;你要给一个三维盆栽拍照片,你可以从上下左右斜 45o 等角度拍二维照片,有的角度得到的信息多,更能表现原物体特征,但有的角度得到的信息就少。
利用PCA进行特征选择时,首先要把原来的的特征空间做了映射,使得新的映射后的特征空间数据彼此正交,这样做就尽可能保留下具备区分性的低维数据特征。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
digits_train=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra',header=None)
digits_test=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes',header=None)X_digits=digits_train[np.arange(64)] #从训练集中分离出特征和标签
y_digits=digits_train[64]from sklearn.decomposition import PCA
estimator=PCA(n_components=2)
X_pca=estimator.fit_transform(X_digits)from matplotlib import pyplot as plt
def plot_pca_scatter():
colors=['black','blue','purple','yellow','white','red','lime','cyan','orange','gray']
for i in range(len(colors)):
px=X_pca[:,0][y_digits.as_matrix()==i]
py=X_pca[:,1][y_digits.as_matrix()==i]
plt.scatter(px,py,c=colors[i])
plt.legend(np.arange(0,10).astype(str))
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()
plot_pca_scatter()下面针对digits数据集进行一组对比实验:(1)用原始64维度的像素特征,利用SVC对手写体数据图像进行识别分类;(2)用经过PCA压缩重建后的低维特征,利用SVC对手写体数据图像进行识别分类。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
digits_train=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra',header=None)
digits_test=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes',header=None)X_train=digits_train[np.arange(64)] #从训练集中分离出特征和标签
y_train=digits_train[64]
X_test=digits_test[np.arange(64)]
y_test=digits_test[64]from sklearn.svm import LinearSVC
svc=LinearSVC()
svc.fit(X_train,y_train)
y_predict=svc.predict(X_test)
estimator=PCA(n_components=20) #用PCA将原始64维图像数据压缩到20个正交的维度
pca_X_train=estimator.fit_transform(X_train)
pca_X_test=estimator.transform(X_test)
pca_svc=LinearSVC()
pca_svc.fit(pca_X_train,y_train)
pca_y_predict=pca_svc.predict(pca_X_test)from sklearn.metrics import classification_report
print(svc.score(X_test,y_test))
print(classification_report(y_test,y_predict,target_names=np.arange(10).astype(str)))
print(pca_svc.score(pca_X_test,y_test))
print(classification_report(y_test,pca_y_predict,target_names=np.arange(10).astype(str)))从上面的结果可见,经过PCA特征压缩和重建之后的特征数据会损失2%左右的预测准确性,但是相比原始数据64维的特征而言,使用PCA压缩降低了68.75%的维度。降维和压缩是选取数据中具有代表性的特征,在保持数据多样性的基础上,规避掉大量的特征冗余和噪声,不过这个过程也有可能会损失一些有用的模式信息。大量的实践表明,相较于损失的少部分模型性能,维度压缩能节省大量用于模型训练的时间,这样看PCA所带来的模型综合效率更为划算。