【算法导论】动态规划之“矩阵链乘法”问题
上一篇里,介绍了动态规划的“钢管切割”问题,这一次来看看“矩阵链乘法”。所谓矩阵链乘法就是一个或一个以上的矩阵连续相乘,这里主要关注的是乘法的次数。
一、概述
以两个矩阵相乘为例,A1*A2,A1和A2为两个矩阵,假设A1的行列数是p*q,A2的行列数是q*r。注意这里由于是A1乘以A2,所以A1的列数要等于A2的行数,否则无法做矩阵乘法,满足上述条件的矩阵,我们称之为“相容”的。那么对于A1*A2而言,我们需要分别执行p*r次对应A1的行元素乘以A2的列元素,根据线性代数知识,不难得出我们一共需要执行p*q*r次乘法。
对于两个矩阵相乘,一旦矩阵的大小确定下来了,那么所需执行的乘法次数就确定下来了。那么对于两个以上的矩阵呢?是不是也是这样呢。实际上,对于多个矩阵相乘,乘法执行的次数与“划分”有关。例如:
以矩阵链
①以((A1*A2)*A3)方式划分,乘法执行次数为:10*100*5+10*5*50=5000+2500=7500次
②以(A1*(A2*A3))方式划分,乘法执行次数为:100*5*50+10*100*50=25000+50000=75000次
我们可以发现,对于同样的矩阵链
二、如何获得最佳的矩阵链乘法划分和最少次数
其实这里与“钢管切割”有相似之处,在钢管切割问题中,我们使用一个一维数组来存储最佳收入,另一个一维数组来存储切割的划分处。
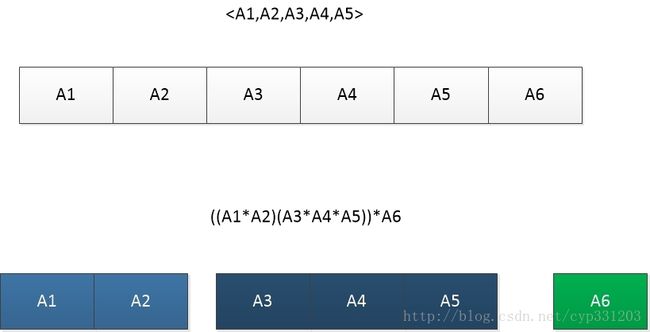
而这里,我们也可以将矩阵链看成一根要分割的“钢管”,只是这里记录的两个数组需要是二维的,因为我们需要记录的不仅是从哪里“断开”,还需要记录"每一段"到哪里截止。如下图:
使用一个长度为n+1的一维数组p来记录每个矩阵的规模,其中n为矩阵下标i的范围1~n,例如对于矩阵Ai而言,它的规模应该是p[i-1]到p[i]。由于i是从1到n取值,所以数组p的下标是从0到n。
用于存储最少乘法执行次数和最佳分段方式的结构是两个二维数组m和s,都是从1~n取值。m[i][j]记录矩阵链
需要注意的一点是当i=j时,m[i][j]=m[i][i]=0,因为一个矩阵不需要任何乘法。
假设矩阵链从Ai到Aj,有j-i+1个矩阵,我们从k处分开,将矩阵链分为Ai~Ak和Ak+1到Aj两块,那么我们可以比较容易的给出m[i][j]从k处分隔的公式:
m[i][j]=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
在一组确定的i和j值的情况下,要使m[i][j]的值最小,我们只要在所有的k取值中,i<=k
假设L为矩阵链的长度,那么L=j-i+1。当L=1时,只有一个矩阵,不需要计算。那么我们可以从L=2到n进行循环,对每个合理的i和j值的组合,遍历所有k值对应的m[i][j]值,将最小的一个记录下来,存储到m[i][j]中,并将对应的k存储到s[i][j]中,就得到了我们想要的结果。
根据上面的分析,不难给出过程的代码,注意这里也是使用的自底向上的方法,参看“钢管切割”:
//Ai矩阵的行列分别是p[i-1]和p[i],1<=i<=n
/*
* 求解最少次数的乘法括号划分方案
*/
void Matrix_Chain(int* p, int n, int** m, int** s) {
//①将对角线上的值先赋值为0
for (int i = 1; i <= n; i++) {
m[i][i] = 0;
}
int l = 0; //l为矩阵链的长度
//m[i][j]的第一个参数
int i = 0;
//m[i][j]的第二个参数
int j = 0;
int tmp = 0;
//②以长度L为划分,L从2开始到n
for (l = 2; l <= n; l++) {
//循环第一个参数,因为l的长度至少为2,所以i和j在这个循环里面肯定不相等
for (i = 1; i <= n - l + 1; i++) {
//因为j-i+1=l,所以j=l+i-1
j = i + l - 1;
//给m[i][j]赋初值,这里要寻找m[i][j]的最小值,本来应当给m[i][j]赋值一个正无穷,但是这里直接赋一个i=j时候的特值也可以
m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
//对于每个特定的i和j的组合,遍历此时所有的合适k值,k大于等于i小于j
for (int k = i + 1; k < j; k++) { //这里k不能等于j,因为后面要m[k+1][j],不然k+1就比j大了
tmp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (tmp < m[i][j]) {
m[i][j] = tmp;
s[i][j] = k;
}
}
}
}
} 经过上面的代码,我们就求得了每种i和j组合对应的最小乘法次数和对应的最佳分割处s[i][j]。
三、输出最优构造划分:
经过运行上面的代码,我们就准备好了s[i][j],其中包含最佳分割信息。我们可以使用一种类似于中序遍历的方法来输出划分方式,比如对
void print_optimal_parens(int** s, int i, int j) {
if (i == j) {
cout << "A" << i;
} else {
cout << "(";
print_optimal_parens(s, i, s[i][j]);
print_optimal_parens(s, s[i][j] + 1, j);
cout << ")";
}
}比如对于数组p={5,6,2,9,7,6}和
最少乘法次数为:330次