主成分分析及R使用
目录
什么是主成分分析
主成分推导
主成分的分析过程
R语言计算
主成分分析注意事项
什么是主成分分析
principal-compon-analysis PCA,是将多指标化为少数几个综合指标的一种统计分析方法,由Pearson提出,由Hotelling发展,主成分分析是通过降维技术把多个变量化为少数几个主成分的方法,这些主成分保留原始变量的绝大部分信息,它们通常表示为原始变量的线性组合。
主成分推导
其中
求主成分就是求x的线性函数a'x,使相应的方差最大,即是
且a'a = 1,∑为x的协方差矩阵
主成分的分析过程
(1)将原始数据标准化,以消除变量间在数量级和量纲上的不同
(2)求标准化数据的相关矩阵
(3)求相关矩阵的特征值和特征向量
(4)计算方差贡献率与累积方差贡献率,每个主成分的贡献率代表了原数据总信息量的百分比。
(5)确定主成分:设C1,C2.....Cp为p个主成分,其中前m个主成分包含的数据信息总量不低于80%,可取前m个
主成分来反映原评价对象。
(6)用原指标的线性组合来计算各主成分得分:以各个主成分对原指标的相关系数(即载荷系数)为权,将各主成分表示为原指标的线性组合,而主成分的经济意义则由各线性组合中权数较大的指标的综合意义来确定,即
![]()
(7)综合得分:以个主成分的方差贡献率为权,将其线性组合得到综合评价函数。
(8)得分排序:利用总得分可以得到得分名次
R语言计算
在Excel中复制数据
x1:人均食品支出 x2:人均衣着商品支出 x3:人均家庭设备及服务支出 x4:未知 x5:人均交通和通信支出 x6:人均教育文化娱乐服务支出
x7:人均居住支出 x8:未知
X1 X2 X3 X4 X5 X6 X7 X8
北京 4934.05 1512.88 981.13 1294.07 2328.51 2383.96 1246.19 649.66
天津 4249.31 1024.15 760.56 1163.98 1309.94 1639.83 1417.45 463.64
河北 2789.85 975.94 546.75 833.51 1010.51 895.06 917.19 266.16
山西 2600.37 1064.61 477.74 640.22 1027.99 1054.05 991.77 245.07
内蒙古 2824.89 1396.86 561.71 719.13 1123.82 1245.09 941.79 468.17
辽宁 3560.21 1017.65 439.28 879.08 1033.36 1052.94 1047.04 400.16
吉林 2842.68 1127.09 407.35 854.8 873.88 997.75 1062.46 394.29
黑龙江 2633.18 1021.45 355.67 729.55 746.03 938.21 784.51 310.67
上海 6125.45 1330.05 959.49 857.11 3153.72 2653.67 1412.1 763.8
江苏 3928.71 990.03 707.31 689.37 1303.02 1699.26 1020.09 377.37
浙江 4892.58 1406.2 666.02 859.06 2473.4 2158.32 1168.08 467.52
安徽 3384.38 906.47 465.68 554.44 891.38 1169.99 850.24 309.3
福建 4296.22 940.72 645.4 502.41 1606.9 1426.34 1261.18 375.98
江西 3192.61 915.09 587.4 385.91 732.97 973.38 728.76 294.6
山东 3180.64 1238.34 661.03 708.58 1333.63 1191.18 1027.58 325.64
河南 2707.44 1053.13 549.14 626.55 858.33 936.55 795.39 300.19
湖北 3455.98 1046.62 550.16 525.32 903.02 1120.29 856.97 242.82
湖南 3243.88 1017.59 603.18 668.53 986.89 1285.24 869.59 315.82
广东 5056.68 814.57 853.18 752.52 2966.08 1994.86 1444.91 454.09
广西 3398.09 656.69 491.03 542.07 932.87 1050.04 803.04 277.43
海南 3546.67 452.85 519.99 503.78 1401.89 837.83 819.02 210.85
重庆 3674.28 1171.15 706.77 749.51 1118.79 1237.35 968.45 264.01
四川 3580.14 949.74 562.02 511.78 1074.91 1031.81 690.27 291.32
贵州 3122.46 910.3 463.56 354.52 895.04 1035.96 718.65 258.21
云南 3562.33 859.65 280.62 631.7 1034.71 705.51 673.07 174.23
西藏 3836.51 880.1 271.29 272.81 866.33 441.02 628.35 335.66
陕西 3063.69 910.29 513.08 678.38 866.76 1230.74 831.27 332.84
甘肃 2824.42 939.89 505.16 564.25 861.47 1058.66 768.28 353.65
青海 2803.45 898.54 484.71 613.24 785.27 953.87 641.93 331.38
宁夏 2760.74 994.47 480.84 645.98 859.04 863.36 910.68 302.17
新疆 2760.69 1183.69 475.23 598.78 890.3 896.79 736.99 331.8
计算相关矩阵
> X=read.table("clipboard",header=T) # 例7.2数据
> cor(X)
X1 X2 X3 X4 X5 X6 X7 X8
X1 1.0000000 0.2569697 0.7252526 0.3853672 0.8990457 0.8284572 0.7145260 0.7218909
X2 0.2569697 1.0000000 0.4537807 0.5765121 0.3575064 0.5420120 0.4045314 0.6277509
X3 0.7252526 0.4537807 1.0000000 0.5831419 0.7823418 0.8924742 0.7744004 0.7220538
X4 0.3853672 0.5765121 0.5831419 1.0000000 0.4665789 0.6291140 0.6911234 0.6254195
X5 0.8990457 0.3575064 0.7823418 0.4665789 1.0000000 0.8795439 0.7853531 0.7517683
X6 0.8284572 0.5420120 0.8924742 0.6291140 0.8795439 1.0000000 0.8133081 0.8435436
X7 0.7145260 0.4045314 0.7744004 0.6911234 0.7853531 0.8133081 1.0000000 0.7183218
X8 0.7218909 0.6277509 0.7220538 0.6254195 0.7517683 0.8435436 0.7183218 1.0000000
求相关矩阵的特征值和主成分负荷
> PCA=princomp(X,cor=T)#主成分分析
> PCA#特征值开根号结果
Call:
princomp(x = X, cor = T)
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
2.3877119 1.0142326 0.7101294 0.5222697 0.4314432 0.4015967 0.2955459 0.2415456
8 variables and 31 observations.> options(digits=3)#
> summary(PCA)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
Standard deviation 2.388 1.014 0.710 0.5223 0.4314 0.4016 0.2955 0.24155
Proportion of Variance 0.713 0.129 0.063 0.0341 0.0233 0.0202 0.0109 0.00729
Cumulative Proportion 0.713 0.841 0.904 0.9384 0.9616 0.9818 0.9927 1.00000
> > PCA$loadings#主成分载荷
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
X1 0.353 0.429 0.175 0.299 0.377 0.651
X2 0.249 -0.677 0.521 -0.399 0.129 0.134
X3 0.374 -0.789 0.261 0.116 0.372
X4 0.302 -0.472 -0.628 0.225 0.249 0.416
X5 0.376 0.324 0.123 0.127 -0.281 0.267 -0.695 0.298
X6 0.404 -0.200 0.132 -0.156 -0.857
X7 0.371 -0.442 -0.584 -0.535 0.166
X8 0.374 -0.118 0.282 0.409 0.522 -0.546 0.141
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
Proportion Var 0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125
Cumulative Var 0.125 0.250 0.375 0.500 0.625 0.750 0.875 1.000
> par(mar=c(4,4,2,1),cex=0.75)#
确定主成分
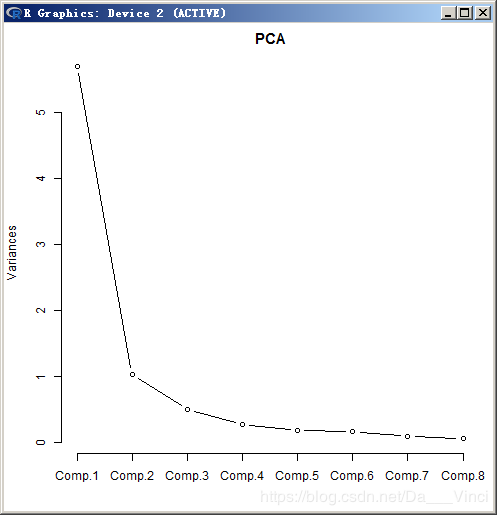
按照累积方差贡献路大于80%的原则,选定了两个主成分,其累积方差贡献率为80.7%,本例取m=2,从碎石图上看,m=2处拐点最大,所以合适
> screeplot(PCA,type="lines") #主成分得分
> PCA$scores #主成分得分
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
北京 6.1223 -1.523 -0.000699 -0.1666 0.8082 0.61705 0.03104 0.19770
天津 3.0101 -0.537 -1.983585 0.2402 0.2258 -0.29548 0.69032 0.00121
河北 -0.8875 -0.692 -1.007880 -0.1833 -0.0715 0.25073 -0.23041 0.33065
山西 -1.1037 -0.601 -0.372723 -0.2830 -0.8330 -0.18580 -0.33909 -0.20017
内蒙古 0.5333 -1.848 0.905240 0.0215 -0.1160 -0.58541 -0.27680 0.12987
辽宁 0.0944 -0.655 -0.732793 1.0840 0.0224 -0.12281 0.23872 0.03882
吉林 -0.3271 -1.425 -0.611769 0.8757 -0.2756 -0.50791 -0.06462 -0.05781
黑龙江 -1.6886 -0.996 -0.208530 0.5863 0.0814 0.07453 -0.29119 -0.25494
上海 7.0847 1.069 1.298471 0.4782 0.3712 -0.33451 -0.05759 0.04692
江苏 1.1413 0.454 -0.091151 -0.5652 0.2963 -0.05438 0.22236 -0.43523
浙江 3.8211 -0.172 0.891744 0.3821 -0.7426 0.82336 -0.22743 -0.43618
安徽 -1.1234 0.352 0.090623 0.1403 0.0870 -0.09203 0.14936 -0.40039
福建 1.1717 1.378 -0.003971 -0.0711 -0.7725 -0.75094 0.39610 -0.06020
江西 -1.6694 0.548 0.664092 -0.7411 0.3271 -0.31065 0.28215 0.08920
山东 0.4811 -0.808 0.101468 -0.6657 -0.6266 -0.04618 -0.07230 0.33552
河南 -1.2772 -0.648 0.090140 -0.4536 0.0795 -0.08396 -0.16619 0.20575
湖北 -1.0095 0.117 0.326878 -0.5400 -0.4086 0.22152 0.41805 -0.15476
湖南 -0.3651 -0.201 -0.052268 -0.4988 0.1991 0.07488 0.05201 -0.17998
广东 4.0320 2.480 -0.803479 -0.0976 -0.4886 -0.16234 -0.60865 0.21337
广西 -1.6274 1.231 -0.497570 0.0581 0.5171 -0.02017 0.00273 -0.21953
海南 -1.8731 2.353 -1.004127 -0.0164 0.3006 0.26584 -0.37735 0.29800
重庆 0.3940 -0.462 -0.170145 -0.9248 -0.3849 0.54185 0.52831 0.23121
四川 -1.1538 0.518 0.606682 -0.3346 0.3195 0.41484 0.14279 0.18693
贵州 -2.0140 0.659 0.763877 -0.3237 -0.0892 -0.08803 -0.04058 -0.28446
云南 -2.4295 0.418 -0.175907 0.9034 -0.3539 1.20455 0.07584 -0.01486
西藏 -2.7204 1.011 1.416453 1.2648 -0.0104 -0.13486 0.48220 0.45880
陕西 -0.8880 -0.117 -0.266061 -0.0258 0.4843 -0.06822 -0.11319 -0.36174
甘肃 -1.3245 -0.144 0.246081 -0.0897 0.4867 -0.36686 -0.26913 -0.08725
青海 -1.7685 -0.209 0.157700 -0.0141 0.8254 0.05345 -0.29206 0.02406
宁夏 -1.3173 -0.496 -0.306789 0.0148 -0.2028 -0.32443 -0.10741 0.14612
新疆 -1.3181 -1.053 0.729999 -0.0546 -0.0553 -0.00764 -0.17796 0.21333
>
结合前面的主成分载荷数据,对前两个主成分进行解释,C1与C2相比,C1在X3、X5、X6、X7、X8处较大,为家电,交通通讯、教育服务、居住等等支出,而C2在X1、X2、X4载荷较大,所以可视为食品衣物等消费。
各地区的主成分得分及排名如下
> library(mvstats) #
载入程辑包:‘mvstats’
The following object is masked _by_ ‘.GlobalEnv’:
H.clust
> princomp.rank(PCA,m=2)#主成分排名
Comp.1 Comp.2 PC rank
北京 6.1223 -1.523 4.9538 30
天津 3.0101 -0.537 2.4680 27
河北 -0.8875 -0.692 -0.8577 16
山西 -1.1037 -0.601 -1.0270 13
内蒙古 0.5333 -1.848 0.1694 22
辽宁 0.0944 -0.655 -0.0202 21
吉林 -0.3271 -1.425 -0.4948 19
黑龙江 -1.6886 -0.996 -1.5827 4
上海 7.0847 1.069 6.1652 31
江苏 1.1413 0.454 1.0362 25
浙江 3.8211 -0.172 3.2107 28
安徽 -1.1234 0.352 -0.8979 15
福建 1.1717 1.378 1.2032 26
江西 -1.6694 0.548 -1.3304 6
山东 0.4811 -0.808 0.2840 24
河南 -1.2772 -0.648 -1.1810 11
湖北 -1.0095 0.117 -0.8373 17
湖南 -0.3651 -0.201 -0.3399 20
广东 4.0320 2.480 3.7948 29
广西 -1.6274 1.231 -1.1905 10
海南 -1.8731 2.353 -1.2272 8
重庆 0.3940 -0.462 0.2631 23
四川 -1.1538 0.518 -0.8982 14
贵州 -2.0140 0.659 -1.6054 3
云南 -2.4295 0.418 -1.9943 2
西藏 -2.7204 1.011 -2.1501 1
陕西 -0.8880 -0.117 -0.7701 18
甘肃 -1.3245 -0.144 -1.1442 12
青海 -1.7685 -0.209 -1.5301 5
宁夏 -1.3173 -0.496 -1.1918 9
新疆 -1.3181 -1.053 -1.2776 7
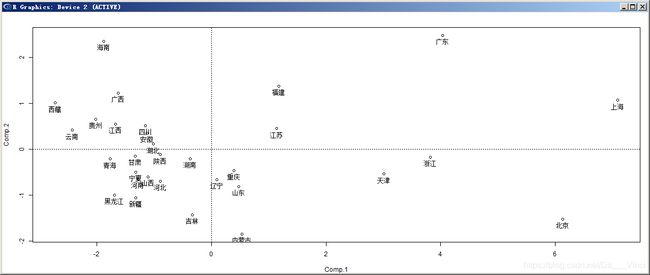
> > princomp.rank(PCA,m=2,plot=T)#主成分排名与作图
Comp.1 Comp.2 PC rank
北京 6.1223 -1.523 4.9538 30
天津 3.0101 -0.537 2.4680 27
河北 -0.8875 -0.692 -0.8577 16
山西 -1.1037 -0.601 -1.0270 13
内蒙古 0.5333 -1.848 0.1694 22
辽宁 0.0944 -0.655 -0.0202 21
吉林 -0.3271 -1.425 -0.4948 19
黑龙江 -1.6886 -0.996 -1.5827 4
上海 7.0847 1.069 6.1652 31
江苏 1.1413 0.454 1.0362 25
浙江 3.8211 -0.172 3.2107 28
安徽 -1.1234 0.352 -0.8979 15
福建 1.1717 1.378 1.2032 26
江西 -1.6694 0.548 -1.3304 6
山东 0.4811 -0.808 0.2840 24
河南 -1.2772 -0.648 -1.1810 11
湖北 -1.0095 0.117 -0.8373 17
湖南 -0.3651 -0.201 -0.3399 20
广东 4.0320 2.480 3.7948 29
广西 -1.6274 1.231 -1.1905 10
海南 -1.8731 2.353 -1.2272 8
重庆 0.3940 -0.462 0.2631 23
四川 -1.1538 0.518 -0.8982 14
贵州 -2.0140 0.659 -1.6054 3
云南 -2.4295 0.418 -1.9943 2
西藏 -2.7204 1.011 -2.1501 1
陕西 -0.8880 -0.117 -0.7701 18
甘肃 -1.3245 -0.144 -1.1442 12
青海 -1.7685 -0.209 -1.5301 5
宁夏 -1.3173 -0.496 -1.1918 9
新疆 -1.3181 -1.053 -1.2776 7
>
综合来看,北京、天津、上海、浙江、广东、等地的C1较高,而C1代表的多是第二产业、第三产业,与上述发达城市情形相符,西藏、新疆、广东、广西的C2值较高,C2代表的是食品服饰,西藏气候寒冷,广东广西因民族习惯在服饰上消费颇多。
主成分分析注意事项
主成分分析除了用来概述变量间关系外,也可以用来削减回归分析或聚类分析中变量数目,此外,为达到最大变异目的,我们可以用主成分分析将原来的变量转变为主成分,在抽出成分后,可将各变量的原始分数转换为成分分数,以供进一步深入的统计分析
。通常,在进行主成分分析时,应注意一下几点:
(1)主成分分析,可使用样本协方差阵或相关系数矩阵为出发点来进行分析,但大都以相关系数矩阵为主。
(2)为使方差达到最大,通常主成分分析是不加以主轴的。
(3)成分保留:主张将特征值小于1的成分予以放弃,而只保留大于1的成分。
(4)在实际研究里,研究者如果用不超过三个或五个成分就能解释变异的80%,就算令人满意。
(5)使用成分得分后,会使各变量的方差为最大,而且个变量之间会彼此独立正交。