回到原点
Let me think... 我们什么时候学过相关系数（Correlation）一个词语。对了，就是验证模型好坏的R方里面的R。在R语言里调用也很简单：
cor(x, y)但是，该如何理解相关系数呢？是否相关系数可以验证OLS模型的好坏呢？这是本篇博文所要探讨的事。
相关系数的定义
我们定义相关系数R为：
$$R = \frac{E(XY)-E(X)E(Y)}{\sqrt{[E(X^2) - E^2(X)][E(Y^2) - E^2(Y)]}}$$
我们看，这个相关系数到底代表着什么。
解释一：相关系数是两组数据距离中心点的度量
显然，我们可以转化以上的相关系数为：
$$R = \frac{\frac{(x - \bar{x})}{N}}{\sigma^2_x}·\frac{\frac{(y - \bar{y})}{N}}{\sigma^2_y}$$
这种方式理解的相关系数，其实是所有点与
$$(\bar{x}, \bar{y})$$
之间的距离标准化后的值。换句话说，R方式衡量到数据中心点的距离的一个标准。
解释二：去量纲的协方差
我们首先回到协方差(Covariance)的定义中来。协方差的定义为，
$$cov(x, y) = E[(x - \bar{x})(y - \bar{y})]$$
这个定义是从方差（Variance，试比较两者英文间的差距）的概念来的
$$var(x) = E[(x - \bar{x})(x - \bar{x})]$$
方差是描述一维数据的疏散程度，因此，协方差则是描述二维数据的疏散程度。这是理解协方差的一种手段。
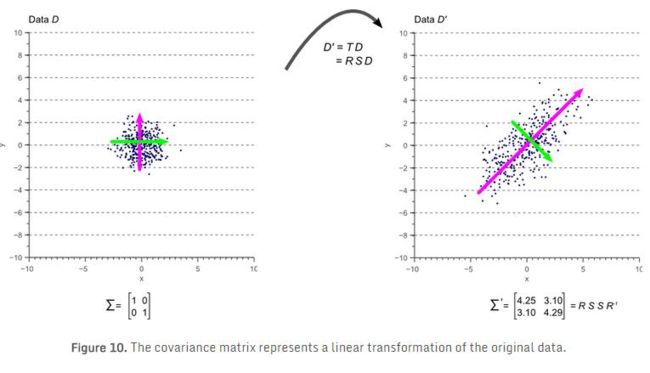
另一种手段是以白数据（数据只是在各个方向上符合高斯分布）的线性变换：
图片引用自会敲键盘的猩猩的博客
而后，显然，
$$R = \frac{cov(x, y)}{\sigma^2_x\sigma^2_y}$$
显然，这就是将协方差矩阵做了一次调整，使得对角线（不是反对角线）上的数据为1。这也就说明取消了协方差在自身变异上影响，此外，数值也被严格限定在了-1~1之间。
用同样地方法，我们也可以做出变异系数（coefficient of variation，cv）的概念：
$$cv(x) = \frac{\sigma}{\mu}$$
这个概念类似。是标准差去量纲的结果，通过这种处理，使得我们很容易两组数据的疏散程度，而不用考虑到本身数据的影响，因为cv本身是去量纲并严格限制在-1 ~ 1之间的度量。
提示：试通过协方差引申到PCA方法。
解释三：最小二乘法回归的模型误差来理解
这里直接使用的理解方式就是我们一般意义上的R方。
$$R^2 = 1 - \frac{\sum{(Y - \hat{Y})^2}}{\sum{(Y - \bar{Y})^2}}= 1 - \frac{SSE}{SSTO}$$
我们把上式中的SSTO称为总体方差，SSE称为模型误差。
因此我们看出
$$SSTO - SSE$$
是衡量模型好坏的方式：如果这个值很大，说明模型误差对总体方差的贡献较低；相反，贡献较高。而为了归一化这个值，最简单地方法就是除以SSTO使得度量值在0~1之间。
另一个准确地描述是，R方描述的是因变量的方差有多少比例通过自变量模型所解释。
这就是相关系数的平方为什么能衡量模型好坏的原因。
相关系数的局限
高的R方不一定代表模型的预测能力强。R方无法考虑过拟合。
R方并不能保证拟合效果。原因是我们可以看出，R方基于的假设其实是一个二维的高斯分布，或者说，R方只能预测某种线性趋势。如果遇到明显的非线性关系，显然R方是无效的。
其实相关系数不止一种
我们称之前描述的相关系数为Pearson相关系数。我们看到了Pearson相关系数的种种局限，因此，为了避免相关系数无法解释非线性关系这个问题，其他种的相关系数也被发明出来。在此介绍两种常见的替代方案：Kendall Tau相关系数和Spearman相关系数。这两种系数的特点是，其实都是基于顺序的相关系数。
Kendall Tau相关系数
Kendall Tau相关系数的原理相当简单，假设就是：
i) 如果x和y有同增的关系，则对于任何$$(x_i, y_i), (x_j, y_i)$$，如果$$x_i < x_j$$，则$$y_i < y_j$$
ii) 相反，如果x和y有同减的关系，则如果$$x_i < x_j$$，则$$y_i > y_j$$
因此我们可以检查所有点对（Point Pairs，即两个二维点），计算二维数据里面符合条件i)的点对（一致点对，concordant point pairs）对数目和ii)的点对(不一致点对，discordant point pairs)数目，如果这两个值的差值来描述关系。显然如果两种情况的点数目大致相当，说明两个维度关系相当“混乱”。
此外，我们要讲这个值归一化，简单地，除以点对的总数目即可，显然点对个数为，
$${n \choose 2} = \frac{(n-1)n}{2}$$
因此，最后计算的kendall tau相关系数为：
$$\tau = \frac{\#concordant - \#discordant}{n(n - 1)/2}$$
当然，我们基于这个假设，可以很容易看出，
kendall tau相关系数的使用场景比较多，因为kendall tau不依赖于线性假说。
kendall tau相关系数描述的两组数的单调性特征，任何一种单调的关系都可以采用kendall tau来实现。
Spearman相关系数
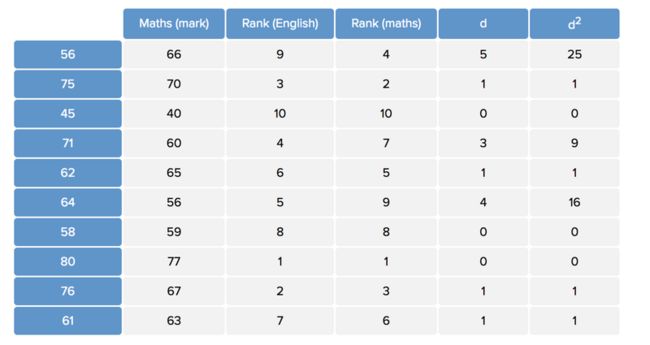
Spearman相关系数与Pearson相关系数很类似，只是最后计算的是两个变量转化为序数（Rank）的操作。可以参考下面的转换：
我们用rg(x)表示x的序数变换，d为序数之差，因此：
$$cor_{spearman}(x, y) = \frac{cov(rg(x), rg(y))}{\sigma^2_{rg(x)}\sigma^2_{rg(y)}} = 1 - \frac{6d_i^2}{n(n^2 - 1)}$$
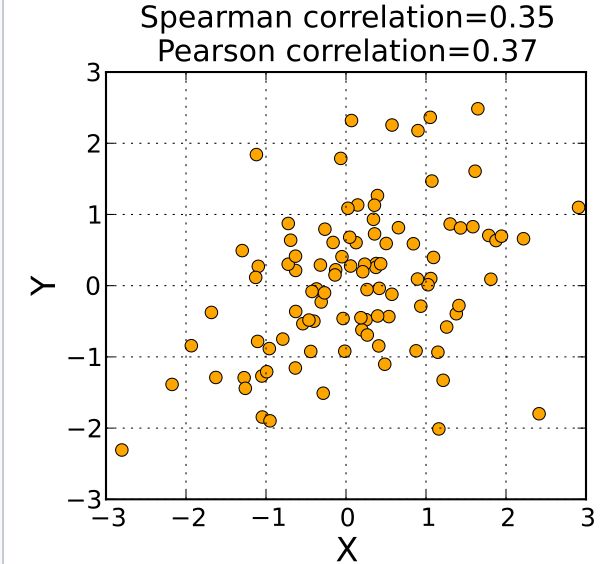
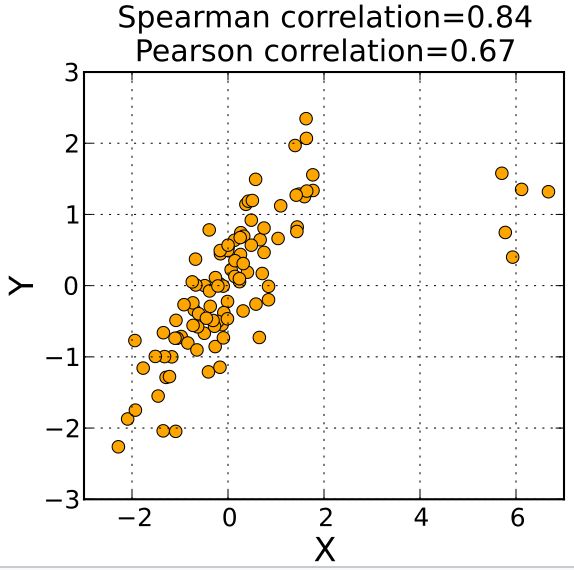
Spearman相关系数的优点是显然的：
当数据具有非线性相关时，Spearman相关系数敏感度比Pearson要好
当没有outliers时，Spearman和Pearson结果类似
当有outliers时，Spearman比较稳健
相关系数、相似度、距离
我们在此讨论相关系数的其他应用。
特征工程的相关系数
相关系数描述的是因变量与自变量的关系这个直接可以作为筛选特征的一个标准。
自变量与自变量的Pearson相关系数很强也往往意味着共线性，这提示PCA降维的效果会非常好。
相关系数 = 相似度
我们回到相关系数的性质，相关系数描述的是两个自变量之间的关系是否紧密，其实一定程度就是描述相似性，即两个向量的相似性。
这提示，相关系数可以作为相似度（Similarity）用来建构协同过滤的推荐系统。这种方案也被叫做Pearson相似度。我们可以以此来比较Pearson相似度和余弦相似度是类似模式，Pearson相似度是去中心化的余弦相似度：
$$Sim_{cosine} = \frac{\lt x, y\gt}{||x||·||y||}$$
$$Sim_{pearson} = \frac{\lt (x - \bar{x}), (y - \bar{y})\gt}{||(x - \bar{x})||·||y - \bar{y})||}$$
相似度即距离的反面
首先，我们要有一个敏感度，任何相似度都可以作为距离的度量。而事实上，我们经常用（1 - 归一化后的相似度）来表示距离。
而，距离对我们来说意味着什么？距离意味着所有依赖距离的方法都可以运用到相关系数。
KMeans聚类
KMeans聚类是一个常见地基于距离假设的模型。可以构想的例子是，在做用户分类的时候，可以把他们购买某一些商品（往往具有一类特征的商品）的矩阵转化为一个相关系数的特征，从而获得具有解释性的模型。
社交网络分析
网络分析是另一个典型的基于距离的门类，因此，基于所有用户之间的距离（值得注意的是，相关系数形成的网络很有可能是个全连接的网络）可以完成所有网络分析技术（节点的中心特征，社群特征等）。