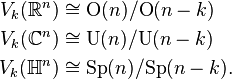Stiefel manifold
In mathematics , the Stiefel manifold V k (R n ) is the set of all orthonormal k -frames in R n . That is, it is the set of ordered k -tuples of orthonormal vectors in R n . It is named after Swiss mathematician Eduard Stiefel . Likewise one can define the complex Stiefel manifold V k (C n ) of orthonormal k -frames in C n and the quaternionic Stiefel manifold V k (H n ) of orthonormal k -frames in H n . More generally, the construction applies to any real, complex, or quaternionic inner product space .
In some contexts, a non-compact Stiefel manifold is defined as the set of all linearly independent k -frames in R n , C n , or H n ; this is homotopy equivalent, as the compact Stiefel manifold is a deformation retract of the non-compact one, by Gram–Schmidt . Statements about the non-compact form correspond to those for the compact form, replacing the orthogonal group (or unitary or symplectic group) with the general linear group .
Contents[hide ]
|
[edit ] Topology
Let F stand for R , C , or H . The Stiefel manifold V k (F n ) can be thought of as a set of n × k matrices by writing a k -frame as a matrix of k column vectors in F n . The orthonormality condition is expressed by A *A = 1 where A * denotes the conjugate transpose of A and 1 denotes the k × k identity matrix . We then have
The topology on V k (F n ) is the subspace topology inherited from F n ×k . With this topology V k (F n ) is a compact manifold whose dimension is given by
[edit ] As a homogeneous space
Each of the Stiefel manifolds V k (F n ) can be viewed as a homogeneous space for the action of a classical group in a natural manner.
Every orthogonal transformation of a k -frame in R n results in another k -frame, and any two k -frames are related by some orthogonal transformation. In other words, the orthogonal group O(n ) acts transitively on V k (R n ). The stabilizer subgroup of a given frame is the subgroup isomorphic to O(n −k ) which acts nontrivially on the orthogonal complement of the space spanned by that frame.
Likewise the unitary group U(n ) acts transitively on V k (C n ) with stabilizer subgroup U(n −k ) and the symplectic group Sp(n ) acts transitively on V k (H n ) with stabilizer subgroup Sp(n −k ).
In each case V k (F n ) can be viewed as a homogeneous space:
When k = n , the corresponding action is free so that the Stiefel manifold V n (F n ) is a principal homogeneous space for the corresponding classical group.
When k is strictly less than n then the special orthogonal group SO(n ) also acts transitively on V k (R n ) with stabilizer subgroup isomorphic to SO(n −k ) so that
The same holds for the action of the special unitary group on V k (C n )
Thus for k = n − 1, the Stiefel manifold is a principal homogeneous space for the corresponding special classical group.
[edit ] Special cases
| k = 1 |  |
| k = n −1 |  |
| k = n |  |
A 1-frame in F n is nothing but a unit vector, so the Stiefel manifold V 1 (F n ) is just the unit sphere in F n .
Given a 2-frame in R n , let the first vector define a point in S n −1 and the second a unit tangent vector to the sphere at that point. In this way, the Stiefel manifold V 2 (R n ) may be identified with the unit tangent bundle to S n −1 .
When k = n or n −1 we saw in the previous section that V k (F n ) is a principal homogeneous space, and therefore diffeomorphic to the corresponding classical group. These are listed in the table at the right.
[edit ] As a principal bundle
There is a natural projection
from the Stiefel manifold V k (F n ) to the Grassmannian of k -planes in F n which sends a k -frame to the subspace spanned by that frame. The fiber over a given point P in G k (F n ) is the set of all orthonormal k -frames contained in the space P .
This projection has the structure of a principal G -bundle where G is the associated classical group of degree k . Take the real case for concreteness. There is a natural right action of O(k ) on V k (R n ) which rotates a k -frame in the space it spans. This action is free but not transitive. The orbits of this action are precisely the orthonormal k -frames spanning a given k -dimensional subspace; that is, they are the fibers of the map p . Similar arguments hold in the complex and quaternionic cases.
We then have a sequence of principal bundles:
The vector bundles associated to these principal bundles via the natural action of G on F k are just the tautological bundles over the Grassmannians. In other words, the Stiefel manifold V k (F n ) is the orthogonal, unitary, or symplectic frame bundle associated to the tautological bundle on a Grassmannian.
When one passes to the n → ∞ limit, these bundles become the universal bundles for the classical groups.
[edit ] Homotopy
The Stiefel manifolds fit into a family of fibrations 
, thus the first non-trivial homotopy group of the space 
is in dimension n − k . Moreover, 
if 
or if k = 1 . 
if n − k is odd and k > 1 . This result is used in the obstruction-theoretic definition of Stiefel-Whitney classes .
[edit ] See also
- Flag manifold
[edit ] References
- Hatcher, Allen (2002). Algebraic Topology . Cambridge University Press. ISBN 0-521-79540-0 .
- Husemoller, Dale (1994). Fibre Bundles ((3rd ed.) ed.). New York: Springer-Verlag. ISBN 0-387-94087-1 .
- James, Ioan Mackenzie (1976). The topology of Stiefel manifolds . CUP Archive. ISBN 978-0-52121334-9 .
[edit ] External links
- Encyclopaedia of Mathematics » Stiefel manifold , Springer