《Schwarz-Christoffel Mapping》笔记
Schwarz-Christoffel Mapping
本笔记不全,跳过了部分内容,并持续更新~
Chapter 1: Introduction
1.1 The Schwarz-Christoffel Idea
Schwarz-Christoffel变换背后的想法是,任何共形映射(conformal mapping) f f f都有导数: f ′ = ∏ f k f'=\prod f_k f′=∏fk,其中 f k f_k fk是一系列典型(canonical)函数。这个公式的重要性在于辐角 arg f ′ = ∑ arg f k \arg f'=\sum\arg f_k argf′=∑argfk。在classical变换中,所有 arg f k \arg f_k argfk都设计为一个阶跃函数,所以 arg f ′ \arg f' argf′是一个带有特定阶跃的分段常数(如 f f f将实轴映射到多边形上)。设 P P P为多边形 Γ \Gamma Γ包围的复平面,顶点为 w 1 , ⋯ , w n w_1,\cdots,w_n w1,⋯,wn,内角为 α 1 π , ⋯ , α n π \alpha_1\pi, \cdots, \alpha_n\pi α1π,⋯,αnπ,其中 α k ∈ ( 0 , 2 ) \alpha_k\in(0,2) αk∈(0,2)。设共形映射 f f f将上半平面 H + H^+ H+映射到 P P P上,并设 z k = f − 1 ( w k ) z_k=f^{-1}(w_k) zk=f−1(wk)是第 k k k个prevertex。我们可以不失一般性地假设 z n = ∞ z_n=\infin zn=∞,即实轴上的无穷映射到多边形最后一个顶点上,因为即使 ∞ \infin ∞还不是prevertex,我们也可以将其image设为一个新的内角为 π \pi π的顶点。其余的prevertices z 1 , ⋯ , z n − 1 z_1,\cdots,z_{n-1} z1,⋯,zn−1都是真的。
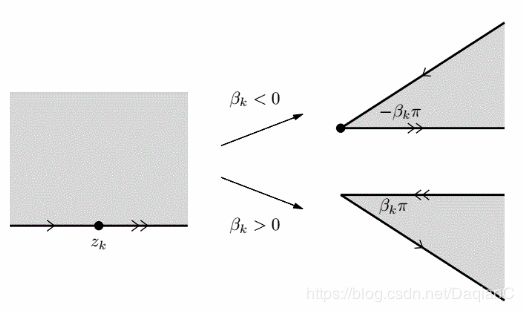
在线段 ( z k , z k + 1 ) (z_k,z_{k+1}) (zk,zk+1)之间, f f f是分析连续的,即 f ′ f' f′存在,且 arg f ′ \arg f' argf′是常数并在 z k z_k zk处有阶跃,即 [ arg f ′ ( z ) ] z k − z k + = ( 1 − α k ) π = β k π [\arg f'(z)]_{z_k^-}^{z_k^+}=(1-\alpha_k)\pi=\beta_k\pi [argf′(z)]zk−zk+=(1−αk)π=βkπ,其中 β k π \beta_k\pi βkπ是在第k个顶点处的转角。我们可以根据以上条件设定函数 f k = ( z − z k ) − β k f_k=(z-z_k)^{-\beta_k} fk=(z−zk)−βk。下图示意了实轴经过 f k f_k fk映射的结果。
定理1.1: 设P是多边形 Γ \Gamma Γ的内部,顶点为 w 1 , ⋯ , w n w_1,\cdots,w_n w1,⋯,wn(逆时针),内角为 α 1 π , ⋯ , α n π \alpha_1\pi, \cdots, \alpha_n\pi α1π,⋯,αnπ,定义 f f f是将上半平面 H + H_+ H+变换到 P P P的任意共形映射,且 f ( ∞ ) = w n f(\infin)=w_n f(∞)=wn,则 f ( z ) = A + C ∫ z ∏ k = 1 n − 1 ( ζ − z k ) a k − 1 d ζ f(z)=A+C\int^z\prod_{k=1}^{n-1}(\zeta-z_k)^{a_k-1} d \zeta f(z)=A+C∫zk=1∏n−1(ζ−zk)ak−1dζ其中 A , C A,C A,C都是复常数,且对于 k = 1 , ⋯ , n − 1 k=1, \cdots ,n-1 k=1,⋯,n−1都有 w k = f ( z k ) w_k=f(z_k) wk=f(zk)。
以上公式可以用于映射不同的区域(如单位圆)、有branch points的区域、多连通区域、边界为圆弧的区域、甚至是边界分段解析的区域,在第四章中说明。
问题来了:我们不知道prevertices z k z_k zk是多少,那也就没法用定理1.1计算映射。从定理中可以发现,无论 z k z_k zk是多少,多边形的内角都是不变的,这由 a k a_k ak决定。也就是说,如果 z k z_k zk选的不好,映射出来的多边形只是内角与目标多边形相同,而边长不同。 z k z_k zk的确定称为Schwarz-Christoffel parameter problem,并且需要在使用SC方程之前求解。具体求解方法在第二章中讲述。
在应用中, z k z_k zk非线性地取决于多边形的边长,没有解析解,因此经常使用数值计算来计算定理1.1中的积分。数值问题在第三章中讨论。
1.2 历史
共形映射起源于19世纪。黎曼在1851年提出了黎曼映射定理,说复平面上任何单连通区域,只要不是整个复平面,就可以互相进行共形映射。Schwarz-Christoffel公式随后提出。
Christoffel在1867年于ETH Zurich发表了第一篇关于SC公式的论文,发现了在多边形域内,格林方程可以通过对半平面进行共形映射获得。随后他扩展到多边形外部与曲线区域。
Schwarz与1869年独立提出相同的理论,但侧重于数值和特定情境,如三角形;他甚至发表了首个SC映射的plot。论文中还包含了他的著名的反射原理:如果一个解析函数 f f f被连续扩展到一个直线或圆弧边界,并将边界弧映射到另一个直线或者圆弧上,则 f f f可以被解析地continued across the arc by reflection。
在SC公式发现的130年后,它在理论复分析中产生了巨大影响,用于证明黎曼映射定理与其推论。在计算机发明以后,SC公式用于具体应用。
在20世纪下半夜,有很多关于算法和程序的工作,但质量不高、综合性不强;很多重要问题都被忽视,如SC积分的快速计算,还有在解参数问题时prevertices的顺序。最综合的程序应当是Trefethen在1980年写的SCPACK和Driscoll在1996年发布的SC Toolbox。
Chapter 2: Essentials of Schwarz-Christoffel mapping
2.1 多边形
定义多边形 Γ \Gamma Γ,顶点为 w 1 , ⋯ , w n w_1,\cdots,w_n w1,⋯,wn(逆时针),内角为 α 1 π , ⋯ , α n π \alpha_1\pi, \cdots, \alpha_n\pi α1π,⋯,αnπ,并扩展定义 w n + 1 = w 1 w_{n+1}=w_1 wn+1=w1与 w 0 = w n w_0=w_n w0=wn。
内角 α k \alpha_k αk的定义是从 w k w_k wk的incoming边到outgoing边的扫过的角度。如果 ∣ w k ∣ < ∞ |w_k|<\infin ∣wk∣<∞,则 α k ∈ ( 0 , 2 ] \alpha_k\in(0,2] αk∈(0,2]。如果 α k = 2 \alpha_k=2 αk=2,则两边重合, w k w_k wk是这个裂缝(slit)的尖尖。如果 w k = ∞ w_k=\infin wk=∞,则 α k ∈ [ − 2 , 0 ] \alpha_k\in[-2,0] αk∈[−2,0]。如果 w k w_k wk与其相邻顶点都是有限的,则指定 α k \alpha_k αk是冗余的,但如果不是,则就需要确定 α k \alpha_k αk来保证多边形唯一。
同时要求外角和为 2 π 2\pi 2π,即 ∑ k = 1 n α k = n − 2 \sum_{k=1}^n\alpha_k=n-2 ∑k=1nαk=n−2。还要求是简单多边形,即不能自己穿过自己(多次覆盖某一个区域)。
2.2 The Schwarz-Christoffel formula
定理2.1(即定理1.1):半平面的SC方程
设P是多边形 Γ \Gamma Γ的内部,顶点为 w 1 , ⋯ , w n w_1,\cdots,w_n w1,⋯,wn(逆时针),内角为 α 1 π , ⋯ , α n π \alpha_1\pi, \cdots, \alpha_n\pi α1π,⋯,αnπ,定义 f f f是将上半平面 H + H_+ H+变换到 P P P的任意共形映射,且 f ( ∞ ) = w n f(\infin)=w_n f(∞)=wn,则 f ( z ) = A + C ∫ z ∏ k = 1 n − 1 ( ζ − z k ) a k − 1 d ζ f(z)=A+C\int^z\prod_{k=1}^{n-1}(\zeta-z_k)^{a_k-1} d \zeta f(z)=A+C∫zk=1∏n−1(ζ−zk)ak−1dζ其中 A , C A,C A,C都是复常数,且对于 k = 1 , ⋯ , n − 1 k=1, \cdots ,n-1 k=1,⋯,n−1都有 w k = f ( z k ) w_k=f(z_k) wk=f(zk)。
证明略过…
定理2.2:圆的SC方程
设P是多边形 Γ \Gamma Γ的内部,顶点为 w 1 , ⋯ , w n w_1,\cdots,w_n w1,⋯,wn(逆时针),内角为 α 1 π , ⋯ , α n π \alpha_1\pi, \cdots, \alpha_n\pi α1π,⋯,αnπ。定义 f f f是从单位圆 E E E到 P P P的共形映射,则 f ( z ) = A + C ∫ z ∏ k = 1 n ( 1 − ζ z k ) a k − 1 d ζ f(z)=A+C\int^z\prod_{k=1}^{n}\left(1-\frac{\zeta}{z_k}\right)^{a_k-1}d\zeta f(z)=A+C∫zk=1∏n(1−zkζ)ak−1dζ其中 A , C A,C A,C都是复常数,且对于 k = 1 , ⋯ , n − 1 k=1, \cdots ,n-1 k=1,⋯,n−1都有 w k = f ( z k ) w_k=f(z_k) wk=f(zk)。
以上定理可由SC原理导出,参考章节4.1。两个定理的区别在于,后者是 n n n项乘积,前者是 n − 1 n-1 n−1项。两个积分项看起来不同,但实际上只是差常数倍。
2.3 单顶点或双顶点的多边形
SC方程仅是准明确的(quasi-explicit):必须首先确定prevertices z k z_k zk与常数A和C,才能计算映射。选择上有一定灵活性:基于黎曼映射定理,可以在 R ∪ { ∞ } \mathbf{R}\cup\{\infin\} R∪{∞}上随便选三个点,作为多边形 Γ \Gamma Γ上的随意三个点的映射,只要顺序是一样的。换句话说,映射中有三个自由度,这让我们可以随意选取三个prevertices。因此,如果 n ≤ 3 n\leq3 n≤3,则没有需要求解的参数。
n = 1 n=1 n=1时,多边形是直线, w 1 = ∞ , α 1 = − 1 w_1=\infin,\alpha_1=-1 w1=∞,α1=−1。因此半平面公式为 f ( z ) = A + C z f(z)=A+Cz f(z)=A+Cz,可进行尺度变换、旋转、平移;单位圆公式为 f ( z ) = A + C z − z 1 f(z)=A+\frac{C}{z-z_1} f(z)=A+z−z1C,仍然有两个自由度,可以通过设定0的映射图像(或称共形中心)来确定。
n = 2 n=2 n=2时,有 α 1 + α 2 = 0 \alpha_1+\alpha_2=0 α1+α2=0,所以要么两个都是0,要么相反数。对于前者,两个顶点都是无穷,因此区域 P P P是一个条带(strip)。此时半平面映射为 f ( z ) = A + C log ( z − z 1 ) f(z)=A+C\log(z-z_1) f(z)=A+Clog(z−z1),单位圆映射为 f ( z ) = A + C log ( z − z 1 z − z 2 ) f(z)=A+C\log\left(\frac{z-z_1}{z-z_2}\right) f(z)=A+Clog(z−z2z−z1)。如果只取上半个单位圆,因为对称,则发现它映射到原条带的上半个宽度;如果再将上半个圆内部区域以圆这条曲线向外反射,则得到整个上半平面,即可以得到另一个上半平面到条带的映射。区域分割和反射是扩展SC映射应用的常用手段。
对于后者,即 α 1 = − α 2 ≠ 0 \alpha_1=-\alpha_2\neq 0 α1=−α2̸=0,可知一个顶点是有限的,另一个无限(设 w 2 w_2 w2无限)。则区域P是一个楔形,顶角为 w 1 w_1 w1,半平面公式为 f ( z ) = A + C ( z − z 1 ) α 1 f(z)=A+C(z-z_1)^{\alpha_1} f(z)=A+C(z−z1)α1。对于 α 1 < 1 \alpha_1<1 α1<1(既<180°),网格线远离顶角,称salient或convex角;对于 α 1 > 1 \alpha_1>1 α1>1,网格线聚集于顶角,成为reentrant(折返)或concave(凹)角。这里有很多物理应用,如后者可以表示压力分布,这就是为什么飞机窗户没有尖角。
2.4 三角形
有三个顶点的多边形是可以随意选prevertices的情况中( n ≤ 3 n\leq 3 n≤3)最常用的一个。本章节中三角形既指代无界多边形,也指代普通三角形,但前者更有意思。
因为 α 1 + α 2 + α 3 = 1 \alpha_1+\alpha_2+\alpha_3=1 α1+α2+α3=1,因此最多顶点两个无限(设为 w 1 w_1 w1和 w 3 w_3 w3),此时 α 2 ≥ 1 \alpha_2\geq 1 α2≥1(如果 ≤ 1 \leq 1 ≤1的话,就是没有无限顶点的普通三角形了),既 w 2 w_2 w2角是折返角,因此区域P是一个一边凹进去的条带。映射的方法是先将普通条带下的直角坐标网格移植到圆下,然后再到有凹陷的条带下。当 α 2 = 2 \alpha_2=2 α2=2时,凹陷对折成一个裂缝。
对于只有一个无限顶点的三角形,有很多应用价值,不同形态有不同closed form的映射函数,略过。
对于到任意三角形的SC映射,可以用不完全beta函数: B z ( p , q ) = ∫ 0 z ζ p − 1 ( 1 − ζ ) q − 1 d ζ B_z(p,q)=\int_0^z\zeta^{p-1}(1-\zeta)^{q-1}d\zeta Bz(p,q)=∫0zζp−1(1−ζ)q−1dζ。
2.5 矩形与椭圆函数
如果 n = 4 n=4 n=4,则不能随意选prevertices,且没有解析解;但因为矩形有对称性,对于矩形有explicit解。
设矩形在复平面上的四个顶点是 w 1 = − K + i K ′ , w 2 = − K , w 3 = K , w 4 = K + i K ′ w_1=-K+i K', w_2=-K, w_3 = K, w_4=K+iK' w1=−K+iK′,w2=−K,w3=K,w4=K+iK′;因为对称性,我们选择prevertices为 z 1 = − m − 1 / 2 , z 2 = − 1 , z 3 = 1 , z 4 = m − 1 / 2 z_1=-m^{-1/2}, z_2=-1, z_3=1, z_4=m^{-1/2} z1=−m−1/2,z2=−1,z3=1,z4=m−1/2,其中 m m m是代表自由度的参数。0的映射是0,无穷的映射是点 i K ′ iK' iK′。此时映射函数为 f ( z ) = A + C ∫ z ∏ k = 1 4 ( ζ − z k ) − 1 / 2 d ζ = C ∫ 0 s i n − 1 z d θ 1 − m sin 2 θ f(z)=A+C\int^z\prod_{k=1}^4(\zeta-z_k)^{-1/2}d\zeta=C\int_0^{sin^{-1}z}\frac{d\theta}{\sqrt{1-m\sin^2\theta}} f(z)=A+C∫z∏k=14(ζ−zk)−1/2dζ=C∫0sin−1z1−msin2θdθ,即 sn ( C − 1 w ∣ m ) = z \text{sn}(C^{-1}w|m)=z sn(C−1w∣m)=z,其中 sn ( u ∣ m ) \text{sn}(u|m) sn(u∣m)是Jacobi elliptic sine,如果矩形进行了尺度归一化,即 K = f ( 1 ) K=f(1) K=f(1),可得 C = 1 C=1 C=1,进而可以直接得到逆映射 z = sn ( w ∣ m ) z=\text{sn}(w|m) z=sn(w∣m)。
椭圆参数 m m m与矩形的aspect ratio一一对应,因此SC参数问题本质上是求 m m m,使 K ′ ( m ) / 2 K ( m ) K'(m)/2K(m) K′(m)/2K(m)等于aspect ratio。
这个矩形的变换与广义四边形(generalized quadrilateral)紧密相关。广义四边形Q是一个Jordan区域(即单位圆经映射后得到的区域)加上边界上四个点a、b、c、d。一个将区域Q映射到上半平面 H + H^+ H+的共形映射将点a、b、c、d映射到实轴上的几个点,即可以通过Mobius变换映射到点 ± 1 \pm1 ±1与 ± m − 1 / 2 \pm m^{-1/2} ±m−1/2。因此:一个广义四边形可以经过两次映射(先到上半平面,再经过SC变换)得到一个矩形,但是第一次映射中映射到上半平面之后的四个顶点是确定的,因此只能得到某个特定的aspect ratio的矩形。这个aspect ratio称作广义四边形Q的conformal modulus,其取决于区域的四个边界点选择,还有区域的形状。如果两个区域的modulus相同,则他们conformally相等。
2.6 Crowding
Crowding是一种病态,会给几乎所有共形映射的数值方法带来问题。可以用单位圆到矩形的映射来说明:当aspect ratio越来越大时,某些曲线之间的夹角指数减小, m = O ( e − 2 π a ) m=O(e^{-2\pi a}) m=O(e−2πa),即在disk map中的两个prevertices相距 O ( e − π a / 2 ) O(e^{-\pi a/2}) O(e−πa/2),即越来越近,因此两prevertices之间的导数越来越大,即对disk中一个点进行轻微变化(如果四舍五入),得到的映射都会产生很大变化。
Crowding不仅影响矩形映射,而是影响任何狭长(elongated)的形状。一种常用的解决手段是使用domain decomposition(域分解)。
Chapter 3: Numerical Methods
在写作这本书的时候(2002年),对十几、二十几个prevertices计算到8位精确数字只需要几秒钟时间,几百个prevertices可以在几分钟内计算出来(现在计算机应该已经快了一千倍,也就是几ms?)。
在本章节中将讨论SC映射的主要算法问题,并讲解从单位圆的映射 (经常是计算最方便的)。
3.1 边长参数问题
回忆单位圆的SC公式: f ( z ) = A + C ∫ z ∏ k = 1 n ( 1 − ζ z k ) α k − 1 d ζ f(z)=A+C\int^z\prod_{k=1}^{n}\left(1-\frac{\zeta}{z_k}\right)^{\alpha_k-1}d\zeta f(z)=A+C∫z∏k=1n(1−zkζ)αk−1dζ。第一章中讲,积分中的指数部分决定了映射的角度,与prevertices的位置无关,而后者决定了映射图像的边长。因此必须通过设定条件来求解它。
我们首先可以确定映射中的三个自由度,即设定 z n − 2 = − 1 , z n − 1 = − i , z n = 1 z_{n-2}=-1,z_{n-1}=-i,z_n=1 zn−2=−1,zn−1=−i,zn=1,并剩下 n − 3 n-3 n−3个量要确定。对于一个有界多边形,这即可通过 n − 3 n-3 n−3个实条件来达成: ∣ ∫ z j z j + 1 f ′ ( ζ ) d ζ ∣ ∣ ∫ z 1 z 2 f ′ ( ζ ) d ζ ∣ = ∣ w j + 1 − w j ∣ ∣ w 2 − w 1 ∣ , j = 2 , 3 , ⋯ , n − 2 \frac{\left|\int_{z_j}^{z_{j+1}}f'(\zeta)d\zeta\right|}{\left|\int_{z_1}^{z_2}f'(\zeta)d\zeta\right|}=\frac{\left|w_{j+1}-w_j\right|}{\left|w_2-w_1\right|}, \ \ j=2,3,\cdots,n-2 ∣∣∣∫z1z2f′(ζ)dζ∣∣∣∣∣∣∫zjzj+1f′(ζ)dζ∣∣∣=∣w2−w1∣∣wj+1−wj∣, j=2,3,⋯,n−2。
定理3.1: 假设 α n ≠ 1 \alpha_n\neq1 αn̸=1且 α n ≠ 2 \alpha_n\neq2 αn̸=2(即 w n w_n wn左右两边不共线),则一个有界多边形被其内角和上述公式右侧列写的 n − 3 n-3 n−3个边长唯一确定,不包括尺度、旋转、平移。
证明:因为可以进行尺度、旋转、平移变换,我们可以假设 w 1 w_1 w1和 w 2 w_2 w2都是正确的。因为知道 ∣ w 3 − w 2 ∣ |w_3-w_2| ∣w3−w2∣边长和 w 2 w_2 w2处的内角,所以 w 3 w_3 w3也知道,同理可推到 w n − 1 w_{n-1} wn−1。因为 α n \alpha_n αn不是180度,也不是360度,所以 w n w_n wn的两条边不平行,所以可以基于 α 1 \alpha_1 α1和 α n − 1 \alpha_{n-1} αn−1推出 w n w_n wn。
尺度、旋转和平移由常数A和C决定,但是方便的是这两个常数不出现在上述条件中。
如果 w J = ∞ , J < n w_J=\infin, J<n wJ=∞,J<n,则有两个条件无意义,可以替换成另一个复条件: ∫ z J − 1 z J + 1 f ′ ( ζ ) d ζ ∣ ∫ z 1 z 2 f ′ ( ζ ) d ζ ∣ = w J + 1 − w J − 1 ∣ w 2 − w 1 ∣ \frac{\int_{z_{J-1}}^{z_{J+1}}f'(\zeta)d\zeta}{\left|\int_{z_1}^{z_2}f'(\zeta)d\zeta\right|}=\frac{w_{J+1}-w_{J-1}}{\left|w_2-w_1\right|} ∣∣∫z1z2f′(ζ)dζ∣∣∫zJ−1zJ+1f′(ζ)dζ=∣w2−w1∣wJ+1−wJ−1,这个条件保证 w j w_j wj两侧的两边的相对位置。我们必须要求不能有两个相邻的无穷顶点,如果有,可以在两点之间引入另一个顶点,内角为 π \pi π。
我们现在有了 n − 3 n-3 n−3个关于未知prevertices的条件,当求解时,需要保证他们在单位圆上按顺序排列。定义 z k z_k zk的辐角为 θ k \theta_k θk,则 0 < θ 1 < θ 2 < ⋯ < θ n = 2 π 0<\theta_1<\theta_2<\cdots <\theta_n=2\pi 0<θ1<θ2<⋯<θn=2π。我们已经设定了 θ n − 2 = π \theta_{n-2}=\pi θn−2=π和 θ n − 1 = 3 π 2 \theta_{n-1}=\frac{3\pi}{2} θn−1=23π。因为有约束的方程比较难解,我们转化成等价的无约束的方程: ϕ k = log ( θ k − θ k − 1 θ k + 1 − θ k ) , k = 1 , ⋯ , n − 3 \phi_k=\log\left(\frac{\theta_k-\theta_{k-1}}{\theta_{k+1}-\theta_k}\right), \ k=1,\cdots,n-3 ϕk=log(θk+1−θkθk−θk−1), k=1,⋯,n−3。其中如前文提到, θ 0 = 0 \theta_0=0 θ0=0。由此可以得到prevertices:
p 0 = 1 , p_0=1, p0=1,
p k = ∏ j = 1 k e − ϕ j , k = 1 , ⋯ , n − 3 , p_k=\prod_{j=1}^ke^{-\phi_j},\ \ k=1,\cdots,n-3, pk=∏j=1ke−ϕj, k=1,⋯,n−3,
θ m = π ∑ k = 0 m − 1 p k ∑ k = 0 n − 3 p k , m = 1 , ⋯ , n − 3 \theta_m=\pi\frac{\sum_{k=0}^{m-1}p_k}{\sum_{k=0}^{n-3}p_k},\ \ m=1,\cdots,n-3 θm=π∑k=0n−3pk∑k=0m−1pk, m=1,⋯,n−3
注: p k = θ k + 1 − θ k θ 1 − θ 0 = θ k + 1 − θ k θ 1 p_k=\frac{\theta_{k+1}-\theta_k}{\theta_1-\theta_0}=\frac{\theta_{k+1}-\theta_k}{\theta_1} pk=θ1−θ0θk+1−θk=θ1θk+1−θk,即第k+1和第k个prevertices的夹角比上第一个和第零个prevertices的夹角。
现在,这个参数问题可以表达为关于无约束变量 ϕ 1 , ⋯ , ϕ n − 3 \phi_1,\cdots,\phi_{n-3} ϕ1,⋯,ϕn−3的一系列方程。本方程组必须使用迭代数值方法求解。注意本系统的雅可比很难解析地表达,大多数情况下使用quasi-Newton迭代或者一些black-box solver可以获得最好的结果。但是,这个方法的复杂度是 O ( n 3 ) O(n^3) O(n3),实际中对于一百个顶点左右问题不大;若有很多顶点,则可以使用简单线性迭代法。**如果定点数很多是因为对平滑的圆弧做了近似,则推荐使用专门应对这种情况下的方法。**参考章节3.6、4.10、4.11。
对于下面两个图(外围是矩形,中间两条狭缝)之间的的变换:两条狭缝必然要move past each other,但是如果长度缩短,则必然导致优化的residual增加,导致系统会收敛到两个狭缝会和的情况。因此,使用梯度下降的方法并不能将左图变换到右图,必须使用某种全局跳跃的方法。在实践中,带有很多凸起或者狭缝的区域会收敛较慢。
_____________ _____________
| | | | | |
| | | | | | | |
|________|__| |____|______|
确定prevertices后,可以通过两个之间的积分来计算常数C,而常数A是积分的base point的映射。
3.2 Quadrature
SC变换要求快速计算 ∫ a b ∏ k = 1 n ( 1 − ζ z k ) α k − 1 d ζ \int_a^b\prod_{k=1}^n(1-\frac{\zeta}{z_k})^{\alpha_k-1}d\zeta ∫ab∏k=1n(1−zkζ)αk−1dζ形式积分的近似。这个积分是路径相关的,我们经常选择线段积分,但在特定情况下其它选项更加合适。因为需要求解参数问题,所以积分的上下界经常是prevertices,而若某顶点内角不是0、180°、360°,则积分有奇点(即平滑函数上的尖点,破坏了平滑性)。
但是,这种奇点的形式可以使用Gauss-Jacobi quadrature求解,它是用于对光滑函数 r ( t ) r(t) r(t)计算 ∫ − 1 1 r ( t ) ( 1 − t ) β ( 1 + t ) γ d t \int_{-1}^1r(t)(1-t)^{\beta}(1+t)^{\gamma}dt ∫−11r(t)(1−t)β(1+t)γdt积分形式的精确方法。通过将积分区间 [ a , b ] [a,b] [a,b]缩放到 [ − 1 , 1 ] [-1,1] [−1,1],并且剔除奇点,可以获得一个光滑的积分。
但是还有问题:如果存在crowding问题,则prevertices离得太近,即其他prevertices可能离积分的区间太近,这种奇点会严重减慢收敛速度。可使用compound Gauss-Jacobi方法应对,其中将积分区间根据"one-half规则"(任何奇点距离积分的细分区间不得小于该区间长度的一半)进行进一步细分。
这种思路在很多需要geometric mesh refinement的问题中都有出现,而经证明,refinement ratio σ = ( 2 − 1 ) / 2 ≈ 1.7 \sigma=(\sqrt{2}-1)/2\approx1.7 σ=(2−1)/2≈1.7为最佳,此时对应将one-half规则中的 1 / 2 1/2 1/2换成 1 / 4.8 1/4.8 1/4.8。这可以将SC Toolbox中有些问题的表现提高10%。
求解参数问题时,重点在于边长,即 ∣ ∫ z j z j + 1 ∏ k = 1 n ( 1 − ζ z k ) α k − 1 d ζ ∣ \left|\int_{z_j}^{z_{j+1}}\prod_{k=1}^n\left(1-\frac{\zeta}{z_k}\right)^{\alpha_k-1}d\zeta\right| ∣∣∣∣∫zjzj+1∏k=1n(1−zkζ)αk−1dζ∣∣∣∣。如果积分是沿着单位圆,则绝对值可以拿进积分内部。
3.3 Inverting the map
求解出SC参数之后,只需计算SC积分即可求出正向映射 w = f ( z ) w=f(z) w=f(z)。求解逆映射 z ( w ) z(w) z(w)没有一般的公式,Trefethen提出了两种策略:
- 对于正向映射 f ( z ) − w = 0 f(z)-w=0 f(z)−w=0进行牛顿迭代。这种方法很有吸引力,因为 f ′ ( z ) f'(z) f′(z)很好算,且平方收敛。但需要有好的starting guess,否则容易发散。
- 对于初值问题(initial-value problem, IVP)进行数值求解: d z d w = 1 f ′ ( z ) , z ( w 0 ) = z 0 \frac{dz}{dw}=\frac{1}{f'(z)}, z(w_0)=z_0 dwdz=f′(z)1,z(w0)=z0。更可靠,但收敛更慢。实践中IVP难以确定 w 0 w_0 w0和 z 0 z_0 z0,因为求解完参数问题之后仅知道顶点和prevertices,而这些点上通常没有导数的定义。求解IVP是最好是从 w 0 w_0 w0开始沿某条直线到一个目标点 w w w,这条线段必须在多边形内部,实践中有个不太美观的方法:先求解单位圆上prevertices之间的一些点的正向映射,再穷举检验线段是否符合要求,但这个步骤的计算量相对IVP/Newton来说还是微不足道。
Trefethen建议结合两种方法:先用IVP solver结合较大的误差容忍度获得一个比较好的初始估计,再用牛顿迭代。
3.4 Cross-ratio 参数问题
前文讲了crowding问题,即纵横比大→prevertices离得近→prevertices附近的导数大→对roundoff误差敏感。
可以改变fundamental domain解决这个问题,即使用条带或者矩形而不是单位圆。这反映了圆或者是半平面对某些目标区域不是一个好的选择。但是长条也不适合T形区域或者H形区域。
因为prevertices的选择有三个自由度,则不同prevertex排列可以映射到同一个多边形中,称每一个排列为一个embedding。当目标区域狭长时,不同的embedding会有不同的crowding区域。为了解决crowding,我们需要一个鲁棒的找到等效embedding 的family的方法。具体来讲,需要1) 对family的简洁的表达方式, 2)Access to family中的locally well-conditioned embeddings。
对于第一个,因为同一个family里的embedding可以通过Mobius变换来互相转换,因此family的表达对Mobius变换必须具有不变性。可以定义 n − 3 n-3 n−3个有序排列的4 prevertices元组的交比(cross ratio) ρ ( a , b , c , d ) = ( d − a ) ( b − c ) ( c − d ) ( a − b ) \rho(a,b,c,d)=\frac{(d-a)(b-c)}{(c-d)(a-b)} ρ(a,b,c,d)=(c−d)(a−b)(d−a)(b−c)。对于圆上逆时针排列的四个点,交比是负实数;且交比对Mobius变换具有不变性。
对于 n − 3 n-3 n−3个4元组的选择,可以选连续的prevertices,但CRDT(cross-ratios of the Delaunay triangulation)算法可以获得很好的表现。
Delaunay triangulation(德劳内三角化)是一种三角剖分 D T ( P ) DT(\mathbf{P}) DT(P),其中 P \mathbf{P} P是平面上的点集,使得P中没有点处于 D T ( P ) DT(\mathbf{P}) DT(P)中任何三角形的外接圆的内部。德劳内三角化最大化了三角形的最小角,即避免出现“极瘦”的三角形。
待续…先跳过3.4剩下的部分和3.5.
3.5 Mapping using cross-ratios
3.6 Software
目前最综合最好用的数值SC软件是SC Toolbox (MATLAB),附录中包含怎么使用它。Trefethen写过SCPACK,是第一个广为使用的SC映射工具包,但只有从单位圆的映射,参数问题仅使用边长formulation。
还有其他软件包:
- DSCPACK: 从环带到多边形双连通区域。
- CAP: 映射到圆弧多边形。
- GEARLIKE: 映射到像齿轮的区域。
还有一些不基于SC映射的共形映射软件包:
- CONFPACK: 对分段光滑边界的但连通区域的Symm’s等式,FORTRAN。显式处理了顶点处的奇点。
- zipper: C语言,实现了Kuhnau插值法,非常快。
- CirclePack: C语言,计算具有特定切关系的一系列圆,可以作为共形映射的近似。
Chapter 4: Variations
SC变换的一个特色是其灵活性,其本质是精确处理角度。SC变换不仅是一种映射,而是一种思考平面中势能理论的视角。
若 f f f将上半平面映射到多边形,则 f ′ f' f′分段常数,因为将直线(实轴)映射到多边形(分段线段)。若 f f f将圆映射到多边形,则 f ′ f' f′不可能分段常数,但如果 g ( z ) g(z) g(z)将原来的区域(单位圆)拉直,则 f ′ / g ′ f'/g' f′/g′有分段性质:
设 f f f将区域 D D D映射到多边形区域 P P P(内角为 π α k \pi\alpha_k παk),而 g g g将 D D D映射到直线,则 f ′ ( z ) g ′ ( z ) = C ∏ k = 1 n [ g ( z ) − g ( z k ) ] α k − 1 \frac{f'(z)}{g'(z)}=C\prod_{k=1}^n[g(z)-g(z_k)]^{\alpha_k-1} g′(z)f′(z)=C∏k=1n[g(z)−g(zk)]αk−1。上式其实是对函数 f ( z ) = h ( g ( z ) ) f(z)=h(g(z)) f(z)=h(g(z))求导的链式法则,而 h h h是标准的上半平面映射。
在本章中,会有多于一个边界成分,这时候就需要一些“拉直”的操作。
4.1 从单位圆映射
单位圆性质很好:各向同性(没有特殊的点),容易设置边界条件,有界(好算)。本章节推到单位圆公式(2.4节)。假设点 − 1 -1 −1不是prevertex。
我们选择将单位圆映射到半平面(左半平面, R e [ z ] < 1 2 Re[z]<\frac{1}{2} Re[z]<21)的Mobius变换作为 g ( z ) g(z) g(z)函数,即 g ( z ) = 1 1 + z g(z)=\frac{1}{1+z} g(z)=1+z1。可得 f ′ ( z ) = C g ′ ( z ) ∏ k = 1 n ( g ( z ) − g ( z k ) ) α k − 1 = C ∏ k = 1 n ( z − z k ) α k − 1 f'(z)=Cg'(z)\prod_{k=1}^n(g(z)-g(z_k))^{\alpha_k-1}=C\prod_{k=1}^n(z-z_k)^{\alpha_k-1} f′(z)=Cg′(z)k=1∏n(g(z)−g(zk))αk−1=Ck=1∏n(z−zk)αk−1
即可得 f ( z ) = A + C ∫ z ∏ k = 1 n ( 1 − ζ z k ) α k − 1 d ζ f(z)=A+C\int^z\prod_{k=1}^n\left(1-\frac{\zeta}{z_k}\right)^{\alpha_k-1}d\zeta f(z)=A+C∫z∏k=1n(1−zkζ)αk−1dζ。
4.2 从条带映射
条带 S = { 0 < I m [ z ] < 1 } S=\{0<Im[z]<1\} S={0<Im[z]<1}的优点是可以用于无限通道,且因为条带是上半平面的log,实轴上的crowding可以分散到条带的边界上。
首先将S映射到有裂缝的半平面: sinh [ π 2 ( z − z k ) ] \sinh\left[\frac{\pi}{2}(z-z_k)\right] sinh[2π(z−zk)]。
后面的略去了…条带映射暂时用不到,后面有用再说…
4.3 从矩形映射
矩形的优点:应用上,电阻总容易从矩形来计算,两组边可以分别设定Dirichlet和纽曼边界条件;数值计算上,可以减轻crowding问题。
如2.5章节中所讲,首先要在多边形P边界上选择四个点,对应矩形顶点,这样把P看做一个广义四边形,而四个点的选择决定了目标矩形的长宽比。
我们已知Jacobi elliptic函数 sn ( z ∣ m ) \text{sn}(z|m) sn(z∣m)将矩形映射到上半平面,将点 − K + i K ′ , − K , K , K + i K ′ -K+iK',-K,K,K+iK' −K+iK′,−K,K,K+iK′分别映射到 − m − 1 / 2 , − 1 , 1 , m 1 / 2 -m^{-1/2},-1,1,m^{1/2} −m−1/2,−1,1,m1/2,其中 m m m是elliptic parameter。因此,有 f ′ ( z ) = C sn ′ ( z ) ∏ k = 1 n ( sn ( z ) − sn ( z k ) ) α k − 1 f'(z)=C\text{sn}'(z)\prod_{k=1}^n(\text{sn}(z)-\text{sn}(z_k))^{\alpha_k-1} f′(z)=Csn′(z)∏k=1n(sn(z)−sn(zk))αk−1。
上式很难计算,并且要显式处理奇点 i K ′ iK' iK′。我们可以首先在条带上找到prevertices,然后移植到矩形。关系:矩形–sn–>上半平面–log–>条带。可以在sn映射后附加一个 ( log z ) / π (\log z)/\pi (logz)/π映射,将矩形四个顶点映射到条带边界上d L + i , i , 0 , L L+i, i, 0, L L+i,i,0,L四个点。因此在矩形上代数分布的点在实轴上指数分布(crowding),但是在条带上仍然是代数分布。
但conformal modulus仍然未知,仍然需要在条带上解决参数问题。求解完参数问题后,即可得到 L L L的值。因此,矩形到多边形的映射,即可分解成矩形到条带,再从条带到多边形的映射。
4.4 外部映射(Exterior maps)
多边形的外部本质上也是个单连通的多边形,因此只需改变顶点的顺序(逆时针改成顺时针),即将jump从 ( 1 − α k ) π (1-\alpha_k)\pi (1−αk)π改成 ( α k − 1 ) π (\alpha_k-1)\pi (αk−1)π就可以了。
剩下的略过…暂时用不到…
4.5 周期性区域与分形
若区域是周期性的,则参数问题可以急剧减小,因prevertices的分布也是周期性的。
剩下的略过。。。
4.6 反射与其他变换
反射可以创建对称的区域,在共形映射中有很多应用。如想映射到双连通对称区域(如字母A),则可以将其对称轴左边(which is 一个单连通区域)映射到一个矩形,再反射。
4.7 黎曼曲面
黎曼曲面是一维复流形。
剩下的略过。。。
4.8 齿轮状区域
**一个齿轮状区域(gearlike region)是一个Jordan区域,其边界由一系列圆心在原点的圆弧和一系列从原点发出的线段构成。**这个形状的内角是 π / 2 \pi/2 π/2的整数倍。
齿轮区域的对数(logarithm)是黎曼曲面,其边界由水平和垂直的线段组成。
内角的平均数是 π \pi π,即 ∑ k = 1 n ( α k − 1 ) = 0 \sum_{k=1}^n(\alpha_k-1)=0 ∑k=1n(αk−1)=0,对应总转角是0度。如果原点就在 P P P的边界上,则只需要一个sheet,然后直接应用普通的SC映射到 log P \log P logP就可以了。
对于一般情况,为了让绕原点计算一圈时增大 2 π i 2\pi i 2πi,应当增加一个极点 z − 1 z^{-1} z−1,即 ( log f ( z ) ) ′ = C z − 1 ∏ k = 1 n ( 1 − z z k ) α k − 1 (\log f(z))'=Cz^{-1}\prod_{k=1}^n\left(1-\frac{z}{z_k}\right)^{\alpha_k-1} (logf(z))′=Cz−1∏k=1n(1−zkz)αk−1。在零点右侧的残差是 C ∏ ( 1 ) α k − 1 = C C\prod(1)^{\alpha_k-1}=C C∏(1)αk−1=C,所以我们选择 C = 1 C=1 C=1。对于exterior map,应当选择 C = − 1 C=-1 C=−1。
由此得到从单位圆映射齿轮状区域的SC公式为 f ( z ) = exp [ A ± ∫ z ζ − 1 ∏ k = 1 n ( 1 − ζ z k ) α k − 1 d ζ ] f(z)=\exp\left[A\pm\int^z\zeta^{-1}\prod_{k=1}^n\left(1-\frac{\zeta}{z_k}\right)^{\alpha_k-1}d\zeta\right] f(z)=exp[A±∫zζ−1∏k=1n(1−zkζ)αk−1dζ]。
我们已经假定了一个条件: f ( 0 ) = 0 f(0)=0 f(0)=0,所以映射还有一个自由度,即单位圆的旋转。因此,在参数问题中需要求解 n − 1 n-1 n−1个未知数。因为 log f \log f logf没有乘积常数C,因此SC的image无法缩放。
映射到齿轮状区域的内容在Pearce[Pea91]中有详尽的描述,软件包也开源了(见章节3.6)。
4.9 双连通区域
暂时略过…
4.10 圆弧多边形
圆弧多边形由有限个圆弧和直线段构成。 这在几何上是一个重大改变,之前的原则也失效了。要对映射重新进行解析地描述,来回到SC映射最初始的思路。
暂时跳了…回来再看
4.11 Curved 边界
暂时跳了…
Chapter 5: Applications
共形映射的一个很著名的应用是拉普拉斯方程,在本章中花了三节来讲。SC映射在应用数学和科学中有应用。
5.1 为什么使用SC映射?
最自然的应用是用来在平面中对于分段常数边界条件求解拉普拉斯方程。
很多人使用简单几何区域的SC映射来获得对于具体应用问题的完全解析解。
电子工程中也常用SC映射,如确定电阻、电容、电势、磁势,都可以通过映射到矩形区域来求解。如果在迭代中需要映射,则可以将迭代过程移入映射中。SC映射还应用于波导、集成电路、硬盘磁头、电机、自动控制、霍尔效应、裂缝检测中。
流体力学也是SC映射的一大应用。
Mesh生成是数值SC映射研究的一大驱动。