采样方法（二）MCMC相关算法介绍及代码实现

0.引子

书接前文，在采样方法（一）中我们讲到了拒绝采样、重要性采样一系列的蒙特卡洛采样方法，但这些方法在高维空间时都会遇到一些问题，因为很难找到非常合适的可采样Q分布，同时保证采样效率以及精准度。
本文将会介绍采样方法中最重要的一族算法，MCMC（Markov Chain Monte Carlo），在之前我们的蒙特卡洛模拟都是按照如下公式进行的：
$$E[f(x)]\approx \frac{1}{m}\sum _{i=1}^{m}f(x_i).x_i\sim p.iid$$
我们的x都是独立采样出来的，而在MCMC中，它变成了
$$E[f(x)]\approx \frac{1}{m}\sum _{i=1}^{m}f(x_i).(x_0,x_1,...,x_m)\sim MC(p)$$
其中的$MC(p)$就是我们本文的主角之一，马尔可夫过程（Markov Process）生成的马尔可夫链（Markov Chain）。

1.Markov Chain（马尔可夫链）

在序列的算法（一·a）马尔可夫模型中我们就说到了马尔可夫模型的马尔可夫链，简单来说就是满足马尔可夫假设
$$P(s_n|s_0,s_1,...,s_{n-1})=P(s_n|s_{n-1})$$
的状态序列，由马尔可夫过程（Markov Process）生成。
一个马尔可夫过程由两部分组成，一是状态集合$\Omega$,二是转移概率矩阵$T$。
其流程是：选择一个初始的状态分布${\pi }_0$，然后进行状态的转移：
$${\pi }_n={\pi }_{n-1}T$$
得到的${\pi }_0,{\pi }_1,{\pi }_2...{\pi }_n$状态分布序列。

注意：我们在这里讲的理论和推导都是基于离散变量的，但其实是可以直接推广到连续变量。

马尔可夫链在很多场景都有应用，比如大名鼎鼎的pagerank算法，都用到了类似的转移过程；
马尔可夫链在某种特定情况下，有一个奇妙的性质：

在某种条件下，当你从一个分布${\pi }_0$开始进行概率转移，无论你一开始${\pi }_0$的选择是什么，最终会收敛到一个固定的分布$\pi$，叫做稳态（steady-state）。
稳态满足条件：
$$\pi =\pi T$$
这里可以参考《LDA数学八卦0.4.2》的例子，非常生动地描述了社会阶层转化的一个例子，也对MCMC作了非常好的讲解

书归正传，回到我们采样的场景，我们知道，采样的难点就在于概率密度函数过于复杂而无法进行有效采样，如果我们可以设计一个马尔可夫过程，使得它最终收敛的分布是我们想要采样的概率分布，不就可以解决我们的问题了么。

前面提到了在某种特定情况下，这就是所有MCMC算法的理论基础Ergodic Theorem：
如果一个离散马尔可夫链$(x_0,x_1...x_m)$是一个与时间无关的Irreducible的离散，并且有一个稳态分布$\pi$,则：
$$E[f(x)]\approx \frac{1}{m}\sum _{i=1}^{m}f(x_i).x\sim \pi$$
它需要满足的条件有这样几个，我们直接列在这里，不作证明：

1.Time homogeneous: 状态转移与时间无关，这个很好理解。
2.Stationary Distribution: 最终是会收敛到稳定状态的。
3.Irreducible: 任意两个状态之间都是可以互相到达的。
4.Aperiodic：马尔可夫序列是非周期的，我们所见的绝大多数序列都是非周期的。

虽然这里要求是离散的马尔可夫链，但实际上对于连续的场景也是适用的，只是转移概率矩阵变成了转移概率函数。

2.MCMC

在上面马尔可夫链中我们的所说的状态都是某个可选的变量值，比如社会等级上、中、下，而在采样的场景中,特别是多元概率分布，并不是量从某个维度转移到另一个维度，比如一个二元分布，二维平面上的每一个点都是一个状态，所有状态的概率和为1! 这里比较容易产生混淆，一定小心。

在这里我们再介绍一个概念：
Detail balance： 一个马尔可夫过程是细致平稳的，即对任意a,b两个状态：
$$\pi (a)T_{ab}=\pi (b)T_{ba}$$细致平稳条件也可以推导出一个非周期的马尔可夫链是平稳的，因为每次转移状态i从状态j获得的量与j从i获得的量是一样的，那毫无疑问最后$\pi T=\pi$.

所以我们的目标就是需要构造这样一个马尔可夫链，使得它最后能够收敛到我们期望的分布$\pi$，而我们的状态集合其实是固定的，所以最终目标就是构造一个合适的T，就大功告成了。

一般来说我们有:
$$\pi (x)=\frac{\tilde{\pi }(x)}{Z}$$
其中$Z$是归一化参数$Z={\Sigma }_{x^{\prime }}\tilde{\pi }(x^{\prime })$，因为我们通常能够很方便地计算分子$\tilde{\pi }(x)$，但是分母的计算因为要枚举所有的状态所以过于复杂而无法计算。我们希望最终采样出来的样本符合$\pi$分布。

2.1.Metropolis

2.1.1原理描述

Metropolis算法算是MCMC的开山鼻祖了，它这里假设我们已经有了一个状态转移概率函数T来表示转移概率，T(a,b)表示从a转移到b的概率(这里T的选择我们稍后再说),显然通常情况下一个T是不满足细致平稳条件的：
$$\pi (a)T(a,b)̸=\pi (b)T(b,a)$$
所以我们需要进行一些改造，加入一项$Q$使得等式成立：
$$\pi (a)T(a,b)Q(a,b)=\pi (b)T(b,a)Q(b,a)$$
基于对称的原则，我们直接让
$$\begin{gathered} Q(a,b)=\pi (b)T(b,a). \\ Q(b,a)=\pi (a)T(a,b). \end{gathered}$$
所以我们改造后的满足细致平稳条件的转移矩阵就是：
$$\begin{array}{rl}{T}^{\prime }(a,b)& =T(a,b)Q(a,b)\\ & =T(a,b)\left(\pi (b)T(b,a)\right)\end{array}$$
在Metropolis算法中,这个加入的这个Q项是此次转移的接受概率，是不是和拒绝采样有点神似。

MCMC采样算法
1.有初始状态$x_0$
2.从t=0,1,2,3开始：

• 根据$T(x|x_t)$采样出$x^{\prime }$
• 以概率$Q(x_t,x^{\prime })=\pi (x^{\prime })T(x^{\prime },x_t)$接受，即$x_{t+1}=x^{\prime }$
• 否则使$x_{t+1}=x_t$

但这里还有一个问题，我们的接受概率Q可能会非常小，而且其中还需要精确计算出$\pi (x^{\prime })$，这个我们之前提到了是非常困难的，再回到我们的细致平稳条件：
$$\pi (a)T(a,b)Q(a,b)=\pi (b)T(b,a)Q(b,a)$$
如果两边同时乘以一个数值，它也是成立的，比如
$$\pi (a)T(a,b)Q(a,b)\ast 10=\pi (b)T(b,a)Q(b,a)\ast 10$$
所以我们可以同步放大Q(a,b)和Q(b,a)，使得其中最大的一个值为1，也就是说:
$$\begin{array}{rl}\bar{Q}(a,b)& =\min \left(1,\frac{Q(a,b)}{Q(b,a)}\right)\\ & =\min \left(1,\frac{\pi (b)T(b,a)}{\pi (a)T(a,b)}\right)\\ & =\min \left(1,\frac{\tilde{\pi }(b)T(b,a)}{\tilde{\pi }(a)T(a,b)}\right)\end{array}$$
这样在提高接受率的同时，因为除式的存在我们还可以约掉难以计算的Z。

Metropolis-Hastings算法
1.有初始状态$x_0$
2.从t=0,1,2,3…开始：

• 根据$T(x|x_t)$采样出$x^{\prime }$
• 以概率$\bar{Q}(a,b)=\min \left(1,\frac{\tilde{\pi }(b)T(b,a)}{\tilde{\pi }(a)T(a,b)}\right)$接受，即$x_{t+1}=x^{\prime }$
• 否则使$x_{t+1}=x_t$

2.1.2.代码实验

我们之前提到状态转移函数T的选择，可以看到如果我们选择一个对称的转移函数，即$T(a,b)=T(b,a)$，上面的接受概率还可以简化为
$$\bar{Q}(a,b)=\min \left(1,\frac{\tilde{\pi }(b)}{\tilde{\pi }(a)}\right)$$
这也是一般Metropolis算法中采用的方法，T使用一个均匀分布即可，所有状态之间的转移概率都相同。
实验中我们使用一个二元高斯分布来进行采样模拟

其概率密度函数这样计算的,x是一个二维坐标：
$$p(x)=\frac{1}{2\pi }{e}^{-{x(0)}^2-{x(1)}^2}$$

def get_p(x):
    # 模拟pi函数
    return 1/(2*PI)*np.exp(- x[0]**2 - x[1]**2)
def get_tilde_p(x):
    # 模拟不知道怎么计算Z的PI，20这个值对于外部采样算法来说是未知的，对外只暴露这个函数结果
    return get_p(x)*20

每轮采样的函数：

def domain_random(): #计算定义域一个随机值
    return np.random.random()*3.8-1.9
def metropolis(x):
    new_x = (domain_random(),domain_random()) #新状态
    #计算接收概率
    acc = min(1,get_tilde_p((new_x[0],new_x[1]))/get_tilde_p((x[0],x[1])))
    #使用一个随机数判断是否接受
    u = np.random.random()
    if u

然后就可以完整地跑一个实验了：

def testMetropolis(counts = 100,drawPath = False):
    plotContour() #可视化
    #主要逻辑
    x = (domain_random(),domain_random()) #x0
    xs = [x] #采样状态序列
    for i in range(counts):
        xs.append(x)
        x = metropolis(x) #采样并判断是否接受
    #在各个状态之间绘制跳转的线条帮助可视化
    if drawPath: 
        plt.plot(map(lambda x:x[0],xs),map(lambda x:x[1],xs),'k-',linewidth=0.5)
    ##绘制采样的点
    plt.scatter(map(lambda x:x[0],xs),map(lambda x:x[1],xs),c = 'g',marker='.')
    plt.show()
    pass

可以看到采样结果并没有想象的那么密集，因为虽然我们提高了接受率，但还是会拒绝掉很多点，所以即使采样了5000次，绘制的点也没有密布整个画面。

2.2.Gibbs Sampling

2.2.1.算法分析

通过分析Metropolis的采样轨迹，我们发现前后两个状态之间并没有特别的联系，新的状态都是从T采样出来的，而因为原始的分布很难计算，所以我们选择的T是均匀分布，因此必须以一个概率进行拒绝，才能保证最后收敛到我们期望的分布。
如果我们限定新的状态只改变原状态的其中一个维度，即
$$x_{new}=(x_t^0,x_t^1,..x_{new}^j..,x_t^n)$$
只改变了其中第j个维度，则有$$\begin{gathered} \pi (x_t)=P(x_t^{-j})\ast P(x_t^j|x_t^{-j}) \\ \pi (x_{new})=P(x_t^{-j})\ast P(x_{new}^j|x_t^{-j}) \end{gathered}$$其中$x^{-j}$表示除了第j元其他的变量。
所以有（以$P(x_t^{-j})$为桥梁作转换很好得到）：
$$\pi (x_t)\ast P(x_{new}^j|x_t^{-j})=\pi (x_{new})\ast P(x_t^j|x_t^{-j})$$

所以我们如果构造这样一个转移概率函数T：
1.如果状态a和b之间只在第j个元上值不同，则是的
$T(a,b)=P(b^{(j)}|a{(-j)}) $
2.否则$T(a,b)=0$

结论很清晰：这样一个转移概率函数T是满足细致平稳条件的，而且和Metropolis里面不同：它不是对称的
我们能够以1为概率接受它的转移结果。

以一个二元分布为例，在平面上：

A只能跳转到位于统一条坐标线上的B,C两个点，对于D，它无法一次转移到达，但是可以通过两次变换到达，仍然满足Irreducible的条件。

这样构造出我们需要的转移概率函数T之后，就直接得到我们的Gibbs采样算法了：

Gibbs Sampling算法
1.有初始状态$x_0$
2.从t=0,1,2,3…开始进行循环采样：

• 将$x_t$复制过来，主要是为了循环采样：$x_{t+1}=x_t$
• 枚举维度j = 0…N，修改每个维度的值：
• • • 使得$x_{t+1}^j\sim P(x^j|x_{t+1}^{-j})$

2.2.2.代码实验

想必大家发现了，如果要写代码，我们必须要知道如何从$P(x^j|x_{t+1}^{-j})$进行采样，这是一个后验的概率分布，在很多应用中是能够定义出函数表达的。

在我们之前实验的场景（二元正态分布），确实也能精确地写出这个概率分布的概率密度函数（也是一个正态分布）。

但退一步想，现在我们只关心一元的采样了，所以其实是有很多方法可以用到的，比如拒绝采样等等。

而最简单的，直接在这一维度上随机采几个点，然后按照它们的概率密度函数值为权重选择其中一个点作为采样结果即可。

代码里这样做的目的主要是为了让代码足够简单，只依赖一个均匀分布的随机数生成器。

def partialSampler(x,dim):
    xes = []
    for t in range(10): #随机选择10个点
        xes.append(domain_random())
    tilde_ps = []
    for t in range(10): #计算这10个点的未归一化的概率密度值
        tmpx = x[:]
        tmpx[dim] = xes[t]
        tilde_ps.append(get_tilde_p(tmpx))
    #在这10个点上进行归一化操作，然后按照概率进行选择。
    norm_tilde_ps = np.asarray(tilde_ps)/sum(tilde_ps)
    u = np.random.random()
    sums = 0.0
    for t in range(10):
        sums += norm_tilde_ps[t]
        if sums>=u:
            return xes[t]

主程序的结构基本上和之前是一样的，

def gibbs(x):
    rst = np.asarray(x)[:]
    path = [(x[0],x[1])]
    for dim in range(2): #维度轮询，这里加入随机也是可以的。
        new_value = partialSampler(rst,dim)
        rst[dim] = new_value
        path.append([rst[0],rst[1]])
    #这里最终只画出一轮轮询之后的点，但会把路径都画出来
    return rst,path

def testGibbs(counts = 100,drawPath = False):
    plotContour()

    x = (domain_random(),domain_random())
    xs = [x]
    paths = [x]
    for i in range(counts):
        xs.append([x[0],x[1]])
        x,path = gibbs(x)
        paths.extend(path) #存储路径
    if drawPath:
        plt.plot(map(lambda x:x[0],paths),map(lambda x:x[1],paths),'k-',linewidth=0.5)
    plt.scatter(map(lambda x:x[0],xs),map(lambda x:x[1],xs),c = 'g',marker='.')
    plt.show()

采样的结果：

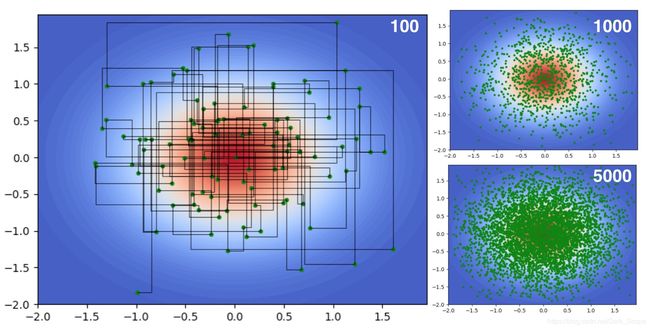
其转移的路径看到都是与坐标轴平行的直线，并且可以看到采样5000词的时候跟Metropolis相比密集了很多，因为它没有拒绝掉的点。

后注

本文我们讲述了MCMC里面两个最常见的算法Metropolis和Gibbs Sampling，以及它们各自的实现，从采样路径来看：

• Metropolis是完全随机的，以一个概率进行拒绝；
• 而Gibbs Sampling则是在某个维度上进行转移。

如果我们仍然希望最后使用独立同分布的数据进行蒙特卡洛模拟，只需要进行多次MCMC，然后拿每个MCMC的第n个状态作为一个样本使用即可。

完整的代码见链接：
https://github.com/justdark/dml/blob/master/dml/tool/mcmc.py
因为从头到尾影响分布的只有get_p()函数，所以如果我们想对其他分布进行实验，只需要改变这个函数的定义就好了，比如说我们对一个相关系数为0.5的二元正态分布，只需要修改get_p()函数：
$$p(x)=\frac{1}{2\pi \sqrt{1-0.5^2}}exp\left(-\frac{1}{2(1-0.5^2)}({x(0)}^2-x(0)x(1)+{x(1)}^2)\right)$$

def get_p(x):
    return 1/(2*PI*math.sqrt(1-0.25))*np.exp(-1/(2*(1-0.25))*(x[0]**2 -x[0]*x[1] + x[1]**2))

就可以得到相应的采样结果：

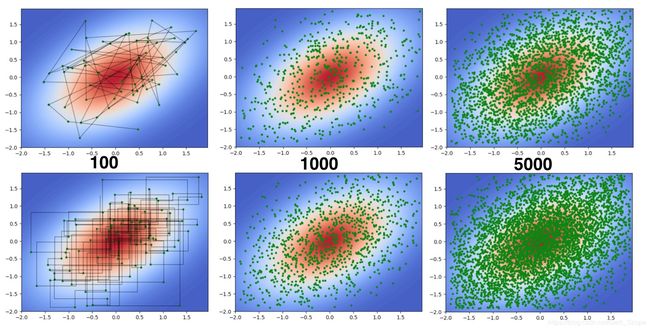
而且因为这里并不要求p是一个归一化后的分布，可以尝试任何>0的函数，比如

def get_p(x):
    return np.sin(x[0]**2 + x[1]**2)+1

也可以得到采样结果：

PPS

终于赶在2017年结束之前填了一个小坑，很久没写博客了。

Reference

【1】LDA数学八卦
【2】Pattern Recognition and Machine Learning
【3】Mathematicalmonk’s machine learning video