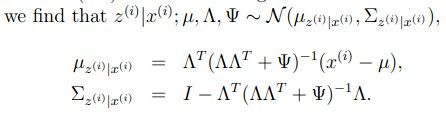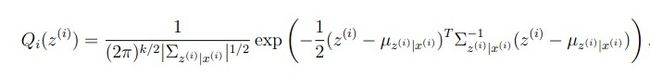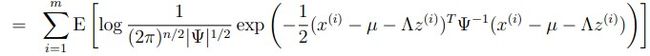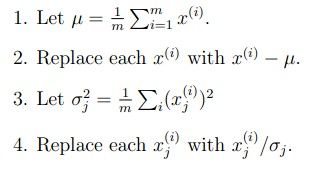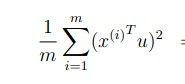机器学习 cs229学习笔记4 (EM for factor analysis & PCA（Principal components analysis）)

=============================================================================

EM FOR FACTOR ANALYSIS

=============================================================================

通过cs229学习笔记3 (EM alogrithm,Mixture of Gaussians revisited & Factor analysis )最后的推导

我们得到了factor analysis model的似然公式：

下面将通过EM算法最大化似然函数：

E-step： 

     我们知道

     通过之前多元高斯分布的条件概率我们可以得到

     

     再将u和Sigma 带回到多元高斯分布的公式里，得到：

    

M-step：

这里我们需要maximize的部分是：(其中的∫……d(z(i))相当于离散数据中的求和符号)

因为p(x(i),z(i))=p( x(i) | z(i) )*p(z(i)) ,所以上式可以化作：（用log函数的性质）

将Qi(z(i))看作是z(i)的概率密度函数，那么积分符号和Qi合起来就是期望的表达式，即上式为：

                          

应为p(z(i))和Qi(z(i))是由已经固定了的高斯分布决定的，所以中括号内的后两项与我们关心的三个参数无关，可以直接省略。

再因为factor analysis的定义，，所以p(x(i) | z(i))=N(μ+∧z,Ψ)，这是多元高斯分布的性质，详细请参看多元高斯分布

所以上式等于：

再用log的性质将公式化简，然后直接使用最大似然估计，就可以得到M-step的参数更新公式了：

提醒一句：Ψ是对角矩阵

========================================================================================

Principal components analysis （PCA）

========================================================================================

这是一个用于降维的算法，先前在coursera上也提到过，至于有什么用处，我们先给出具体的算法吧

在执行PCA之前一般需要将各个参数scalling，使它们的量级相同

大概就是求出平均值，减去平均值，求出方差，除以方差，这样所有参数都在相同的scale上了

然后找到一个响亮，使得所有样例投影到该向量上的距离最短

也就是说：我们需要使下式最大化：

括号内的内容是x(i)映射在u向量上的大小，得到u之后选取前k个u就可以将x降维到k维。

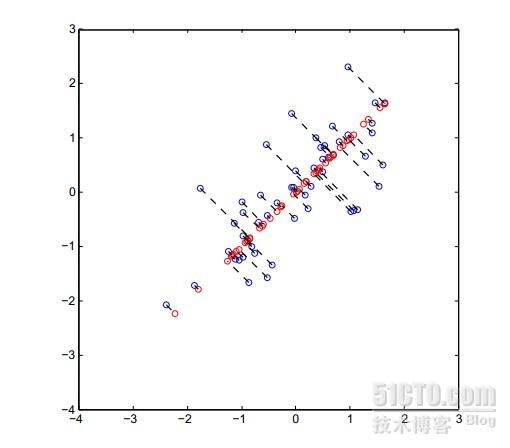
注意u是与红色线相垂直的向量，所以最大化上式也就是最小化点到直线的垂直距离

展示图片是2D-1D，蓝色为原数据点，红色为映射点。可以看出这种方法对数据是有影响的，但是只要在限定范围内，这种影响是可以接受的。

PCA的应用：

1.visualization

  将数据降低到2D或者3D使其可视化

2.compression

  压缩数据

3.Learning

  在learning的过程中可能因为维度过高使其速度变慢，可以用PCA加速，而且实际效果不错

4.anomaly detection

  判断异常，看新点距离子空间是否很大

5.matching/distance calculation

  计算两个样例的距离时不一定是用欧氏距离，而是使用低维中得距离，这样更符合实际，特别是在图像识别中

实例：

  下面是一些人脸图片：

  

上面的图片维度可能较高，比如说100*100，经过PCA之后，可能只是25*25，甚至更低，但仍然很好地捕捉了人脸的形状

在使用pca之后，

  

注意：上面每张图片是单独的一个ui的表示，可以看出还是不错地捕捉了人脸的形状

上面这张图是经过PCA降维后再还原为原维度的图片，可以发现图片虽然有失真，但是失得不多，还是很好的展示了原图像