【机器学习】梯度下降法详解

一、导数

• 导数 就是曲线的斜率，是曲线变化快慢的一个反应。
• 二阶导数 是斜率变化的反应，表现曲线的 凹凸性

$$y=f(x)$$
$$y^{\prime }=f^{\prime }(x)=\frac{dy}{dx}=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

关于导数相关的知识，可参考高等数学

二、偏导数

导数是针对单一变量的，当函数是多变量的，偏导数 就是关于其中一个变量的导数而保持其他变量恒定不变（固定一个变量求导数）。

假定一个二元函数 $z=f(x,y)$，点 $(x_0,y_0)$ 是其定义域内的一个点，将 $y$ 固定在 $y_0$ 上，而 $x$ 在 $x_0$ 上增量 $\Delta x$，相应的函数 $z$ 有增量 $\Delta z=f(x_0+\Delta x,y_0)-f(x_0,y_0)$；$\Delta z$和$\Delta x$的比值当 $\Delta x$ 的值趋向于0的时候，如果极限存在，那么此极限称为函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处对 $x$的偏导数，记作：$f_x^{\prime }(x_0,y_0)$

对 $x$ 的偏导数：
$$\frac{\partial f}{\partial x}|(x=x_0,y=y_0)$$
对 $y$ 的偏导数：
$$\frac{\partial f}{\partial y}|(x=x_0,y=y_0)$$

三、梯度

梯度是一个向量，表示某一函数在该点处的 方向导数 ，沿着该方向取最大值，即函数在该点处沿着该方向变化最快，变化率最大（即该梯度向量的模）；当函数为一维函数的时候，梯度就是导数。

$$\Delta f(x_1,x_2)=(\frac{\partial f(x_1,x_2)}{\partial x_1},\frac{\partial f(x_1,x_2)}{\partial x_2})$$

四、梯度下降法

梯度下降法 常用于求解无约束情况下凸函数的极小值，是一种迭代类型的算法，因为凸函数只有一个极值点，故求解出来的极小值就是函数的最小值点。

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
$${\theta }^{\ast }=arg\underset{\theta }{\min }J(\theta )$$

求解可参考：梯度下降法求解过程

• 梯度下降法的优化思想

用当前位置的 负梯度方向 作为搜索方向，因为该方向为当前位置下降最快的方向，所以梯度下降法也被称为“最速下降法”。梯度下降法中越接近目标值，变化量越小。

计算公式如下（迭代公式）：
$${\theta }^{k+1}={\theta }^k-\alpha \Delta f({\theta }^k)$$

$\alpha$ 被称为步长或者学习率，表示自变量 $x$ 每次迭代变化的大小
收敛条件：当目标函数的函数值变化非常小的时候或者达到最大迭代次数的时候，就结束循环。

五、梯度下降法案例

• 环境
• Anaconda jupyter notebook
• python版本：python3.6

• 导入模块

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from mpl_toolkits.mplot3d import Axes3D

# 设置在jupyter中matplotlib的显示情况
%matplotlib inline

# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

• 一元二次函数

# 一维原始图像
def f1(x):
    return 0.5 * (x - 0.25) ** 2
# 导函数
def h1(x):
    return 0.5 * 2 * (x - 0.25)

# 使用梯度下降法求解
GD_X = []
GD_Y = []
x = 4  # 起始位置
alpha = 0.5  # 学习率
f_change = f1(x)
f_current = f_change
GD_X.append(x)
GD_Y.append(f_current)
iter_num = 0
# 变化量大于1e-10并且迭代次数小于100时执行循环体
while f_change > 1e-10 and iter_num < 100:
    iter_num += 1
    x = x - alpha * h1(x)
    tmp = f1(x)
    f_change = np.abs(f_current - tmp)  # 变化量
    f_current  = tmp  # 此时的函数值
    GD_X.append(x)
    GD_Y.append(f_current)
print(u"最终结果为:(%.5f, %.5f)" % (x, f_current))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X)


# 构建数据
X = np.arange(-4, 4.5, 0.05)  # 随机生成-4到4.5，步长为0.05的数
Y = np.array(list(map(lambda t: f1(t), X)))  # X对应的函数值

# 画图
plt.figure(facecolor='w')
plt.plot(X, Y, 'r-', linewidth=2)  # 函数原图像
plt.plot(GD_X, GD_Y, 'bo--', linewidth=2)  # 梯度跌代图
plt.title(u'函数$y=0.5 * (θ - 0.25)^2$; \n学习率:%.3f; 最终解:(%.3f, %.3f);迭代次数:%d' % (alpha, x, f_current, iter_num))
plt.show()

设置不同的学习率，比较结果：

图中我们可以看出：

• 学习率比较低的时候，不会出现“之”字型
• 学习率过大，结果不收敛，找不到最小值

• 二元函数

# 二维原始图像
def f2(x, y):
    return 0.6 * (x + y) ** 2 - x * y
# 导函数
def hx2(x, y):
    return 0.6 * 2 * (x + y) - y
def hy2(x, y):
    return 0.6 * 2 * (x + y) - x

# 使用梯度下降法求解
GD_X1 = []
GD_X2 = []
GD_Y = []
x1 = 4
x2 = 4
alpha = 0.5
f_change = f2(x1, x2)
f_current = f_change
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(f_current)
iter_num = 0
while f_change > 1e-10 and iter_num < 100:
    iter_num += 1
    prex1 = x1
    prex2 = x2
    x1 = x1 - alpha * hx2(prex1, prex2)
    x2 = x2 - alpha * hy2(prex1, prex2)
    
    tmp = f2(x1, x2)
    f_change = np.abs(f_current - tmp)
    f_current  = tmp
    GD_X1.append(x1)
    GD_X2.append(x2)
    GD_Y.append(f_current)
print(u"最终结果为:(%.5f, %.5f, %.5f)" % (x1, x2, f_current))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X1)


# 构建数据
X1 = np.arange(-4, 4.5, 0.2)
X2 = np.arange(-4, 4.5, 0.2)
X1, X2 = np.meshgrid(X1, X2)
Y = np.array(list(map(lambda t: f2(t[0], t[1]), zip(X1.flatten(), X2.flatten()))))
Y.shape = X1.shape


# 画图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1, X2, Y, rstride=1, cstride=1, cmap=plt.cm.jet)
ax.plot(GD_X1, GD_X2, GD_Y, 'bo--')

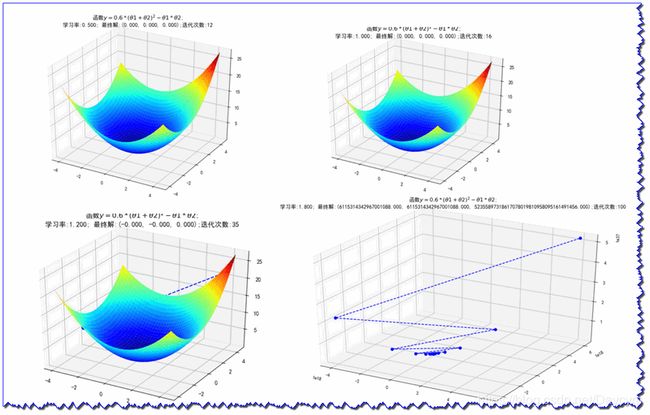
ax.set_title(u'函数$y=0.6 * (θ1 + θ2)^2 - θ1 * θ2$;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f_current, iter_num))
plt.show()

同样设置不同的学习率，比较结果

• 学习率较小时，迭代次数比较小
• 学习率增大，迭代次数增加
• 学习率过大，结果不收敛

六、调优策略

由于梯度下降法中负梯度方向作为变量的变化方向，所以有可能导致最终求解的值是局部最优解，所以在使用梯度下降的时候，一般需要进行一些调优策略：

• 学习率的选择

学习率过大，表示每次迭代更新的时候变化比较大，有可能会跳过最优解；学习率过小，表示每次迭代更新的时候变化比较小，就会导致迭代速度过慢，很长时间都不能结束。

• 算法初始值的选择

初始值不同，最终获得的最小值也有可能不同，因为梯度下降法求解的是局部最优解，所以一般情况下，选择多次不同初始值运行算法，并最终返回函数最小情况下的结果值。

• 标准化

由于样本不同特征的取值范围不同，可能会导致在各个不同参数上迭代速度不同，为了减少特征值的影响，可以将特征进行标准化操作

梯度下降法的常用方法

• 批量梯度下降（BGD）

使用所有样本在当前点的梯度值来对变量参数进行更新操作

更新公式如下：

$${\theta }^{k+1}={\theta }^k-\alpha \sum _{i=1}^m\Delta f_{{\theta }^k}(x^i)$$

• 随机梯度下降法（SGD）

在更新变量参数的时候，随机选取一个样本的梯度值来更新参数

更新公式如下：

$${\theta }^{k+1}={\theta }^k-\alpha \Delta f_{{\theta }^k}(x^i)$$

• 小批量梯度下降法（MBGD）

结合BGD和SGD的特性，从原始数据中，每次选择n个样本来更新参数值，一般n选择10

更新公式如下：

$${\theta }^{k+1}={\theta }^k-\alpha \sum _{i=t}^{t+n-1}\Delta f_{{\theta }^k}(x^i)$$

七、总结

• 对于SGD，由于每次迭代的时候都要对所有的数据集计算求和，计算量就会很大，尤其是训练数据集特别大的时候。此时，我们就可以用随机梯度下降。
• SGD速度比BGD快(迭代次数少)
• SGD在某些情况下(全局存在多个相对最优解/J(θ)不是一个二次)，SGD有可能跳出某些小的局部最优解，所以不会比BGD坏
• BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优解)，SGD由于随机性的存在可能导致最终结果比BGD的差
• 注意：优先选择SGD