各种排序算法的实现

        排序是我们接触Ç编程时，不可避免，不可逾越的一大经典题型

无论是早期接触的冒泡排序，选择排序，桶排序，亦或是后期学习到的希尔排序，

堆排序，快速排序。简言之，排序算法可以说是贯穿我们初学编程的一大算法

         在此，我简单给大家总结一下简单的排序：

• 直接选择排序

先找到第一个数，并设之为最大值，然后将最大与其后的所有数字进行比较，如果该数比最高值要大，则交换这两个数的值，否则继续遍历，直至遍历至最后一个数，一轮比较就结束了，此时，就能在第一个位置上确定最大值

然后找到第二个数，方法同上

......

直至到最后一个数，选择排序也就完成了

代码实现如下：

void SelectSort（int array []，int length）
{
	int i;
	int j;
	int tmp;
	
	for（i = 0; i 
	{
		for（j = i + 1; j 
		{
			if（array [i] 
			{
				tmp = array [i];
				array [i] = array [j];
				数组[j] = tmp;	
			}
		}
	}
	
	printf（“SelectSort complete〜”）;
}

我们发现无论数组的初始状态如何，程序总是要循环执行n * n次，即时间复杂度总为O（n * n）

空间复杂度（辅助存储）O（1）

稳定性，因为算法为逐个遍历，完全忽略了数组可能由相同元素存在的问题，所以不稳定

• 冒泡排序

冒泡冒泡，顾名思义，就是将最大（最小）的数冒上去，依次冒泡，来达到排序的目的

总是比价相邻的元素，如果后者比前者大，则交换两者的元素值

对每一对相邻元素做同样的工作，从第一对做到最后一对，一趟下来，就能确定最大的值（就应该在最后）

然后令遍历的长度减1，重复上述步骤，直至待遍历数组长度为1，说明排序已经完成

（如果在一轮比较之后，没有发生任何元素交换，说明数组已经排序完成，便可终止排序）

void BubbleSort（int array []，int length）
{
	int i;
	int j;
	int tmp;
	int flag = 1;
	
	for（i = length-1; i> 0 && flag == 1; --i）
	{
		flag = 0;
		对于（j = 0; j <++ j）
		{
			if（array [j] 
			{
				flag = 1;
				tmp = array [j];
				array [j] = array [j + 1];
				数组[j + 1] = tmp;
			}
		}
	}
}

时间复杂度：最好的情况是初始数组为有序状态：O（n）的

                    最坏的情况是初始数组为逆向有序，即我们要排序为递增序列，而数组恰好时递减序列：O（N * N）

                    平均复杂度：O（N * N）

空间复杂度（辅助存储）：O（1）

稳定性：因其在元素相同时，两者不会进行无意义的元素交换，所以算法稳定（除非你在写代码时非要在元素相同时还要进行无意义的交换，那么你的算法就是不稳定的了）

• 直接插入排序

插入排序，就是将一个元素插入至数组的合适的位置上，数组仍保持有序状态

比如数组元素：9,8,6,4。我们得到值为7的元素，我们就要找到数组元素中，其前序数比它大，后序数比它小的位置，然后插入该元素

既然是插入元素，数组相对长度总会变长，我们没有办法在数组下标为0处做处理，所以只能在数组末做修改

修改，即扩大数组长度，给新插入的元素腾出位置 

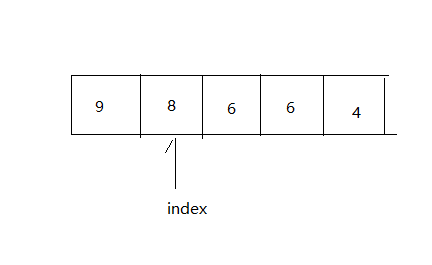
数组由9，8，6，4组成

更新至9，8，7，6，4

我们很容易看到下标为2及其之后的元素都发生了变化，这都是4,6-自知比7小，他们都向后挪动了一格，为即将

插入的7腾出位置，而9,8比7大，所以他们仍在原来的位置

故，直接插入排序的算法为：将7和逆向遍历的数组元素比较，若数组元素比较，若数组元素比移，即数组元素大于7，则：array [index + 1]上的值赋值为7 ,,因为array [index]上的值是比7大的值，所以不能被覆盖掉，反而是array [index + 1]上的值，在先前一次的比较中，已经被赋值给了阵列[指数+ 2]处的元素。

在7找到合适为位置时，数组元素如下：

代码实现如下：

void InsertSort（int array []，int length）
{
	int i;
	int j;
	int tmp;
	
	for（i = 1; i 
	{
		tmp = array [i];
		对于（j = i-1; j> -1 && tmp> array [j];  -  j）
		{
			array [j + 1] = array [j];	
		}
		数组[j + 1] = tmp;
	}
}

时间复杂度：最好情况（数组已经是我们想要的有序状态）：O（n * n）平均情况：O（N * N）

空间复杂度（辅助存储）：O（1）

稳定性：待插入元素一旦找到不小于其的元素时，即刻停止遍历，然后插入（因为继续遍历已经没有意义，都是相同的元素，没有继续遍历的必要）

未完待续......