leetcode试题总结
144. Binary Tree Preorder Traversal
题意:实现二叉树的前序遍历
//iterate 1
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
//iterate 2
class Solution {
private:
stack stk;
vector result;
public:
vector preorderTraversal(TreeNode* root) {
if(!root)
return result;
TreeNode* temp = root;
stk.push(root);
while(!stk.empty())
{
temp = stk.top();
stk.pop();
result.push_back(temp->val);
if(temp->right)
stk.push(temp->right);
if(temp->left)
stk.push(temp->left);
}
return result;
}
}; //iterate 3
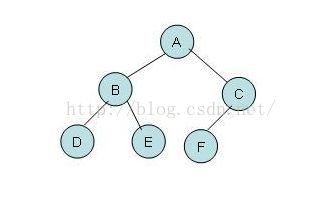
根据先序遍历的顺序,先访问根节点,再访问左子树,后访问右子树,而对于每个子树来说,又按照同样的访问顺序进行遍历,
上图的先序遍历顺序为:ABDECF。非递归的实现思路如下:
对于任一节点P,
1)输出节点P,然后将其入栈,再看P的左孩子是否为空;
2)若P的左孩子不为空,则置P的左孩子为当前节点,重复1)的操作;
3)若P的左孩子为空,则将栈顶节点出栈,但不输出,并将出栈节点的右孩子置为当前节点,看其是否为空;
4)若不为空,则循环至1)操作;
5)如果为空,则继续出栈,但不输出,同时将出栈节点的右孩子置为当前节点,看其是否为空,重复4)和5)操作;
6)直到当前节点P为NULL并且栈空,遍历结束。
下面以上图为例详细分析其先序遍历的非递归实现过程:
首先,从根节点A开始,根据操作1),输出A,并将其入栈,由于A的左孩子不为空,根据操作2),将B置为当前节点,再根据操作1),将B输出,并将其入栈,由于B的左孩子也不为空,根据操作2),将D置为当前节点,再根据操作1),输出D,并将其入栈,此时输出序列为ABD;
由于D的左孩子为空,根据操作3),将栈顶节点D出栈,但不输出,并将其右孩子置为当前节点;
由于D的右孩子为空,根据操作5),继续将栈顶节点B出栈,但不输出,并将其右孩子置为当前节点;
由于B的右孩子E不为空,根据操作1),输出E,并将其入栈,此时输出序列为:ABDE;
由于E的左孩子为空,根据操作3),将栈顶节点E出栈,但不输出,并将其右孩子置为当前节点;
由于E的右孩子为空,根据操作5),继续将栈顶节点A出栈,但不输出,并将其右孩子置为当前节点;
由于A的右孩子C不为空,根据操作1),输出C,并将其入栈,此时输出序列为:ABDEC;
由于A的左孩子F不为空,根据操作2),则将F置为当前节点,再根据操作1),输出F,并将其入栈,此时输出序列为:ABDECF;
由于F的左孩子为空,根据操作3),将栈顶节点F出栈,但不输出,并将其右孩子置为当前节点;
由于F的右孩子为空,根据操作5),继续将栈顶元素C出栈,但不输出,并将其右孩子置为当前节点;
此时栈空,且C的右孩子为NULL,因此遍历结束。代码显示在iterator1,还展示了两种其他的迭代方法,以供参考。
94. Binary Tree Inorder Traversal
题意:实现二叉树的中序遍历
//iterator 1
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
stack stk;
vector result;
public:
vector inorderTraversal(TreeNode* root) {
TreeNode* curNode = root;
while (curNode || !stk.empty())
{
if (curNode->left)
{
stk.push(curNode);
curNode = curNode -> left;
}
else
{
result.push_back(curNode->val);
curNode = curNode->right;
while(!curNode && !stk.empty())
{
curNode = stk.top();
result.push_back(curNode->val);
stk.pop();
curNode = curNode->right;
}
}
}
return result;
}
};
//iterate 2
class Solution {
private:
stack stk;
vector result;
public:
vector inorderTraversal(TreeNode* root) {
TreeNode* curNode = root;
while (curNode || !stk.empty()) {
if (curNode) {
stk.push(curNode);
curNode = curNode -> left;
}
else {
curNode = stk.top();
stk.pop();
result.push_back(curNode -> val);
curNode = curNode -> right;
}
}
return result;
}
}; //iterator 3
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
vector nodes;
std::stack toVisit;
while(1) {
while(root) { toVisit.push(root); root=root->left; }
if(toVisit.empty()) break;
root=toVisit.top(); toVisit.pop();
nodes.push_back(root->val);
root=root->right;
}
return nodes;
}
}; 根据中序遍历的顺序,先访问左子树,再访问根节点,后访问右子树,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的中序遍历顺序为:DBEAFC。非递归的实现思路如下:
对于任一节点P,
1)若P的左孩子不为空,则将P入栈并将P的左孩子置为当前节点,然后再对当前节点进行相同的处理;
2)若P的左孩子为空,则输出P节点,而后将P的右孩子置为当前节点,看其是否为空;
3)若不为空,则重复1)和2)的操作;
4)若为空,则执行出栈操作,输出栈顶节点,并将出栈的节点的右孩子置为当前节点,看起是否为空,重复3)和4)的操作;
5)直到当前节点P为NULL并且栈为空,则遍历结束。
下面以上图为例详细分析其中序遍历的非递归实现过程:
首先,从根节点A开始,A的左孩子不为空,根据操作1)将A入栈,接着将B置为当前节点,B的左孩子也不为空,根据操作1),将B也入栈,接着将D置为当前节点,由于D的左子树为空,根据操作2),输出D;
由于D的右孩子也为空,根据操作4),执行出栈操作,将栈顶结点B出栈,并将B置为当前节点,此时输出序列为DB;
由于B的右孩子不为空,根据操作3),将其右孩子E置为当前节点,由于E的左孩子为空,根据操作1),输出E,此时输出序列为DBE;
由于E的右孩子为空,根据操作4),执行出栈操作,将栈顶节点A出栈,并将节点A置为当前节点,此时输出序列为DBEA;
此时栈为空,但当前节点A的右孩子并不为NULL,继续执行,由于A的右孩子不为空,根据操作3),将其右孩子C置为当前节点,由于C的左孩子不为空,根据操作1),将C入栈,将其左孩子F置为当前节点,由于F的左孩子为空,根据操作2),输出F,此时输出序列为:DBEAF;
由于F的右孩子也为空,根据操作4),执行出栈操作,将栈顶元素C出栈,并将其置为当前节点,此时的输出序列为:DBEAFC;
由于C的右孩子为NULL,且此时栈空,根据操作5),遍历结束。代码如上iterator1所示,同时还给出了几种其他的代码,仅供参考。
145. Binary Tree Postorder Traversal
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
stack stk;
vector result;
public:
vector postorderTraversal(TreeNode* root) {
if(!root)
return result;
stk.push(root);
TreeNode* cur = root;
TreeNode* pre = NULL;
while(!stk.empty())
{
cur = stk.top();
if((cur->left == NULL && cur->right == NULL) || ((pre != NULL) && (pre == cur->left || pre == cur->right)))
{
stk.pop();
result.push_back(cur->val);
pre = cur;
}
else
{
if(cur->right != NULL)
stk.push(cur->right);
if(cur->left != NULL)
stk.push(cur->left);
}
}
return result;
}
}; 根据后序遍历的顺序,先访问左子树,再访问右子树,后访问根节点,而对于每个子树来说,又按照同样的访问顺序进行遍历,上图的后序遍历顺序为:DEBFCA。后序遍历的非递归的实现相对来说要难一些,要保证根节点在左子树和右子树被访问后才能访问,思路如下:
对于任一节点P,
1)先将节点P入栈;
2)若P不存在左孩子和右孩子,或者P存在左孩子或右孩子,但左右孩子已经被输出,则可以直接输出节点P,并将其出栈,将出栈节点P标记为上一个输出的节点,再将此时的栈顶结点设为当前节点;
3)若不满足2)中的条件,则将P的右孩子和左孩子依次入栈,当前节点重新置为栈顶结点,之后重复操作2);
4)直到栈空,遍历结束。
下面以上图为例详细分析其后序遍历的非递归实现过程:
首先,设置两个指针:Cur指针指向当前访问的节点,它一直指向栈顶节点,每次出栈一个节点后,将其重新置为栈顶结点,Pre节点指向上一个访问的节点;
Cur首先指向根节点A,Pre先设为NULL,由于A存在左孩子和右孩子,根据操作3),先将右孩子C入栈,再将左孩子B入栈,Cur改为指向栈顶结点B;
由于B的也有左孩子和右孩子,根据操作3),将E、D依次入栈,Cur改为指向栈顶结点D;
由于D没有左孩子,也没有右孩子,根据操作2),直接输出D,并将其出栈,将Pre指向D,Cur指向栈顶结点E,此时输出序列为:D;
由于E也没有左右孩子,根据操作2),输出E,并将其出栈,将Pre指向E,Cur指向栈顶结点B,此时输出序列为:DE;
由于B的左右孩子已经被输出,即满足条件Pre==Cur->lchild或Pre==Cur->rchild,根据操作2),输出B,并将其出栈,将Pre指向B,Cur指向栈顶结点C,此时输出序列为:DEB;
由于C有左孩子,根据操作3),将其入栈,Cur指向栈顶节点F;
由于F没有左右孩子,根据操作2),输出F,并将其出栈,将Pre指向F,Cur指向栈顶结点C,此时输出序列为:DEBF;
由于C的左孩子已经被输出,即满足Pre==Cur->lchild,根据操作2),输出C,并将其出栈,将Pre指向C,Cur指向栈顶结点A,此时输出序列为:DEBFC;
由于A的左右孩子已经被输出,根据操作2),输出A,并将其出栈,此时输出序列为:DEBFCA;
此时栈空,遍历结束。代码如上面所示。
二叉树的非递归遍历参考http://blog.csdn.net/pi9nc/article/details/13008511文章。
103. Binary Tree Zigzag Level Order Traversal
题意:给定一个二叉树,实现Z字型的层序遍历。例如
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its zigzag level order traversal as:
[
[3],
[20,9],
[15,7]
]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector> zigzagLevelOrder(TreeNode* root) {
vector> result;
if(!root)
return result;
deque tree;
tree.push_back(root);
int flag = 0;
while(!tree.empty())
{
int count = tree.size();
vector level;
while(count-- > 0)
{
TreeNode* pCur = tree.front();
tree.pop_front();
level.push_back(pCur->val);
if(pCur->left)
tree.push_back(pCur->left);
if(pCur->right)
tree.push_back(pCur->right);
}
if(flag & 1)
reverse(level.begin(),level.end());
result.push_back(level);
++flag;
}
return result;
}
}; 总结:咋一看这道题似乎是二叉树的层序遍历,但实际上跟层序遍历还是有点区别的,咱不说输出的格式问题,层序遍历中每层输出的顺序都是从左向右的,但是这里的顺序是间隔的从左向右再从右向左。但这里我们还是可以用层序遍历的思路去做,只不过最后给奇数层的序列的输出反转一下即可。算法思路如下:
层序遍历与前面三个不同的地方是,层序是按照顺序一层一层来遍历的,都是从左结点到右节点的顺序,所以实现层序遍历的结构是队列而不是栈。这里选用STL中的deque结构。
1)从根节点开始,初始先把根节点入队列;
2)如果队列中结点为空,则程序结束;
3) 从队列中取出一节点作为被访问的节点,出列并显示它的数据;并把它非空的左右子树 放到队列中;
4)回到2循环
根据题目的要求,这里添加了一点内容,首先返回的结果是int类型容器的容器。所以需要构建容器的容器类型result以及容器level,因为level每次循环都需要清空,故放在循环内部。count用来指示当前该层拥有的结点数目,每次遍历到某一层,都需要将该层的所有结点全部从队列中弹出。最后的falg变量与1做按位与操作是将所有的奇数层的level中的元素反转。行程Z字形的层序遍历。