最短路算法合集
今天是2017/5/8,DCDCBigBig的第二篇博文
刚开完博客,心情非常的exciting,就先来贴贴代码,讲一些常用的最短路(有时也是最长路)的算法。
floyd
这个算法,额,其实就是暴力吧。n^3的时间复杂度,在任何比赛里都只能是10~30分的做法。废话不多说,先来上代码:
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
edge[i][j]=min(edge[i][j],edge[i][k]+edge[k][j]);
}
}
}在这里edge[i][j]表示在一个图中点i到点j的距离。那么这个算法的思想就是暴力枚举出一个点对(i,j),然后再暴力枚举一个中间点k,对每个k都做一次比较,如果经过k的这条路径小于原先的最短路,那么就更新。
当然,还要判断到底有没有这些边,不过这里省略了。
这个算法其实有一个好,就是很短很好理解,支持多源多汇,基本可以秒背,在比赛时实在不会其它的做法还可以用来水二三十分。
7月13日update:(ps:代码里的i、j、k在循环和数组里的位置千万不要写反!!!平常可能没什么事,但在特殊情况下可能会巨坑!让我NOIP2013换教室那题调了3个小时!!!)
Dijkstra
这个算法也比较基础,大概思想就是贪心,把图中的所有点分成两部分,一部分是已经处理的,一部分是还没处理的,然后每次在当前点找一个离它最近的未处理的点更新即可。见代码:
#includemap[now][j];
}
}
for(int j=1;j<=n;j++){
if(!vis[j]&&sp[j]true;
}
}
int main(){
memset(map,0x7f,sizeof(map));
memset(sp,0x7f,sizeof(sp));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
map[u][v]=w;
}
dijkstra(1);
printf("%d",sp[n]);
return 0;
} 这个算法的时间复杂度很容易可以看出来是O(V^2)的(V代表点数),依然不优。观察思想就可以发现,我们就有一个优化的方法,就是用堆,也就是优先队列来优化,尽量减少比较松弛操作。见代码(邻接表实现):
#includeq;
q.push(point(s,0));
vis[s]=true;
sp[s]=0;
while(!q.empty()){
int u=q.top().id;
q.pop();
vis[u]=true;
for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){
int v=a[tmp].v;
if(!vis[v]&&sp[u]+a[tmp].wint main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
dijkstra(1);
printf("%d",sp[n]);
return 0;
} 熟悉的童鞋可能可以看出,这个代码和SPFA很相似是不是?可它们还是有本质上的区别,想想为什么?
可以看出,这个优化过的版本时间复杂度是O(ElogV),(E代表边数),还是很吼的。
可是无论有没有优化,Dijkstra都有缺陷,就是它不能解决负权边的问题。为什么呢?因为Dijkstra是一个贪心算法,遍历完一遍就不回头再检查是否最优了。考虑下图1:
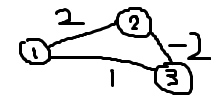
这样跑完之后,你会惊奇的发现答案居然是1而不是0!这是因为Dijkstra在搜到点1后先搜到点3,标记为已处理,不再更新,而实际上最短路是从点2到点3的这条路,但是就搜不到了。那么我们怎么解决负权边的问题呢?
SPFA(Shortest Path Faster Algorithm)
好吧,因为这个算法实在是太有名了,大家一看见就应该能猜出我说的是什么,所以不废话了,先上代码:
void spfa(int vs){
queue<int>q;
bool isin[100001];
int u,v;
memset(isin,0,sizeof(isin));
q.push(vs);
sp[vs]=0;
isin[vs]=true;
while(!q.empty()){
u=q.front();
for(int tmp=h[u];tmp!=-1;tmp=a[tmp].next){
v=a[tmp].v;
if(sp[v]>sp[u]+a[tmp].w){
sp[v]=sp[u]+a[tmp].w;
if(!isin[v]){
q.push(v);
isin[v]=true;
}
}
}
q.pop();
isin[u]=false;
}
}这里的sp数组指的是从源点到其它点的最短路。SPFA其实就是Bellman-Ford(这里就不介绍了,感兴趣的童鞋可以自行百度)的广搜优化版,具体时间复杂度在O(kE)(k一般在2~3之间)到O(VE)间浮动,在期望状态下已经是很优的了。
还是稍微讲一下SPFA的思路吧:在图上跑个广搜,对于当前点找它的所有后继,判断这个后继点的最短路是否大于从当前点到这个后继点的总长度,是的话就更新后继点的最短路。这里要用一个isin数组来记录这个点是否已经在队列中,如果不在就入队。注意一个点可能多次入队(想想为什么?),所以出队时isin要重置为false。
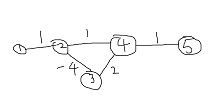
SPFA还有个最好的地方就是可以处理负权边和判断负权环(负权环就是指图中的一个环,它在环中任意一个起点开始走一遍回到自己后路上的权值加起来小于0,具有负权环的图没有最短路),并且十分简单。负权边就不说了,因为这个代码本身就没有贪心的问题。而负权环也很容易判断,怎么搞呢?其实直接判断一个点如对此书是否大于V次就好了。如下图2这个例子,明显在点2-3-4会重复入队,那么只要入队次数超过了点数5,就可以判断出负权环。
其它算法
其实在最短路这个方面,不仅仅有上面的这些算法,这些只是一些常用的模板而已,其实一些很朴素的做法就可以A掉很多题目。比如说普通bfs就可以A掉很多类似于走迷宫的最短路题目。(参考GDOIday2t1RPG,本辣鸡写了个SPFA结果爆炸45pts)所以我们在做题的时候要灵活一点,不能拘泥于几个朴素算法,要学会结合题目来优化、创新。