[详解]STOER-WAGNER算法求解无向图最大流最小割

---

算法思想：

假设s,t是图G中的两个点，把s，t合并为一个点后，得到图G/{s,t}

1. 如果图G的最小割min-cut把s，t点分开，那么s，t的最小割也就是图G的最小割
2. 如果图G的最小割没有把s，t点分开，那么图G/{s,t}的最小割会把s，t点分开

依据这个思想，在图G中任意选择s，t点，循环寻找最小的s-t-cut，就可以找到图G的最小割

---

算法：

1. MinimumCutPhase(G,w,a)

A←{a}
while A ≠ V
    if v ∈ A and v ∉ A and w(A,v) = max { w(A,y) | y∉ A }
          merge A and v （注意:在还剩最后两个点的时候停下来，退出循环）
return cut-of-phase = w(A，last two vertices)

- A是图G的子集，初始化时，任意指定一个点a放入A集合中
- w(A,v)是点v与集合A中所有点之间连线的权重的和
- cut-of-phase是指把A和剩下的最后两个点分割开的cut

2. MinimumCut(G,w,a)

while |V| ＞ 1
    cut-of-phase = MinimumCutPhase(G,w,a)
    if cut-of-phase ＜ current-minimum-cut
         current-minumum-cut = cut-of-phase

-初始化current-minimum-cut为第一个cut-of-phase

如果没看懂算法的话，可以先看看下面的例子，再回过头来理解

---

例子：

————————————–图G如上图所示，各点的权重已给出——————————–

初始化：取点2放入A中：A={2}（也可以选取其他的点，结果没有影响）

Phase1:

在余下的所有点中，点3与A的连接权重最大，取出点3放入A中，A={2,3}，并且合并A,3为一个点(合并之后注意修改其余点与A之间边的权重：比如A={2,3}之后，4与A的权重就变成了4)

在余下的所有点中，点4与A的连接权重最大，取出点4放入A中，A={2,3,4}，并且合并A,4为一个点(合并之后注意修改其余点与A之间边的权重：比如A={2,3,4}之后，w(A,7)=w(A,7)+w(7,4)=2+2=4)

在余下的所有点中，点7与A的连接权重最大，取出点7放入A中，A={2,3,4,7}，并且合并A,7为一个点

在余下的所有点中，点8与A的连接权重最大，取出点8放入A中，A={2,3,4,7,8}，并且合并A,8为一个点

在余下的所有点中，点6与A的连接权重最大，取出点6放入A中，A={2,3,4,6,7,8}，并且合并A,6为一个点

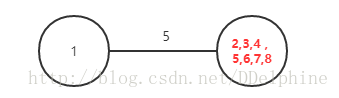
接下来就只剩下两个点1，5。令5为s，1为t（与A边权重较大的为s，较小的为t）
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（s,A）和t
cut-of-phase=5
current-minimum-cut=5

---

phase2:

合并phase1中最后剩下的两个点1和5：

在余下的所有点中，点(1,5)与A的连接权重最大，取出点(1,5)放入A中，A={2,(1,5)}，合并A,(1,5)为一个点

在余下的所有点中，点6与A的连接权重最大，取出点6放入A中，A={2,(1,5),6}，合并A,6为一个点

在余下的所有点中，点3与A的连接权重最大，取出点3放入A中，A={2,(1,5),6,3}，并且合并A,3为一个点

在余下的所有点中，点4与A的连接权重最大，取出点4放入A中，A={2,(1,5),6,3,4}，并且合并A,4为一个点
令剩下的两点中7为s, 8为t
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（s,A）和t
cut-of-phase=5
current-minimum-cut=5

---

phase3:

合并phase2中最后剩下的两个点7和8：

在余下的所有点中，点(1,5)与A的连接权重最大，取出点(1,5)放入A中，A={2,(1,5)}，合并A,(1,5)为一个点

在余下的所有点中，点6与A的连接权重最大，取出点6放入A中，A={2,(1,5),6}，合并A,6为一个点

在余下的所有点中，点3与A的连接权重最大，取出点3放入A中，A={2,(1,5),6,3}，并且合并A,3为一个点
令剩下的两点中4为s, (7,8)为t
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（s,A）和t
cut-of-phase=7
current-minimum-cut=5 (因为当前cut-of-phase > current-minimum-cut)

---

phase4:

合并phase3中最后剩下的两个点4和(7,8)：

在余下的所有点中，点(1,5)与A的连接权重最大，取出点(1,5)放入A中，A={2,(1,5)}，合并A,(1,5)为一个点

在余下的所有点中，点6与A的连接权重最大，取出点6放入A中，A={2,(1,5),6}，合并A,6为一个点
令剩下的两点中3为s, (4,7,8)为t
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（s,t）和A
cut-of-phase=4
current-minimum-cut=4 (因为当前cut-of-phase < current-minimum-cut)

---

phase5:

合并phase4中最后剩下的两个点3和(4,7,8)：

在余下的所有点中，点(1,5)与A的连接权重最大，取出点(1,5)放入A中，A={2,(1,5)}，合并A,(1,5)为一个点
令剩下的两点中6为s, (3,4,7,8)为t
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（A,s）和t
cut-of-phase=4
current-minimum-cut=4

---

phase6:

合并phase5中最后剩下的两个点6和(3,4,7,8)：
令剩下的两点中(3,4,6,7,8)为s, (1,5)为t
如下图所示，很明显此时的s-t最小割s-t-cut应该将图分为（A,s）和t
cut-of-phase=7
current-minimum-cut=4

---

phase7:

合并phase6中最后剩下的两个点(1,5)和(3,4,6,7,8)：
cut-of-phase=9
current-minimum-cut=4

综上，可以看出，图的最小割出现在phase4和phase5，分割结果为{3,4,7,8}，{1,2,5,6}，minumum-cut=4。

---

参考论文A simple Min-Cut Algorithm