一、简述斜率优化
初步了解
本文以luoguP3195 玩具装箱为例,我们很容易可以的出下面这个柿子:
\[ f_i = \min_{j = 1}^{i - 1} \{ f_j + (i - j - 1 + s_i - s_j - L) ^ 2 \} \]
设 \(b_i = s_i + i\),\(j\) 为 \(f_i\) 的最优决策点,则有:
\[ f_i = f_j + (b_i - b_j - (L + 1)) ^ 2 \]
把只与 \(j\) 有关的放在左边:
\[ f_j + b_j + 2 b_j (L + 1) = 2 b_i b_j - b_i ^ 2 - (L + 1) ^ 2 + 2 b_i (L + 1) + f_i \]
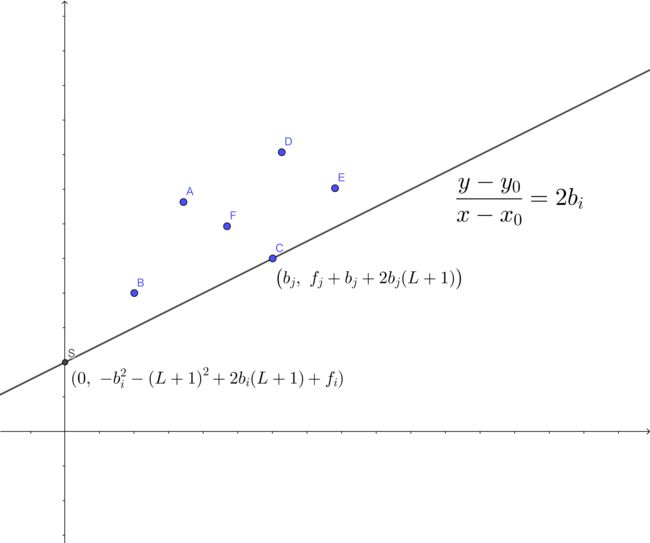
把 \(b_j\) 看做横坐标,\(f_j + b_j + 2 b_j (L + 1)\) 看做纵坐标,这个式子就是一条经过点 \(\big( b_j, f_j + b_j + 2 b_j (L + 1) \big)\),斜率为 \(2 b_i\) 的直线,\(-b_i^2 - (L + 1) ^ 2 + 2 b_i (L + 1) + f_i\) 就看做截距。
由于 \(b_i\) 是确定的,截距中除 \(f_i\) 以外的所有单项式都是常量,所以 \(j\) 是使该直线截距最小的点,可以看成一条斜率为 \(2 b_i\) 的直线从 \(-\infty\) 上移过程中碰到的第一个点。
可以维护一个下凸壳,使直线碰到的第一个点一定在凸壳上。
维护凸壳
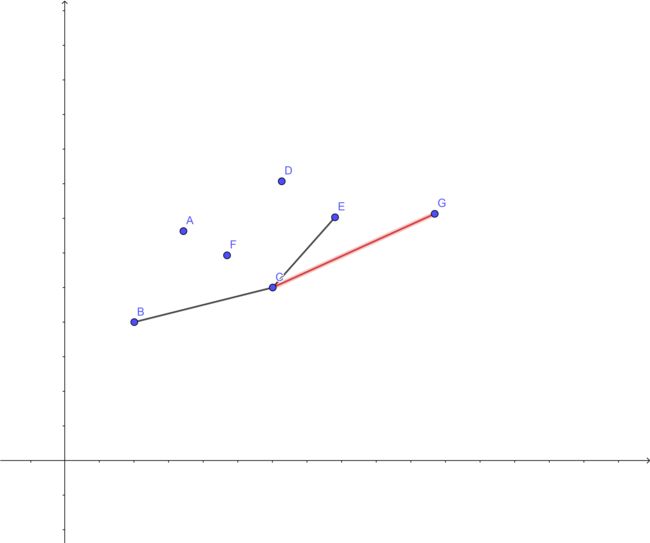
上图中,决策点的下凸壳为 \((B,C,E)\),但因为加入了点 \(G\),点 \(E\) 死了(大雾。
可以得到如下结论:
1、凸壳上边的斜率是从左到右单调递增的,否则会出现上图的情况。
2、设凸壳上的点从左至右依次记为 \(1\)~\(k\),显然有:在凸壳中加入一个横坐标大于当前所有点的点 \(t\),若 \(slope (k - 1, t) \leq slope (k - 1, k)\),则 \(k\) 不在凸壳上。
依照上述做法可以用单调栈来维护凸壳。
找决策点
对于斜率为 \(k\) 的直线,第一个碰到的点为凸壳上第一条斜率小于 \(k\) 的线段右端点,若没有则为最左边的点。
例题中,由于 \(2 b_i\) 的单调性,可以直接用单调队列把不符合上述条件的点扔掉。
一般情况
例题是斜率优化的入门题,当做横坐标和斜率的变量都有单调性,所以很好处理,在更加朴素的情况可以大致分为以下两种:
1、横坐标单调,斜率不单调:不用单调队列,在单调栈上二分即可,或者也可以打平衡树;
2、两者都不单调:我也没写过,平衡树维护应该问题不大。
一些例题
NOI2019d1t1 回家路线
\(Sol\):
记 \(f_i\) 表示乘坐第 \(i\) 班列车到达站点的最小代价。
暴力转移是显然的。
可以把 第\(i\) 班列车看作两个事件:
1、出发时刻:从决策点集中选点决策;
2、到达时刻:把第 \(i\) 个点加入所到达站点的决策点集。
把 \(2m\) 个时间按时间排序,就可以用单调队列维护。
\(p.s.\):由于时间不超过 \(1000\),直接暴力在凸包上选点可过 (考场亲测)。
时间复杂度由于排序可以用 \(vector\)、链表等时间是线性的 \(O(m + T)\),其中 \(T\) 为最大时刻。
\(Source\):
#include
#include
#include
#include
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
templateinline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
templateinline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 1e5 + 5;
struct node {
int x, t;
} a[N << 2];
std::vector q[N], b[2][1001];
int fro[N];
int n, m, A, B, C;
long long f[N << 1];
inline bool chk1(int j, int k, int M) {
return f[j - m] - f[k - m] + A * (a[j].t * a[j].t - a[k].t * a[k].t) > M * (a[j].t - a[k].t);
}
inline bool chk2(int j, int k, int i) {
return (f[j - m] - f[k - m] + A * (a[j].t * a[j].t - a[k].t * a[k].t)) * (a[k].t - a[i].t) >
(f[k - m] - f[i - m] + A * (a[k].t * a[k].t - a[i].t * a[i].t)) * (a[j].t - a[k].t);
}
int main() {
//freopen("in", "r", stdin);
n = in(), m = in(), A = in(), B = in(), C = in();
for (int i = 1, w, x, y, z; i <= m; ++i) {
a[i] = (node){in(), in()};
a[i + m] = (node){in(), in()};
std::swap(a[i].t, a[i + m].x);
b[0][a[i].t].push_back(i), b[1][a[i + m].t].push_back(i + m);
}
memset(f, -1, sizeof(f));
for (int tim = 1, i; tim <= 1000; ++tim) {
for (unsigned p = 0; p < b[0][tim].size(); ++p) {
i = b[0][tim][p];
if (a[i].x == 1)
f[i] = A * a[i].t * a[i].t + B * a[i].t + C;
while ((int)q[a[i].x].size() > fro[a[i].x] + 1) {
int j = q[a[i].x][fro[a[i].x]], k = q[a[i].x][fro[a[i].x] + 1];
if (a[i].t >= a[k].t && chk1(j, k, 2 * A * a[i].t + B))
++fro[a[i].x];
else
break;
}
if ((int)q[a[i].x].size() > fro[a[i].x]) {
int t = q[a[i].x][fro[a[i].x]], tmp = a[i].t - a[t].t;
if (!~f[i])
f[i] = f[t - m] + A * tmp * tmp + B * tmp + C;
else
chk_min(f[i], f[t - m] + A * tmp * tmp + B * tmp + C);
}
}
for (unsigned p = 0; p < b[1][tim].size(); ++p) {
i = b[1][tim][p];
if (~f[i - m]) {
while ((int)q[a[i].x].size() > fro[a[i].x] + 1) {
int j = q[a[i].x][(int)q[a[i].x].size() - 2], k = q[a[i].x][(int)q[a[i].x].size() - 1];
if (chk2(j, k, i))
q[a[i].x].pop_back();
else
break;
}
q[a[i].x].push_back(i);
}
}
}
long long res = -1;
for (int i = 1; i <= m; ++i)
if (a[i + m].x == n && ~f[i])
if (!~res)
res = f[i] + a[i + m].t;
else
chk_min(res, f[i] + a[i + m].t);
printf("%lld\n", res);
return 0;
} updating……