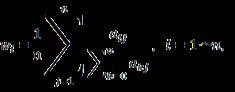2018深圳杯数学建模A题
2018思特奇杯数学建模竞赛题目
(请严格遵守对论文格式的统一要求)
吸引人才最关键的是:符合人才的理想,满足人才的需求和愿望。对大多数人来说,首先关心的是“发展前景”:就业实体及其所在城市的前景,不光当前好,未来也不会很快衰落,毕竟人是要考虑“迁移成本”的;其次是收入(报酬或盈利),这方面有绝对(同行业)的和相对(同地域,平价购买力)的两种考量;再次是环境方面的因素:治安,交通,污染,教育、医疗,购物,等等。目前,这方面定性讨论多,定量研究少;定量研究中单因素的多,综合考虑的少;静态考量多,动态(时变)考量少,考虑“不可比”条件的更少。“少”的原因主要是缺乏合适的“数学模型”,使得结论既缺乏说服力,也缺乏可验证性。
你的团队的任务是:
1、通过收集相关数据、建立数学模型,量化地评价深圳市的人才吸引力水平,并尝试就深圳“加大营商环境改革力度若干措施”对人才吸引力水平的影响做出量化评价。
2.针对具体人才类别,深入分析比较深圳市与其他同类城市(如广州、杭州、厦门、苏州等)在人才吸引力上的优势与不足,给出有效提升人才吸引力的可行方案。
1、《深圳市人民政府印发关于加大营商环境改革力度若干措施》的通知:http://www.sz.gov.cn/zfgb/2018/gb1039/201802/t20180226_10797790.htm
2、深圳市政府信息公开系统网站:http://www.sz.gov.cn/cn/xxgk/zfxxgj/jgsz/
3、深圳市人力资源和社会保障局网站:http://www.szhrss.gov.cn/
4、深圳市南山区人力资源局网站: http://www.szns.gov.cn/xxgk/bmxxgk/qrzj/1. 摘要
本题要解决的是城市人才吸引力水平评价问题。
根据人才的需求,城市人才吸引力水平可以从发展前景,行业增长,收入,环境,政策五个大的方面来衡量。这五个大的方面每个又由若干个小指标构成。全部的小指标共同构成总体的吸引力水平。可以看出,这是一个典型的多要素评价问题,可以构建 层次分析模型进行求解。
在层次分析模型中,对每个要素根据重要性进行排序,构造出判断矩阵。在构造判断矩阵的过程中常常由于人的主观性造成判断矩阵不一致。为避免此问题应该进行一致性检验。对于一致性检验通过的判断矩阵可以根据和法求出各要素的权重。以上的运算都在MATLAB中完成,主要代码在附录中。
利用各要素权重表,将找到的城市的各要素数据带入权重表中即可得到城市的人才吸引力指数。
在模型的检验部分我们算出了上海和深圳的人才吸引力指数。以上海的人才吸引力指数为基准100,可以得到深圳的人才吸引力指数为96。上海的人才吸引力指数比深圳略高,这符合我们的认知,可以据此确定此模型是可靠,可用的。
2.问题重述
人才是城市发展的根本。城市要保证其竞争活力必须有持续的人才流入。要吸引人才,最关键的是这座城市对人才的需求要尽可能满足。按照重要程度,人才的需求可以分为发展前景,收入和环境。发展前景是人才首先考虑的因素。人才流入某一城市,意味着他放弃了原先的发展机会寻找更好的平台,如果新的城市发展前景不够好,某一行业很快衰落,迁移成本大于收益,这是不合算的。收入是人才流动的另一关键因素。收入可以分为绝对收入与相对收入,工资数是绝对输入,而按照所在地区的物价水平,根据工资的购买力水平可以得出相对收入水平。环境因素包括治安、交通、教育、医疗、污染、购物等,这也是人才会考虑的因素。
大多数人才都是根据以上这些因素对城市吸引力作出定性评价。本题要做的就是根据人才的需求,建立数学模型,结合各方面的因素定量的评价城市对人才的吸引力。本题有三个问题:
(1) 根据数学模型及收集的数据,量化的评价深圳市的人才吸引力水平。并就政府的“加大营商环境改革力度若干措施”对人才吸引力的影响作出定量评价。
(2) 针对具体人才类别,分析比较深圳与其他同类城市在人才吸引力上的优势和不足,并给出有效提升人才吸引力的可行方案。
(3) 针对深圳市南山区的经济技术发展特点和相关人才政策,量化地评价深圳南山区人才吸引力水平。
3.模型假设
(1)人才在选择城市的时候,充分了解了该城市的发展前景,收入水平,行业增长率,环境和政府政策等信息。
(2)每个人的选择都是独立的,不受身边的人的影响。
(3)每个人都认为各要素重要程度降序依次为发展前景,收入水平,行业增长率,环境,政策。
4.符号意义
A 判断矩阵
CI 一致性指标
RI 平均随机一致性指标
CR 一致性比例
λmax 矩阵的最大特征值
aij 矩阵A中第i行第j列元素
n 矩阵的阶数
W 权重
5.模型构建
本题要求对城市人才吸引力作出评价。在对一个城市做评价的时候,往往不能只考虑一个方面,要从发展前景,收入和环境等多方面进行评价。在做评价时,这些因素的重要性,影响力或优先程度往往难以量化,人的主观选择会起着相当大的作用。为解决此问题,我们采用了层次分析法,可以定性与定量相结合、系统化、层次化的进行分析。
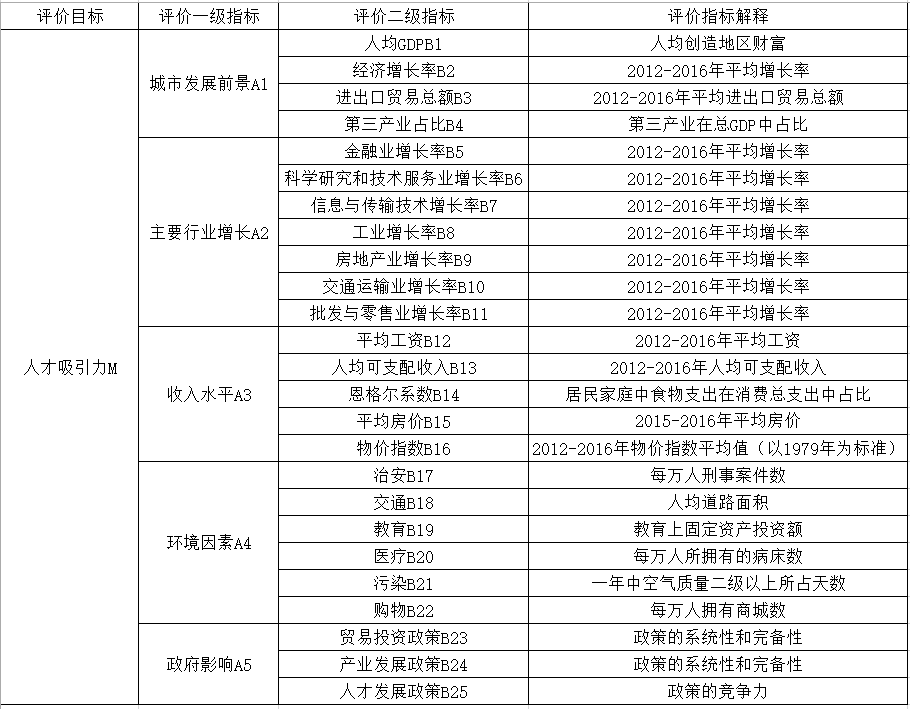
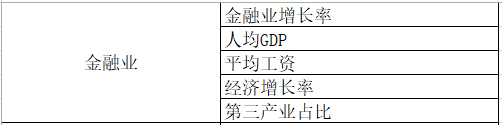
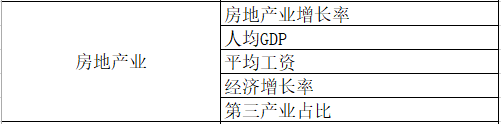
城市人才吸引力水平是城市对人才需求的满足程度的反映。根据题意,人才的需求按照重要程度可以分为发展前景,收入和环境。对此进行调整、细化,我们可以得到人才吸引力评价指标框架。如下表所示:
人才吸引力评价指标原理分析:
(1) 城市发展前景
6.模型求解
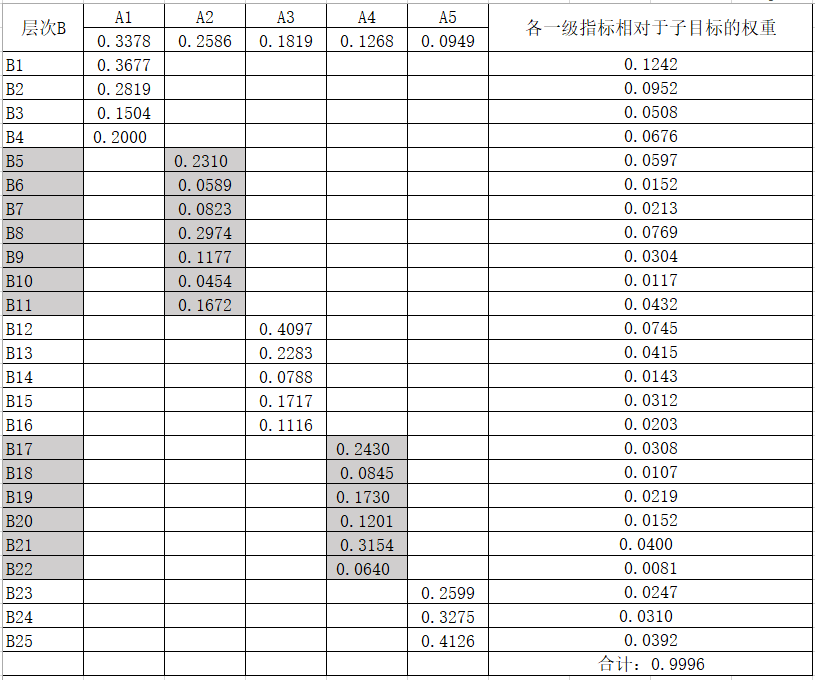
人才吸引力评价指标体系中,各评价指标从不同的方面反映人才吸引力的情况,但它们之间的相对重要程度不同。因此,在建立评价指标体系之后,必须确定各项指标对人才吸引力评价的影响程度。为此,利用层次分析法来确定各指标的权重。
A.求解步骤:
(1) 建立重要程度标度表
在两个要素进行比较时要对它们之间的重要性进行量化,为此建立重要程度标度表,以便比较出它们的优劣及优劣程度。见下表:
xi比xj |
重要性相同 |
稍重要 |
重要 |
很重要 |
绝地重要 |
aij |
1 |
3 |
5 |
7 |
9 |
在每两个等级之间有一个中间状态,aij可分别取值2,4,6,8.
(2) 构造判断矩阵
从层次模型结构的第2层开始,对于从属于上一层每个因素的同一层诸元素,用成对比较法和重要程度标度表构造判断矩阵,只到最下层,格式如下表所示。
M |
A1 |
A2 |
A3 |
A4 |
A5 |
A1 |
… |
… |
… |
… |
… |
A2 |
… |
… |
… |
… |
… |
A3 |
… |
… |
… |
… |
… |
A4 |
… |
… |
… |
… |
… |
A5 |
… |
… |
… |
… |
… |
(3) 对判断矩阵进行一致性检验
在对多个元素进行比较时,人们的判断难以保持完全一致性。为了使对影响因素重要性的比较具有逻辑的一致性,要进行一致性检验。对于每一个判断矩阵计算一致性比例,若一致性比例小于0.1,则检验通过;若不通过,需重新构造判断矩阵。
第一步:计算一致性指标CI
CI=(λmax-n)/(n-1)
将CI作为衡量判断矩阵不一致程度的标准。
第二步:查找相应的平均随机一致性指标RI
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
RI |
0 |
0 |
0.58 |
0.90 |
1.12 |
1.24 |
1.32 |
1.41 |
1.45 |
第三步:计算一致性比例CR
CR=CI/RI
当CR<0.1时,认为判断矩阵是可以接受的;当CR>=0.1时应修改判断矩阵直至达到可接受为止。
(4) 利用和法计算权重向量
取判断矩阵A=(aij)n*n的n个行向量归一化后的算术平均值近似作为权向量,即
B.求解过程
(1)评价目标判断矩阵(相对于评价目标而言,各评价一级指标之间相对重要性的比较)
λmax=5.0915,CI=0.0229,RI=1.12,CR=0.0204<0.1,通过一致性检验
(2)评价一级指标判断矩阵(相对于评价一级指标而言,各评价二级指标之间相对重要性的比较)
城市发展前景
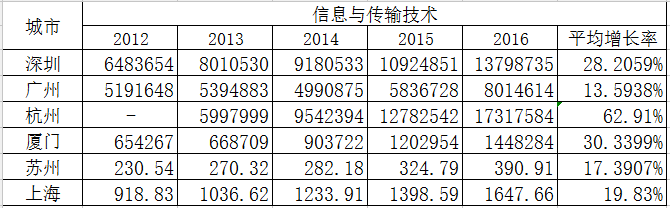
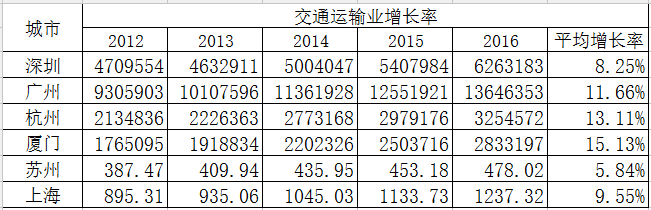
主要行业增长
λmax=7.1018,CI=0.017,RI=1.24,CR=0.0129,CR<0.1,通过一致性检验
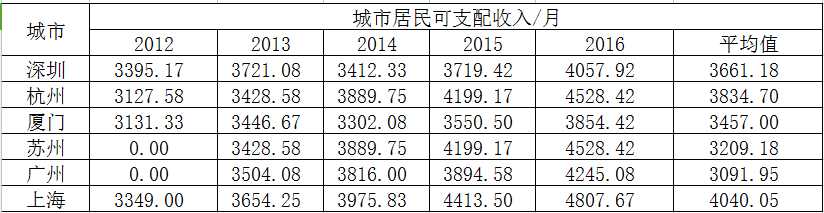
收入水平
λmax=5.1504,CI=0.0376,RI=1.12,CR=0.0336,CR<0.1,通过一致性检验
环境因素
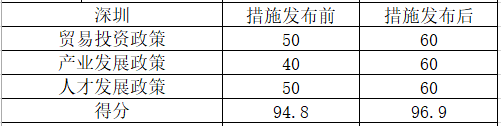
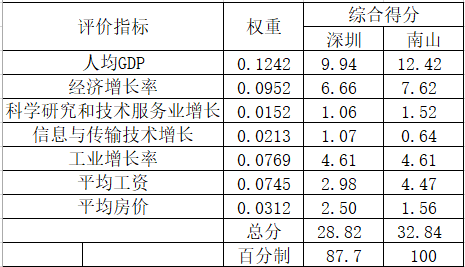
为了对深圳市的人才吸引力水平做出量化评价,我们以上海市为基准建立了参考。通过计算我们可以得出深圳市的城市吸引力指数为70.2,上海市的人才吸引力指数为72.69,见下表。我们以上海的人才吸引力指数为基准100换算可以得出深圳的人才吸引力指数为96.9。
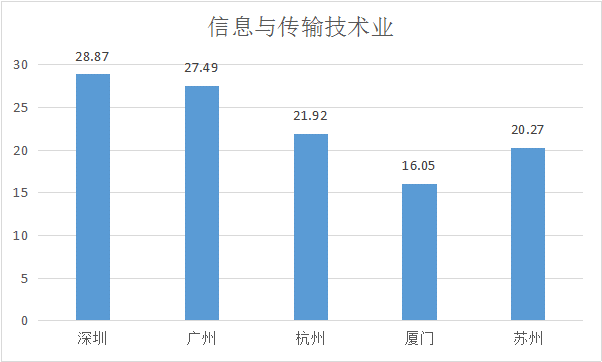
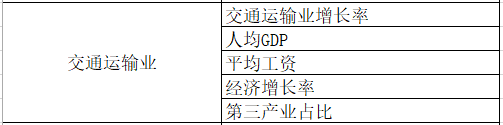
b.科学研究与技术服务业吸引
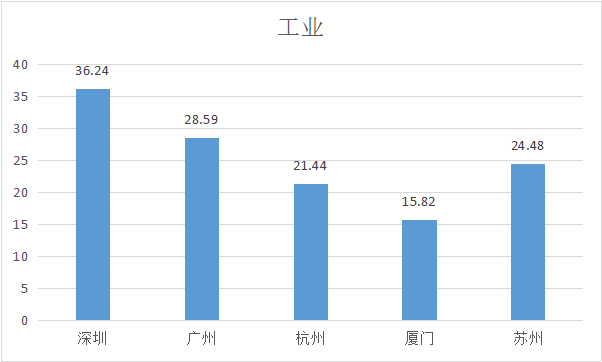
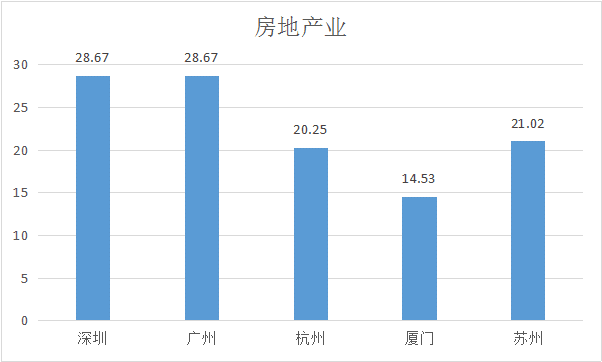
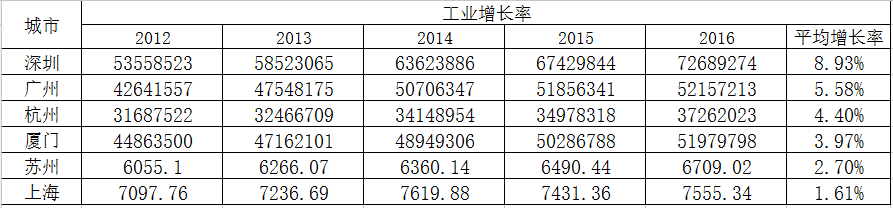
d.工业人才吸引
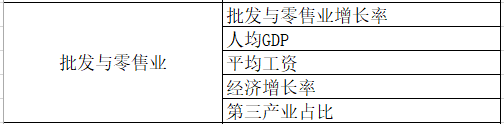
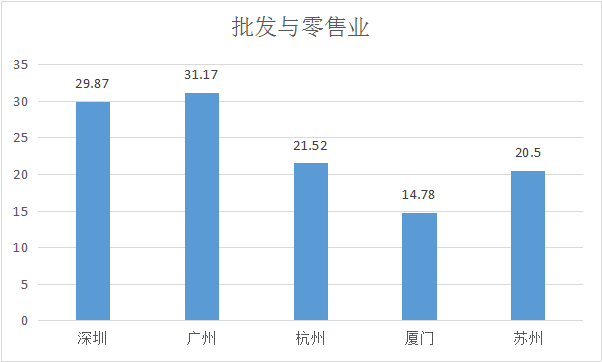
g.批发与零售业人才吸引
7.模型的检验
8.模型的优缺点和改进方向
9.参考文献
[1]中华人民共和国环境保护部,《2016年中国环境状况公报》,http://www.gov.cn/xinwen/2017-06/06/content_5200281.htm,2018年5月1日
[2]深圳市统计局,《深圳统计年鉴2017》、《深圳统计年鉴2016》、《深圳统计年鉴2015》,http://www.sz.gov.cn/tjj/tjsj/tjnj1/,2018年5月1日
[3]杭州市统计局,《2017年杭州统计年鉴》、《2016年杭州统计年鉴》、《2015年杭州统计年鉴》http://www.hangzhou.gov.cn/col/col805741/index.html,2018年5月1日
[4]广州统计局,《广州统计年鉴2017》、《广州统计年鉴2016》、《广州统计年鉴2015》,http://210.72.4.52/gzStat1/chaxun/njsj.jsp,2018年5月1日
[5]苏州统计局,《苏州统计年鉴-2017》、《苏州统计年鉴-2016》、《苏州统计年鉴-2015》,http://www.sztjj.gov.cn/Info.asp?ParentID=64,018年5月1日
[6]上海市统计局,《2017年上海统计年鉴》、《2016年上海统计年鉴》、《2015年上海统计年鉴》http://www.stats-sh.gov.cn/html/sjfb/tjnj/,2018年5月1日
[7]厦门市统计局,《2017年厦门统计年鉴》、《2016年厦门统计年鉴》、《2015年厦门统计年鉴》http://www.stats-xm.gov.cn/tjzl/tjsj/tqnj/,2018年5月1日
[8]刘峰.数学建模.北京:南京大学出版社.2005.
[9]张秀兰.数学建模与实验.北京:化学工业出版社.2013.
[10]王兵团.数学建模基础.北京:清华大学出版社.2004.
function Q=AHP(A)
[m,n]=size(A);
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];
R=rank(A); %求判断矩阵的秩
[V,D]=eig(A); %求判断矩阵的特征值和特征向量,V特征值,D特征向量;
tz=max(D);
B=max(tz); %最大特征值
[row, col]=find(D==B); %最大特征值所在位置
C=V(:,col); %对应特征向量
CI=(B-n)/(n-1); %计算一致性检验指标CI
CR=CI/RI(1,n);
if CR<0.10
disp('CI=');disp(CI);
disp('CR=');disp(CR);
disp('对比矩阵A通过一致性检验,各向量权重向量Q为:');
Q=zeros(n,1);
for i=1:n
Q(i,1)=C(i,1)/sum(C(:,1)); %特征向量标准化
end
else
disp('对比矩阵A未通过一致性检验,需对对比矩阵A重新构造');
end原始数据:
转载请注明本文地址: 2018深圳杯数学建模A题