学习笔记第四十三节：Min_25筛

正题

      听说这个东西是最近几年，某个大佬Min_25提出的，帮助我们解决了许多积性函数前缀和问题。

      为了方便，我们以loj6053:简单的函数一题来讲一讲什么是Min_25筛。

      首先，正如开头所提到的，Min_25筛是用来解决积性函数前缀和问题的。而且，根据我的了解，这个积性函数要满足下面几个性质：1.对于一个质数，一定要是关于p的一个多项式；2.对于一个质数p，满足很好算，（如果不好算的话那么时间复杂度就要乘上这个算的时间复杂度）。

      好我们经过检验，在简单的函数一题中的很明显满足上面的条件。

      因为对于一个大于2的质数p，有。而且很好计算。

       接下来我们要把分开成多个函数相加，使得每一个函数都是完全积性的。

      那么我们可以构造出两个函数然后

      对于每一个先求一个这样的东西：;

      也就是说先把i=质数上的那些数先求出来。

      埃式筛法大家听过吗?就是每次用一个质数去把整个区间筛一下，然后剩下的位子的总和就是我们要求的值。

      但是枚举一个质数p去筛是不现实的，虽说一个质数可以从他的平方倍开始筛起（你考虑一下2这个质数筛一遍的复杂度

      所以我们Dp一下，我们设位前n个数，用了前j个质数进行埃式筛法后的函数值总和。

      显然的如果那么说明它不会再筛去任何一个数，所以。

      那如果不是呢?那么。

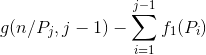      考虑你这个质数会筛掉哪些数，首先是的倍数，然后考虑一下那些的倍数没有被之前除去，相当于，这些倍数有没被之前除去的再减掉质数倍的，因为质数倍的在前面肯定被除去过。又因为是完全积性函数，所以直接乘就可以了，在做题的时候注意边界。同理

      我们求出来了这些g以后。我们在考虑如何算答案。

      首先设表示前n个数中，最小质因子的数的之和。

      那么答案就是。

      。

       首先前面三个式子是算<=n的质数的f(x)值总和，表示的是1到n的质数个数。由于小于的质数不算，所以要减去他们的f值。后面就是枚举一个最小质因子为 ，然后剩下的用大于等于的质数去填，由于是积性函数，所以乘起来就是答案，再加上一个次方即可。

       这里直接递归的时间复杂度就是的，上面求g的时间复杂度也是这个。

       常数不知道，的数据跑了597ms。应该比杜教筛快那么一丢丢，而且这个比杜教筛用途更广。

       有几个之一的地方：

       1.我们筛质数只要筛到就可以了，因为两个东西都是要求的。

       2.如果我递归S的时候没有被筛到呢？这个东西其实不会影响答案，就相当于你只算了前面质数的函数值之和，后面的是不可能递归下去算的。

然后就是代码啦

#include
#include
#include
#include
#include
using namespace std;

long long n;
int m,data;
const long long mod=1e9+7;
bool vis[100010];
int id1[100010],id2[100010];
long long w[100010],g1[100010],g2[100010],sum[100010],p[100010];

void get_prime(){
	data=sqrt(n);
	for(int i=2;i<=data;i++){
		if(!vis[i]) p[++p[0]]=i,sum[p[0]]=(sum[p[0]-1]+i)%mod;
		for(int j=1;i*p[j]<=data;j++){
			vis[i*p[j]]=true;
			if(i%p[j]==0) break; 
		}
	}
}

void get_2g(){
	long long l=1,r,now;
	while(l<=n){
		r=n/(n/l);w[++m]=n/l;
		if(w[m]<=data) id1[w[m]]=m;
		else id2[n/w[m]]=m;
		g1[m]=(w[m]-1)%mod;
		g2[m]=((2+w[m])%mod)*((w[m]-1)%mod)%mod;
		if(g2[m]&1) g2[m]+=mod;g2[m]/=2;
		l=r+1;
	}
	for(int j=1;j<=p[0];j++){
		for(int i=1;i<=m && p[j]*p[j]<=w[i];i++){
			now=w[i]/p[j];
			int id=(now<=data?id1[now]:id2[n/now]);
			g1[i]=(g1[i]-g1[id]+j-1)%mod;(g1[i]+=mod)%=mod;
			g2[i]=(g2[i]-p[j]*(g2[id]-sum[j-1])%mod)%mod;(g2[i]+=mod)%=mod;
		} 
	}
}

long long S(long long x,int y){
	if(x<=1 || p[y]>x) return 0;
	int id=(x<=data?id1[x]:id2[n/x]);
	long long ans=(g2[id]-g1[id]-sum[y-1]+y-1)%mod,p1,p2;(ans+=mod)%=mod;
	if(y==1) (ans+=2)%=mod;
	for(int k=y;k<=p[0] && p[k]*p[k]<=x;k++){
		p1=p[k],p2=p1*p[k];
		for(int e=1;p2<=x;e++,p1=p2,p2*=p[k])
			(ans+=S(x/p1,k+1)*(p[k]^e)%mod+(p[k]^(e+1)))%=mod;
	}
	return ans;
}

int main(){
	scanf("%lld",&n);
	get_prime();get_2g();
	printf("%lld\n",(S(n,1)+1)%mod);
}