提升树入门介绍(Inrtoduction to Boosted Trees)
Author : Jasper Yang
School : Bupt
这是一篇翻译文,翻译的内容是 XGBoost 官网的原理介绍 Introduction to Boosted Trees 这篇文章。
如需转载请注明。我自己在做实验中感觉遇到了瓶颈,我认为是我对这个模型的熟悉度太差,因而需要补一补知识,也希望能帮到大家。
在本文之前给大家推荐一个别人写的关于 XGBoost 参数调优的,还是挺详细的,分享一下 XGBOOST参数调优 。好了,下面就是翻译内容了,可能会夹杂着我自己的理解。
正文
XGBoost 是 极致梯度迭代(这个翻译不知道准不准确)的缩写。梯度迭代这个概念是在 Greedy Function Approximation: A Gradient Boosting Machine, by Friedman 这篇文章中提出来的。XGBoost正是基于这个原始模型。
GBM(boosted trees) 已经出现了有段时日了,在这个话题上有很多的资料。这篇导读希望用监督学习的元素来独立有原则地解释提升树(boosted trees)。
Elements of Supervised Learning (监督学习的元素)
XGBoost 用于解决监督学习的问题,我们用 $ x_{i} $ 去预测 $y_{i}$。在进入树之前,我们先回顾一下监督学习中的基本元素。
Model and Parameters(模型和参数)
监督学习里的模型通常与如何通过$ x_{i} $ 去预测 $y_{i}$的算术结构有关。举例来说,一个线性模型,预测函数是
$$ y^i=\sum_{j}θ_jx_{ij}y^i=\sum_{j}θ_jx_{ij} $$。
预测值可以有基于不同任务的不同的解释(比如,回归或是分类)。举例,当我们需要对输出排序时,可以用逻辑斯蒂转换得到在逻辑回归中正类的概率,也可以把输出值当成排序得分。
参数是我们需要从数据中得到的不确定部分。在线性回归问题中,参数是系数 θ 。通常我们用 θ 来指示参数(在模型中有很多参数,我们的定义十分草率)
Objective Function : Training Loss + Regularization(损失函数:训练误差 + 正则)
基于不同的 $y_i$的理解我们可以有不用的问题,比如回归,分类,排序等等。我们需要找出训练数据最好的参数。为了找出,我们需要定义所谓的损失函数来衡量模型的性能
损失韩式一定需要包括两个部分:训练误差 + 正则。
$$Obj(Θ)=L(θ)+Ω(Θ)$$
L 是训练误差函数,Ω 是正则项。训练误差衡量我们的模型对训练数据的预测的能力。一般来讲是方差,如下(这个使用什么样的误差衡量在参数中可以设置,如均方根-rsme),
$$L(θ)=\sum_{i}(y_i−\hat{y_i})2 $$
另一个常用的损失函数,是逻辑回归函数的逻辑损失函数。
$$L(θ)=\sum_{i}[y_iln(1+e^{−y^i})+(1−y_i)ln(1+e^\hat{y^i})]$$
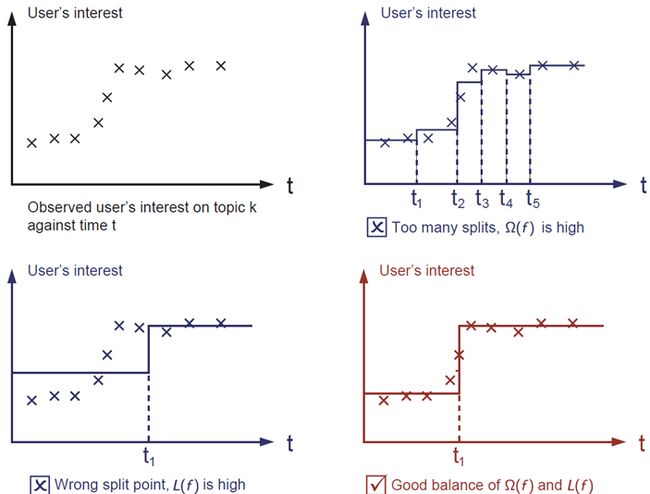
人们经常会忘记加上正则项。正则项控制了模型的复杂程度,能够帮助我们去防止过拟合。这样听起来有点抽象。让我们考虑下图这样一个问题。(我认为过拟合这类东西我们已经滚瓜烂熟了,这里没必要翻译了,这篇文章讲的是有点鸡婆了)
红色的是正确的做法。
Why introduce the general principle?(为什么介绍普遍原理)
上面介绍的东西组成了监督学习的基础元素。(所以说监督学习很简单 :)))我们可以使用上面的原理来衡量提升树和随机森林的不同和公平性。在书面意义上理解原理可以帮助我们学习例如剪枝和平滑这类发散式方法后面的原因。
Tree Ensemble (树的集合)
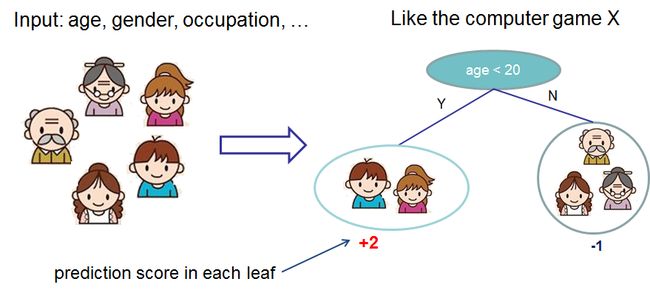
介绍完了监督学习的基本内容,现在让我们开始接触真正的树。开始之前,我们先学习XGBoost的模型:树的集合。一个树集合模型是一个分类回归树(CART)的集合。下面是CART的一个例子,对是否喜欢电脑游戏进行分类。
我们将家庭成员分到不同的叶子节点中,并在相应的叶子节点上赋予得分。一个CART和决策树有些许不同,决策树的叶子结点只有决策值。在 CART 里,最终的得分和每一个叶子结点有关,给予我们一个更加丰富的分类之外的解释。这同时让统一优化的步骤更加容易,在后面我们会见到。
一般来讲,单棵树在现实中不够强大。这就是为什么我们需要能够把多棵树预测值想加的树集合的模型。
上面这是两棵树的树集合的例子。每一棵树的结果想加得到最后的结果。一个重要的因素,两棵树都尝试去补充对方。数学上来讲,我们可以将我们的模型写出如下形式。
$$\hat{y^i}=\sum_{k=1}^{K}f_k(x_i),f_k∈\mathcal{F}$$
K代表树的个数,f是函数空间$mathcal{F}$里的一个函数,$mathcal{F}$是所有可能的 CART 的集合。所以我们优化的目标函数(也就是加了正则后的损失函数)可以写成
$$obj(θ)=\sum_{i}^{n}l(y_i,\hat{y_i})+\sum_{k=1}^{K}Ω(f_k)$$
现在我们有个问题,随机森林的模型是什么样的?就正是树集合!所以随机森林和提升树在模型的形式上没有不同,不同在与我们怎么去训练他们。这意味着你如果写了一个树集合的预测服务,你仅仅需要去实现其中一种并且这个服务随机森林或者提升树下都能运行。
# 这一段我想把英文贴出来,因为我不确定最后两句话我翻译的是否准确
Now here comes the question, what is the model for random forests? It is exactly tree ensembles! So random forests and boosted trees are not different in terms of model, the difference is how we train them. This means if you write a predictive service of tree ensembles, you only need to write one of them and they should directly work for both random forests and boosted trees. One example of why elements of supervised learning rock
Tree Boosting
模型介绍完了,让我们开始真实的训练环节。我们怎么去学习这些树呢?答案和所有的监督学习模型的方法是一样的:定义一个目标函数并优化它
假设我们有如下目标函数。
$$obj=\sum_{i}^{n}l(y_i,\hat{y_i}^{(t)})+\sum_{i=1}^{t}Ω(f_i)$$
Additive Training
我们要问树的参数是什么?你发现我们需要学习的是 $f_i $ 函数(每个都包含了树的结构和叶子得分)。这比起传统的可以用梯度下降解决的优化问题难得多。一下子训练所有的树不太现实。所以我们采用了加和策略:拟合我们已经学习的,然后每一次增加一个新的树。我们把在step t 的预测值写成
$$\hat{y_i}^{(t)}$$
,所以我们得到如下
$$\hat{y}_i^{(0)} = 0$$
$$\hat{y}_i^{(1)} = f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i) $$
$$\hat{y}_i^{(2)} = f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i) $$
$$\dots $$
$$\hat{y}_i^{(t)} = \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)$$
我们还是需要提问:在每一步中,哪一棵树我们需要?最自然的做法是加上一个我们的优化目标。
$$\text{obj}^{(t)} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + constant$$
如果我们使用MSE当我们的损失函数,上式就变成如下形式
$$\text{obj}^{(t)} = \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) $$
$$\quad\quad\quad\quad\quad\quad\quad\quad = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + constant$$
MSE的形式很友好(包含一个一次项,也叫冗余项,和一个二次项)。对于其他的损失函数来说,得到一个好的形式很不容易。所以在大部分的情况下,我们用展开到二级的泰勒展式
$$\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + constant$$
$g_i$和$h_i$定义如下
$$g_i = \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)})$$
$$h_i = \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})$$
当我们把所有的常熟都去除掉后,在step t的特殊的目标函数变成了
$$\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)$$
这变成了我们对新树的目标函数。这样的定义的一个重要的优点是这个方程只依赖于$g_i$和$h_i$。这就是XGBoost怎么支持定制的损失函数。我们用只需$g_i$和$h_i$作为输入的求解程序最优化包括逻辑回归和加权逻辑回归的每一个损失函数。
Model Complexity
我们已经介绍了训练的步骤,但是还有一个重要的事情没提到!就是正则!我们需要定义树的复杂度 Ω(f)。让我们先定义树的方程 f(x)
$$f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\}$$
在这里 w 是叶子结点上得分的向量,q是一个给每个相应叶子结点赋值的方程,以及 T 是叶子结点的数量。在XGBoost中我们定义复杂度如下
$$\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$$
当然,有许许多多的方式去定义复杂度,但这个是在实践中特别有效的一个。正则在很多 的树实现的包里不受重视。这是因为传统的树学习仅仅强调减少杂质。定义了正则后,我们可以更好的知道我们在学习什么。
The Structure Score
这里有关于求导的一个神奇的地方。当我们重新定义树模型后,我们可以把第t棵树的目标函数写成如下
$$Obj^{(t)} \approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$$
$$\quad= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T$$
$I_j = {i|q(x_i)=j}$是对于$q(x_i)=j$的一系列数据点的集合。注意到在第二行我们修改了求和的索引,因为同一个叶子结点上的所有数据有同样的得分。我们可以再次压缩这个方程,定义:
$$G_j = \sum_{i\in I_j} g_i $,$H_j = \sum_{i\in I_j} h_i$$。
$$\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T$$
在这个方程中,$w_j$是相互独立的,
$$G_jw_j+12(H_j+λ)w^2_jG_jw_j+12(H_j+λ)w_j^2 $$
是二次的,在给定q(x)情况下我们能得到的最好的$w_j$和最好的目标函数的减少如下
$$w_j^\ast = -\frac{G_j}{H_j+\lambda}$$
$$\text{obj}^\ast = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T$$
后一个方程衡量了树结构q(x)有多好
如果以上所有听起来有点复杂,让我们看一看这幅图,看看得分是怎么倍计算的。基本上,我们在每个叶子节点上计算$g_i$和$h_i$,将统计累加起来,再使用公式计算得出树的好坏。如果不考虑计算得分中加入了模型复杂度,其实得分就像是在决策树里的不纯度。
Learn the tree structure
现在我们知道怎么去衡量一棵树的好坏了,理想情况下我们会枚举所有可能的树然后选择最好的。但实际上是不可能的,所以我们会尝试去一次优化一个等级。特别是在我们尝试去讲一个叶子结点分成两个叶子是,这个叶子的得分计算为
$$Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma$$
这个公式可以分解成
新的左叶子的得分
新的右叶子的得分
原始叶子的得分
新加的叶子的正则
我们可以观察到一个重要的因素:如果 gain 小于 γ,我们就决定不分叉。这就是基于树模型的剪枝技术。使用了监督学习的原则,我们很自然地想到为什么这个技术能够有效 :)
对于真实值得数据,我们总是想找到最佳的切分。为了有效地达到目的,我们将所有的实例排序,如下图
从左到右的扫描后我们就能得到最可能的切分方式。
Final words on XGBoost
现在你明白了什么事提升树,你也许会问,哪里有XGBoost的文档。 Github 传送门在此,别的不多说了,去实践吧。
翻译的很辛苦,希望能够帮到你们!~
paper done 2017/4/23