数据结构——线性表(一)线性表的顺序存储和单链表
今天,好好整理下线性表的内容,打好基础。同时也为刷程序题做准备。本博客对相关代码做了非常详细的注释。
本博客部分参考了程杰先生的《大话数据结构》和严蔚敏老师的《数据结构c语言版》,以及 牛客网刷题经验帖
1、线性表
线性表(List)是指零个或多个数据元素的有限序列。从名字看,是具有像线一样的性质的表。第一,它是一个序列,也就是说,元素之间是有顺序的,这个顺序不是指从小到大或者从大到小那种顺序,而是指如果元素存在多个,则第一个元素无前驱,最后一个顺序无后继,其它元素都有且只有一个前驱和后继。第二,线性表强调的是有限。利用数学语言定义,如下:
再举几个例子,判断一下是否为线性表。
(1)十二星座。显然是线性表。星座都是以白羊座开头,双鱼座结尾,出起始两个星座以外,其它星座都是有一个直接前驱和直接后继。
(2)公司的组织结构。显然不是,因为一个总经理会管好几个总监,一个总监又会管很多经理,一个员工可能被好几个经理同时管着。所以,对于每一个元素,都不止有一个前驱和一个后继
(3)稍微升级一下:班级的点名册,也是线性表,它是有限序列。这的点名册不止有学生学号、姓名,可能还有出生年月、性别等,这些都是数据项,若干个数据项可以组成一个数据元素。
(4)再升级一下:排队买票,排队的人群属于线性表。但是此时,如果有2个人过来,插在A同学前面,那后面的人肯定不乐意了啊!但是这两个人解释说,A同学手里拿的衣服和书包是他们用来排队的。这不是扯犊子吗?!后面的人肯定不干啊。那照你这么说,我身上的所有东西包括手机鞋帽子都可以排队喽?这肯定是不行的。这说明什么:线性表需要相同的数据类型!那有些人问了,不是看到过用结构体定义一个变量,里面既有 string ,int 还有指针类型啥的吗?请注意,这些东西是数据项,而不是一个数据元素。如果在线性表中的两个结点,他们所包含的数据项内容、类型都是一样的。
2、线性表的抽象数据类型
接下来说一下线性表的抽象数据类型。抽象数据模型(ADT)实际上就是对一种结构进行数学建模,并定义了在该数学模型上的一组操作。这一部分,简单了解一下就行。对线性表的抽象数据类型定义如下:
ADT (List)
Data
Operation
InitList (*L): 初始化线性表L,建立一个空表
ListEmpty(L): 如果线性表为空,返回True,如果非空,返回False
ClearList(*L): 将线性表清空
GetElem(L,i,*e): 将线性表L中的第 i 个元素取出来,用 e 进行保存
LocateElem(L,e): 在线性表L中查找 e ,如果查找成功,返回在表中的位置。否则,返回0 ,表示失败
ListInsert(*L,i,e): 在线性表L中的第 i 个位置插入新元素 e
ListDelete(*L,i,*e):
ListLength(L):
endADT当然了,不同的应用场景,对线性表的基本操作是不同的,上面所列举的是最基本的。对于复杂的操作,完全可以由这些最基本的操作进行组合。
3、线性表的顺序存储结构
线性表有两种物理存储结构:顺序存储和链式存储。所谓顺序存储,指的是用一段连续的存储单元依次存储线性表的数据元素。我们知道,每个数据元素的数据类型都是相同的,我们可以用 C 语言的一维数组实现顺序存储结构,即把线性表的第一个元素存储到数组下标为0的位置,接着依次存储。顺序存储需要三个属性:
(1)线性表的存储位置。数组data,即数组的起始地址;
(2)线性表的最大存储容量。数组长度 MaxSize;
(3)线性表的当前长度。length
代码如下:
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0 // 在if()条件里面,返回 0 代表假
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
ElemType data[MAXSIZE]; // 数组,存储数据元素
int length; // 线性表当前长度
}SqList; // 利用 SqList 就可以定义一个顺序存储的线性表我们可以初始化一个线性表 L;
Status InitList(SqList *L)
{
L->length = 0; // 表长和数据元素个数是有关系的,因此只需要将表长L初始化为 0 即可
return OK;
}这里有几个问题需要强调说明一下:
1)、数组长度和线性表的长度是有区别的
数组的长度表示存储空间的长度,这个量一般是不变的(以后会提到动态分配内存的数组,如 vector)。而线性表的长度表示线性表中数据元素的个数,当有数据被删除或者新的数据元素被插入,线性表的长度都是会变化的。但是,无论怎么变化,线性表的长度都小于等于数组的长度。
2)、地址计算
我们知道,数组的下标是从0开始的,但是,线性表的定义是从 1 开始的,因为我们平时数数的时候,都是从1开始的,所以,线性表的第一个元素是 a1。所以,线性表的第 i 个元素存储在数组下标为 i - 1 的位置。我们用 loc() 来表示存储位置的函数,假设一个数据元素占 n 个存储单元,则第 i 个数据元素 ai 的存储位置可以由 a1 推算出来:
loc(ai) = loc(a1) + (i-1) * n
既然,数据元素在内存中的位置都是可以凭这个公式计算出来的,不管我们要计算的是第一个元素,还是最后一个元素,我们找到它都花费了相同的时间,具有这一特点的存储结构被称为随机存储结构,时间复杂度均为 O(1)。
3.1、顺序存储结构的插入和删除
在进行插入和删除之前,我们需要获得这个元素的位置。在上面定义的抽象数据类型中,有这样一个函数:
GetElem(L,i,*e): 将线性表L中的第 i 个元素取出来,用 e 进行保存即将线性表 L 的第 i 个位置的元素值返回,具体看代码:
Status GetElem(SqList L,int i,ElemType *e)
{
if(L.length==0 || i<1 || i>L.length) // 注意,这里是 . 不是 ->
return ERROR;
*e=L.data[i-1]; //这里为什么把 e 定义为指针呢?其实没必要
return OK;
}注意:
(1)这里的返回值 Status 类型为代表整型,返回 OK 代表 1,返回 ERROR 代表 0。有人会问了,主函数中返回0不是代表执行成功吗?这里为什么会返回 0代表ERROR呢?其实,如果返回值在 if () 函数里面,0 表示 FALSE,非0表示True。
(2)这里 L.length 为什么用 . 而不是-> 呢?是因为 -> 是指针变量指向其成员运算符,而 . 是变量指向其成员的。而这里,为什么 L 的前面一会儿加 * ,一会不加 *呢?我们知道,值传递不能改变变量的值,指针传递才可以,也就是说,如果我们想要改变 L 的值,就需要使用 *L,如果仅仅是读取,可以直接用 L。当然了,所有的 L 前面加上 * ,也是可以的,没问题。
3.1.1 顺序存储的插入
先举个例子,你在火车站排队买票,如果突然冒出个人要在你前面插队,那么,你需要往后退一步,他才能插队。但是,只有你往后退的时候不行,你后面的所有人都得往后退。数据实现过程如图所示:
插入算法的步骤:
(1)如果插入的位置异常,要抛出异常;
(2)如果线性表的长度大于数组的长度,要抛出异常或者动态增加容量;
(3)从最后一个元素开始往前遍历,找到第 i 个位置,分别将他们向后移动一个位置;(从最后面开始遍历,是为了移动时候方便。如果从前面开始遍历,那么移动的时候,还是得将后面的元素全部遍历一遍,显然增加了工作量);
(4)将要插入的元素放到第 i 个位置;
(5)将线性表的表长 +1 (因为要确保,线性表的长度不能大于数组的长度)。
具体代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */
Status ListInsert(SqList *L,int i,ElemType e)
{
int k;
if (L->length==MAXSIZE) /* 顺序线性表已经满 */
return ERROR;
if (i<1 || i>L->length+1)/* 当i比第一位置小或者比最后一位置后一位置还要大时 */
return ERROR;
if (i<=L->length) /* 若插入数据位置不在表尾 */
{
for(k=L->length-1;k>=i-1;k--) /* 将要插入位置之后的数据元素向后移动一位 */
L->data[k+1]=L->data[k]; // 插入的数据,仍然在预先定义的存储空间里
}
L->data[i-1]=e; /* 将新元素插入 */
L->length++;
return OK;
}3.1.2 顺序存储的删除
删除的步骤:
(1)如果删除的位置异常,要抛出异常;
(2)取出删除元素;
(3)从删除的位置往后,遍历剩下的所有元素,分别将他们往前挪一个位置;
(4)将线性表的表长 -1
具体代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */
Status ListDelete(SqList *L,int i,ElemType *e)
{
int k;
if (L->length==0) /* 线性表为空 */
return ERROR;
if (i<1 || i>L->length) /* 删除位置不正确 */
return ERROR;
*e=L->data[i-1];
if (ilength) /* 如果删除不是最后位置 */
{
for(k=i;klength;k++)/* 将删除位置后继元素前移 */
L->data[k-1]=L->data[k];
}
L->length--;
return OK;
} 3.2 插入和删除操作的时间复杂度
先说最好的情况。要插入和删除的位置,恰好在最后一个元素,此时不需要移动元素。所以时间复杂度为O(1);最坏的情况是要插入和删除的位置,恰好在第一个元素,此时需要将每一个元素都移动,所以时间复杂度为 O(n);至于平均情况,对于第 i 个位置,需要移动 n - i 个元素,最终平均移动次数和最中间的那个位置的元素的移动次数相等,为(n-1)/2。所以,平均时间复杂度仍然是 O(n)。
3.3 线性存储结构的优点和缺点
凡是皆有利弊,线性表岂能例外。对于顺序存储结构,优点是不再需要额外增加存储空间;可以快速地存取表中任一位置的元素。缺点是插入和删除需要移动大量的元素;当线性表长度变化较大时,难以确定存储空间的大小。
下面是一个完整的程序,在主程序中,我们一次测试了初始化、插入、删除等操作
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
Status visit(ElemType c)
{
printf("%d ", c);
return OK;
}
typedef struct
{
ElemType data[MAXSIZE]; /* 数组,存储数据元素 */
int length; /* 线性表当前长度 */
}SqList;
/* 初始化顺序线性表 */
Status InitList(SqList *L)
{
L->length = 0;
return OK;
}
/* 初始条件:顺序线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */
Status ListEmpty(SqList L)
{
if (L.length == 0)
return TRUE;
else
return FALSE;
}
/* 初始条件:顺序线性表L已存在。操作结果:将L重置为空表 */
Status ClearList(SqList *L)
{
L->length = 0;
return OK;
}
/* 初始条件:顺序线性表L已存在。操作结果:返回L中数据元素个数 */
int ListLength(SqList L)
{
return L.length;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:用e返回L中第i个数据元素的值,注意i是指位置,第1个位置的数组是从0开始 */
Status GetElem(SqList L, int i, ElemType *e)
{
if (L.length == 0 || i<1 || i>L.length)
return ERROR;
*e = L.data[i - 1];
return OK;
}
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 */
/* 若这样的数据元素不存在,则返回值为0 */
int LocateElem(SqList L, ElemType e)
{
int i;
if (L.length == 0)
return 0;
for (i = 0; i= L.length)
return 0;
return i + 1;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */
Status ListInsert(SqList *L, int i, ElemType e)
{
int k;
if (L->length == MAXSIZE) /* 顺序线性表已经满 */
return ERROR;
if (i<1 || i>L->length + 1)/* 当i比第一位置小或者比最后一位置后一位置还要大时 */
return ERROR;
if (i <= L->length) /* 若插入数据位置不在表尾 */
{
for (k = L->length - 1; k >= i - 1; k--) /* 将要插入位置之后的数据元素向后移动一位 */
L->data[k + 1] = L->data[k];
}
L->data[i - 1] = e; /* 将新元素插入 */
L->length++;
return OK;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */
Status ListDelete(SqList *L, int i, ElemType *e)
{
int k;
if (L->length == 0) /* 线性表为空 */
return ERROR;
if (i<1 || i>L->length) /* 删除位置不正确 */
return ERROR;
*e = L->data[i - 1];
if (ilength) /* 如果删除不是最后位置 */
{
for (k = i; klength; k++)/* 将删除位置后继元素前移 */
L->data[k - 1] = L->data[k];
}
L->length--;
return OK;
}
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:依次对L的每个数据元素输出 */
Status ListTraverse(SqList L)
{
int i;
for (i = 0; i= k; j--)
{
i = ListDelete(&L, j, &e); /* 删除第j个数据 */
if (i == ERROR)
printf("删除第%d个数据失败\n", j);
else
printf("删除第%d个的元素值为:%d\n", j, e);
}
printf("依次输出L的元素:");
ListTraverse(L);
j = 5;
ListDelete(&L, j, &e); /* 删除第5个数据 */
printf("删除第%d个的元素值为:%d\n", j, e);
printf("依次输出L的元素:");
ListTraverse(L);
//构造一个有10个数的Lb
SqList Lb;
i = InitList(&Lb);
for (j = 6; j <= 15; j++)
i = ListInsert(&Lb, 1, j);
unionL(&L, Lb);
printf("依次输出合并了Lb的L的元素:");
ListTraverse(L);
return 0;
} 4、线性表的链式存储结构
前一小节讲到,线性表顺序存储结构的最大缺点就是,插入和删除需要移动大量大元素。那么,为什么会移动大量的元素呢?是因为顺序存储的元素之间的存储位置具有相邻关系:它们在内存中的位置之间没有空隙,自然也就无法快速插入一个元素。而对于删除操作,当中又会空出一些位置,这些位置又需要依靠移动元素来填补。那么如何解决呢?那就是让元素的物理存储之间没有相邻关系,也就是接下来要说的线性表的链式存储结构。
4.1 链式存储的定义
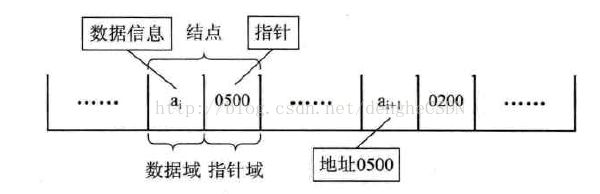
在链式存储中,除了要存储数据元素信息,还要存储它后继元素的存储地址。因此,对于数据元素 ai 来说,除了存储本身的信息以外,还需要存储指示其直接后继的信息(也就是下一个元素的存储位置)。我们把存储数据元素信息的域成为数据域,存储后继位置的域成为指针域,指针域存储的信息称为指针或者链。这样,数据+指针构成了元素 ai 的存储映像,称之为结点。
n 个节点链接成一个链表,即为线性表的链式存储结构。
4.2 单链表
如果链表的每个结点中只包含一个指针域,就叫单链表。如下图所示。
对于线性表,肯定要有头有尾,链表也不例外。我们把链表第一个节点的存储位置称为头指针。整个链表的存取必须从头指针开始进行,之后的每一个结点,其实就是上一个结点的指针指向的位置。那么,最后一个结点的指针指向哪儿呢?它后面已经没有结点了。我们规定,链表最后一个结点指针为空,即 NULL,我们也说,最后一个结点的指针指向空。
有时,为了更加方便对链表进行操作,我们会在链表的第一个结点之前设置一个新的结点,称为头结点。头结点的数据域可以不存储任何信息,指针域存储的是第一个结点的地址。设置头结点为什么会让操作更方便呢?我们在后文会详细叙述。
头结点和头指针的异同点如下:
头指针:1)头指针是指向链表第一个结点的指针,如果链表有头结点,则是指向头结点的指针; 2)头指针具有标识作用,所以常用头指针作为链表的名字; 3)头指针是链表的必须要素,不管链表是否为空,头指针不能为空。
头结点: 1)头结点不是链表的必要元素; 2)头结点是为了操作方便而设立的,放在第一个元素的结点之前,数据域一般是无意义的(有时可以存放链表长度);
有了头结点,对在第一个元素结点之前插入元素,或者删除第一个结点,操作和其它结点就一致了。带有头结点的单链表的结构如下图所示。
单链表的存储结构可以用下面语言描述。代码如下:
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType;/* ElemType类型根据实际情况而定,这里假设为int */
typedef struct Node
{
ElemType data;
struct Node *next;
}*LinkList;
//typedef struct Node *LinkList; /* 定义LinkList *//* 初始化顺序线性表 */
Status InitList(LinkList *L)
{
*L = (LinkList)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */
if (!(*L)) /* 存储分配失败 */
return ERROR;
(*L)->next = NULL; /* 指针域为空 */ //也就是第一个结点为空
return OK;
}
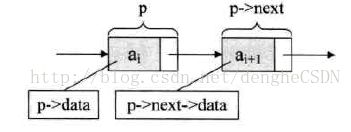
从定义中可以看出,结点由存储数据元素的数据域 + 存放后继结点的地址的指针域组成。假设 p 是指向线性表第 i 个元素的指针,即 p 指向结点 ai ,则 ai 的数据域可表示成 p->data; ai 的指针域可表示成 p->next;p->next的值是一个地址,指向 ai+1 的指针,即指向结点 ai+1有时候,指针所表示的含义是略有不同的,一般来说,我们不说地址,说成指针),也就是说 p->next->data = ai+1 ;如下图所示:
4.3 单链表的遍历
Status GetElem(LinkList L, int i, ElemType *e)
{
int j;
LinkList p; /* 声明一结点p */
p = L->next; /* 让p指向链表L的第一个结点 */
j = 1; /* j为计数器 */
while (p && jnext; /* 让p指向下一个结点 */
++j;
}
if (!p || j>i)
return ERROR; /* 第i个元素不存在 */
*e = p->data; /* 取第i个元素的数据 */
return OK;
} 4.4 单链表的插入
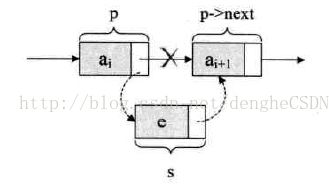
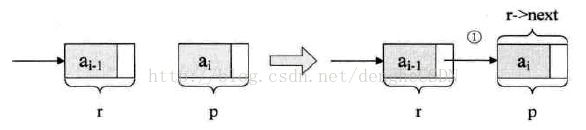
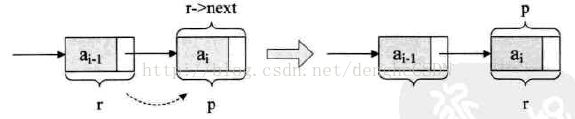
此时,不需要其它结点的参与,只需要调整指针的指向即可。
s->next = p->next;
p->next = s;这两句代码是不可以调换顺序的。因为我们要确保不能“断链”。如果先让 p 指向 s ,那么,ai 结点原来后面的那个结点 ai+1 就无法找到了。同样地,对于表头和表尾的情况,操作是相同的。如下图所示。
单链表在第 i 个数据出插入结点的算法思路为:
(1)定义一个结点 p 指向链表的第一个结点。初始化计数器 j = 1;
(2)当 j
(3)若到了链表末尾,p 为空,则说明第 i 个元素不存在;
(4)否则,查找成功。在程序中生成一个空的结点 s ,将数据元素 e 赋值给 s-> data;
(5)利用单链表的标准插入语句:s->next = p->next;p->next = s;
(6)返回成功。
实现代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
int j;
LinkList p, s;
p = *L;
j = 1;
while (p && j < i) /* 寻找第i个结点 */
{
p = p->next;
++j;
}
if (!p || j > i)
return ERROR; /* 第i个元素不存在 */
s = (LinkList)malloc(sizeof(Node)); /* 生成新结点(C语言标准函数) */
s->data = e;
s->next = p->next; /* 将p的后继结点赋值给s的后继 */
p->next = s; /* 将s赋值给p的后继 */
return OK;
}4.5 单链表的删除
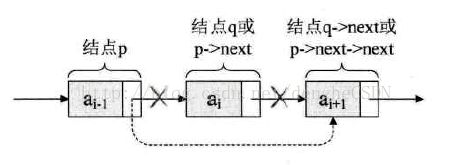
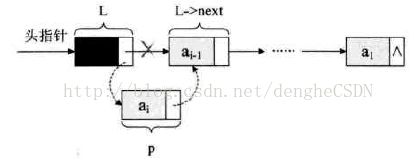
单链表的删除,删除结点 q ,实际就是让 q 结点的前继结点直接指向 q 结点的后继指针。如下图所示。
实际上,执行一步就可以
p->next = p->next->next;为了增加代码的可读性,玲结点 q 来取代 p->next;即
q = p->next;
p->next = q->next;单链表的第 i 个数据删除结点的算法步骤:
(1)定义一个结点 p 指向链表的第一个结点。初始化计数器 j = 1;
(2)当 j
(3)若到了链表末尾,p 为空,则说明第 i 个元素不存在;
(4)否则,查找成功。将要删除的结点 p->next 赋值给 q;
(5)执行删除语句:p->next = q->next;
(6)将被删除的结点 q 的数据赋值给 e ,作为返回值。然后释放 q 结点;
(7)返回成功。
代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */
Status ListDelete(LinkList *L, int i, ElemType *e)
{
int j;
LinkList p, q;
p = *L;
j = 1;
while (p->next && j < i) /* 遍历寻找第i个元素 */
{
p = p->next;
++j;
}
if (!(p->next) || j > i)
return ERROR; /* 第i个元素不存在 */
q = p->next;
p->next = q->next; /* 将q的后继赋值给p的后继 */
*e = q->data; /* 将q结点中的数据给e */
free(q); /* 让系统回收此结点,释放内存 */
return OK;
}总结:单链表的插入和删除算法,都是由两部分组成:1)遍历查找第 i 个元素;2)执行插入和删除语句。从整个算法的角度来看,它们的时间复杂度都是 O(n)。这样看来,单链表的链式存储和顺序存储好像没啥区别。但是,如果我们要在第 i 个位置插入 100 个数据,对于顺序存储,每一次插入都要移动 n-i 个元素,每次都是 O(n).而链式存储只有在第一次时是 O(n),其它是O(1)。
5、单链表的整表创建
在前面,我整理了一些链表的基本操作,但是呢,巧妇难为无米之炊,没有链表,你执行个什么操作啊?所以,本小节聊聊创建单链表。
对于顺序存储,其实就是一个数组的初始化,不赘述。
对于链式存储,创建一个单链表,实际上就是动态生成链表的过程,即从“空表”开始,依次建立各元素结点,并逐个插入到链表中。算法思路可以这样描述:
(1)声明一个结点 p 和计数器 i;
(2)初始化一个空链表(详见代码);
(3)让 L 的头结点的指针指向 NULL,即建立一个带头结点的单链表;
(4)进行循环:新生成一个结点,赋值给 p;随机生成一个数字(自己定义也可以),赋值给p的数据域 p->data;将 p 插入到头结点与前一新结点之间。
插入的方法,一般由头插法和尾插法。
5.1 头插法
头插入的思路是始终让新结点放在第一的位置。如图所示,结点 p 为新结点。
代码如下:
/* 随机产生n个元素的值,建立带表头结点的单链线性表L(头插法) */
void CreateListHead(LinkList *L, int n)
{
LinkList p;
int i;
srand(time(0)); /* 初始化随机数种子 */
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL; /* 先建立一个带头结点的单链表 */
for (i = 0; idata = rand() % 100 + 1; /* 随机生成100以内的数字 */
p->next = (*L)->next;
(*L)->next = p; /* 插入到表头 */
}
} 5.2 尾插法
循环结束后,应该让这个链表的指针域置空,因此,要执行 r->next = NULL; 目的是为了,在以后的遍历中,可以确认其为尾部。
代码如下:
/* 随机产生n个元素的值,建立带表头结点的单链线性表L(尾插法) */
void CreateListTail(LinkList *L, int n)
{
LinkList p, r;
int i;
srand(time(0)); /* 初始化随机数种子 */
*L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */
r = *L; /* r为指向尾部的结点 */
for (i = 0; idata = rand() % 100 + 1; /* 随机生成100以内的数字 */
r->next = p; /* 将表尾终端结点的指针指向新结点 */
r = p; /* 将当前的新结点定义为表尾终端结点 */
}
r->next = NULL; /* 表示当前链表结束 */
} 6、单链表的整表删除
当不再使用这个单链表时,我们需要把它销毁,也就是在内存中把所有的结点释放掉。具体思路为:
(1)声明两个结点 p 和 q;
(2)将第一个结点赋值给 p;
(3)循环: 将下一个结点赋值给q ; 释放 p ;将 q 赋值给 p;
在这里说一下,为什么要设置两个结点 p 和 q 呢?直接 free(p);p = p->next;不就行了吗?显然是不行的,因为 p 是一个结点,除了含有数据域外,还有指针域。删除了 p 结点后,指针域也不存在了,那么,p 的下一个结点 p->next 也就找不到了。
实现代码如下:
/* 初始条件:顺序线性表L已存在。操作结果:将L重置为空表 */
Status ClearList(LinkList *L)
{
LinkList p, q;
p = (*L)->next; /* p指向第一个结点 */
while (p) /* 没到表尾 */
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL; /* 头结点指针域为空 */
return OK;
}完整代码:
#include "stdio.h"
#include "string.h"
#include "ctype.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType;/* ElemType类型根据实际情况而定,这里假设为int */
Status visit(ElemType c)
{
printf("%d ", c);
return OK;
}
typedef struct Node
{
ElemType data;
struct Node *next;
}*LinkList;
//typedef struct Node *LinkList; /* 定义LinkList */
/* 初始化顺序线性表 */
Status InitList(LinkList *L)
{
*L = (LinkList)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */
if (!(*L)) /* 存储分配失败 */
return ERROR;
(*L)->next = NULL; /* 指针域为空 */ //也就是第一个结点为空
return OK;
}
/* 初始条件:顺序线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */
Status ListEmpty(LinkList L)
{
if (L->next)
return FALSE;
else
return TRUE;
}
/* 初始条件:顺序线性表L已存在。操作结果:将L重置为空表 */
Status ClearList(LinkList *L)
{
LinkList p, q;
p = (*L)->next; /* p指向第一个结点 */
while (p) /* 没到表尾 */
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL; /* 头结点指针域为空 */
return OK;
}
/* 初始条件:顺序线性表L已存在。操作结果:返回L中数据元素个数 */
int ListLength(LinkList L)
{
int i = 0;
LinkList p = L->next; /* p指向第一个结点 */
while (p)
{
i++;
p = p->next;
}
return i;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:用e返回L中第i个数据元素的值 */
Status GetElem(LinkList L, int i, ElemType *e)
{
int j;
LinkList p; /* 声明一结点p */
p = L->next; /* 让p指向链表L的第一个结点 */
j = 1; /* j为计数器 */
while (p && jnext; /* 让p指向下一个结点 */
++j;
}
if (!p || j>i)
return ERROR; /* 第i个元素不存在 */
*e = p->data; /* 取第i个元素的数据 */
return OK;
}
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 */
/* 若这样的数据元素不存在,则返回值为0 */
int LocateElem(LinkList L, ElemType e)
{
int i = 0;
LinkList p = L->next;
while (p)
{
i++;
if (p->data == e) /* 找到这样的数据元素 */
return i;
p = p->next;
}
return 0;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
int j;
LinkList p, s;
p = *L;
j = 1;
while (p && j < i) /* 寻找第i个结点 */
{
p = p->next;
++j;
}
if (!p || j > i)
return ERROR; /* 第i个元素不存在 */
s = (LinkList)malloc(sizeof(Node)); /* 生成新结点(C语言标准函数) */
s->data = e;
s->next = p->next; /* 将p的后继结点赋值给s的后继 */
p->next = s; /* 将s赋值给p的后继 */
return OK;
}
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */
Status ListDelete(LinkList *L, int i, ElemType *e)
{
int j;
LinkList p, q;
p = *L;
j = 1;
while (p->next && j < i) /* 遍历寻找第i个元素 */
{
p = p->next;
++j;
}
if (!(p->next) || j > i)
return ERROR; /* 第i个元素不存在 */
q = p->next;
p->next = q->next; /* 将q的后继赋值给p的后继 */
*e = q->data; /* 将q结点中的数据给e */
free(q); /* 让系统回收此结点,释放内存 */
return OK;
}
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:依次对L的每个数据元素输出 */
Status ListTraverse(LinkList L)
{
LinkList p = L->next;
while (p)
{
visit(p->data);
p = p->next;
}
printf("\n");
return OK;
}
/* 随机产生n个元素的值,建立带表头结点的单链线性表L(头插法) */
void CreateListHead(LinkList *L, int n)
{
LinkList p;
int i;
srand(time(0)); /* 初始化随机数种子 */
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL; /* 先建立一个带头结点的单链表 */
for (i = 0; idata = rand() % 100 + 1; /* 随机生成100以内的数字 */
p->next = (*L)->next;
(*L)->next = p; /* 插入到表头 */
}
}
/* 随机产生n个元素的值,建立带表头结点的单链线性表L(尾插法) */
void CreateListTail(LinkList *L, int n)
{
LinkList p, r;
int i;
srand(time(0)); /* 初始化随机数种子 */
*L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */
r = *L; /* r为指向尾部的结点 */
for (i = 0; idata = rand() % 100 + 1; /* 随机生成100以内的数字 */
r->next = p; /* 将表尾终端结点的指针指向新结点 */
r = p; /* 将当前的新结点定义为表尾终端结点 */
}
r->next = NULL; /* 表示当前链表结束 */
}
int main()
{
LinkList L;
ElemType e;
Status i;
int j, k;
i = InitList(&L);
printf("初始化L后:ListLength(L)=%d\n", ListLength(L));
for (j = 1; j <= 5; j++)
i = ListInsert(&L, 1, j);
printf("在L的表头依次插入1~5后:L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n", ListLength(L));
i = ListEmpty(L);
printf("L是否空:i=%d(1:是 0:否)\n", i);
i = ClearList(&L);
printf("清空L后:ListLength(L)=%d\n", ListLength(L));
i = ListEmpty(L);
printf("L是否空:i=%d(1:是 0:否)\n", i);
for (j = 1; j <= 10; j++)
ListInsert(&L, j, j);
printf("在L的表尾依次插入1~10后:L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n", ListLength(L));
ListInsert(&L, 1, 0);
printf("在L的表头插入0后:L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n", ListLength(L));
GetElem(L, 5, &e);
printf("第5个元素的值为:%d\n", e);
for (j = 3; j <= 4; j++)
{
k = LocateElem(L, j);
if (k)
printf("第%d个元素的值为%d\n", k, j);
else
printf("没有值为%d的元素\n", j);
}
k = ListLength(L); /* k为表长 */
for (j = k + 1; j >= k; j--)
{
i = ListDelete(&L, j, &e); /* 删除第j个数据 */
if (i == ERROR)
printf("删除第%d个数据失败\n", j);
else
printf("删除第%d个的元素值为:%d\n", j, e);
}
printf("依次输出L的元素:");
ListTraverse(L);
j = 5;
ListDelete(&L, j, &e); /* 删除第5个数据 */
printf("删除第%d个的元素值为:%d\n", j, e);
printf("依次输出L的元素:");
ListTraverse(L);
i = ClearList(&L);
printf("\n清空L后:ListLength(L)=%d\n", ListLength(L));
CreateListHead(&L, 20);
printf("整体创建L的元素(头插法):");
ListTraverse(L);
i = ClearList(&L);
printf("\n删除L后:ListLength(L)=%d\n", ListLength(L));
CreateListTail(&L, 20);
printf("整体创建L的元素(尾插法):");
ListTraverse(L);
return 0;
} 7、单链表与顺序存储优缺点对比
存储分配方式:顺序存储用一段连续的存储单元依次存储线性表的数据元素;单链表是用一组任意的存储单元存放数据元素。
查找时间性能:顺序存储 O(1); 单链表 O(n);
插入和删除时间性能:顺序存储需要平均移动表长一半的元素,时间为 O(n);单链表一旦查找到某位置的指针后,插入和删除仅为 O(1).
空间性能:顺序存储需要预分配存储空间,分配多了,浪费内存,分配少了容易上溢;单链表可以实现动态分配,元素个数不受限制。
总结:
(1)如果线性表需要频繁查找,很少进行插入和删除,适宜采用顺序存储结构。如果频繁插入和删除,适宜采用单链表结构。比如在游戏开发中,对于用户注册的个人信息,除了注册时候的插入数据意外,绝大多数都是读取,所以,最好采用顺序存储结构。而游戏中玩家的武器装备等,在游戏的过程中,可能随时增加或者删除,适宜最好采用单链表结构;
(2)如果线性表元素个数变化很大,或者预先我们不知道线性表的长度有多大,最好采用单链表结构,如此一来,就不需要考虑空间存储的问题。如果呢,我们事先知道线性表的大致长度,比如一年有12个月,一周有七天,那么肯定采用顺序存储结构,因为效率会更高一些。