脊回归（Ridge Regression）详解

    脊回归（Ridge Regression）

    转载于：http://blog.csdn.net/daunxx/article/details/51578787

    在《线性回归（Linear Regression）》中提到过，当使用最小二乘法计算线性回归模型参数的时候，如果数据集合矩阵（也叫做设计矩阵(design matrix)）X，存在多重共线性，那么最小二乘法对输入变量中的噪声非常的敏感，其解会极为不稳定。为了解决这个问题，就有了这一节脊回归（Ridge Regression ）。

    当设计矩阵X存在多重共线性的时候（数学上称为病态矩阵
多重共线性（Multicollinearity）是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。一般来说，由于经济数据的限制使得模型设计不当，导致设计矩阵中解释变量间存在普遍的相关关系。完全共线性的情况并不多见，一般出现的是在一定程度上的共线性，即近似共线性。），最小二乘法求得的参数w在数值上会非常的大，而一般的线性回归其模型是y=wTx ，显然，就是因为w在数值上非常的大，所以，如果输入变量x有一个微小的变动，其反应在输出结果上也会变得非常大，这就是对输入变量总的噪声非常敏感的原因。

    如果能限制参数w的增长，使w不会变得特别大，那么模型对输入w中噪声的敏感度就会降低。这就是脊回归和套索回归（Ridge Regression and Lasso Regrission）的基本思想。

    为了限制模型参数w的数值大小，就在模型原来的目标函数上加上一个惩罚项（即正则化项），这个过程叫做正则化（Regularization）。

如果惩罚项是参数的l2范数，就是脊回归(Ridge Regression)

如果惩罚项是参数的l1范数，就是套索回归（Lasso Regrission）

正则化同时也是防止过拟合有效的手段，这在“多项式回归”中有详细的说明。

脊回归(Ridge Regression)

    所谓脊回归，就是对于一个线性模型，在原来的损失函数加入参数的l2范数的惩罚项，其损失函数为如下形式:

Jw=minw{||Xw−y||2+α||w||2}

    这里α是平法损失和正则项之间的一个系数，α≥0。

α的数值越大，那么正则项，也是惩罚项的作用就越明显；α的数值越小，正则项的作用就越弱。极端情况下，α=0则和原来的损失函数是一样的，如果α=∞，则损失函数只有正则项，此时其最小化的结果必然是w=0。

关于alpha的数值具体的选择，归于“模型选择”章节，具体的方法可以参见“模型选择”。

其实，这个式子和拉格朗日乘子法的结果差不多，如果逆用拉格朗日乘子法的话，那么，上面的损失函数可以是下面的这种优化模型：

Jw=minw{||Xw−y||2}||w||2≤t

在《线性回归》中，给出了线性回归的损失函数可以写为：

∥Xw−y∥2=(Xw−y)T(Xw−y)

关于参数w求导之后：

XT(Xw−y)+XT(Xw−y)=0

其解为：

w=(XTX)−1XTy

这里，脊回归的损失函数为：

∥Xw−y∥2+α||w||2=(Xw−y)T(Xw−y)+αwTw

关于参数w求导之后：

XT(Xw−y)+XT(Xw−y)+αw=0

其解为：

w=(XTX+αI)−1XTy

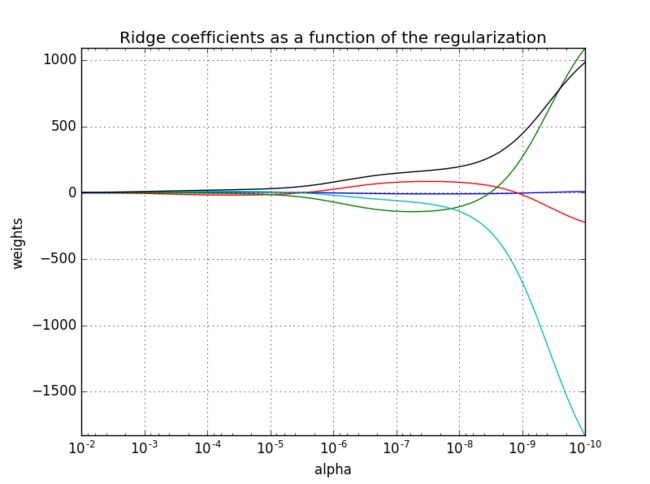
    下面给出一个脊回归简单的代码示例，这个代码显示了不同的alpha对模型参数w的影响程度。alpha越大，则w的数值上越小；alpha越小，则w的数值上越大，注意所生成的图片为了更好的观察，将x轴做了反转。

#!/usr/bin/python
# -*- coding: utf-8 -*-

"""
author ： [email protected]
time : 2016-06-03-14-34

脊回归测试代码
这里需要先生成一个线性相关的设计矩阵X，再使用脊回归对其进行建模
脊回归中最重要的就是参数alpha的选择，本例显示了不同的alpha下
模型参数omega不同的结果

"""

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# 这里设计矩阵X是一个希尔伯特矩阵（Hilbert matrix）
# 其元素A（i,j）=1(i + j -1),i和j分别为其行标和列标
# 希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态
# 即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化
# 这里设计矩阵是一个10x5的矩阵，即有10个样本，5个变量
X = 1. / (np.arange(1, 6) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

print '设计矩阵为：'
print X

# alpha 取值为10^（-10）到10^（-2）之间的连续的200个值
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
print '\n alpha的值为：'
print alphas

# 初始化一个Ridge Regression
clf = linear_model.Ridge(fit_intercept=False)

# 参数矩阵，即每一个alpha对于的参数所组成的矩阵
coefs = []
# 根据不同的alpha训练出不同的模型参数
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(X, y)
    coefs.append(clf.coef_)

# 获得绘图句柄
ax = plt.gca()
# 参数中每一个维度使用一个颜色表示
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k'])

# 绘制alpha和对应的参数之间的关系图
ax.plot(alphas, coefs)
ax.set_xscale('log')    #x轴使用对数表示
ax.set_xlim(ax.get_xlim()[::-1])  # 将x轴反转，便于显示
plt.grid()
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63

基于交叉验证的脊回归

在前面提到过，脊回归中，alpha的选择是一个比较麻烦的问题，这其实是一个模型选择的问题，在模型选择中，最简单的模型选择方法就是交叉验证（Cross-validation），将交叉验证内置在脊回归中，就免去了alpha的人工选择，其具体实现方式如下：

#!/usr/bin/python
# -*- coding: utf-8 -*-

"""
author ： [email protected]
time : 2016-06-19-20-59

基于交叉验证的脊回归alpha选择
可以直接获得一个相对不错的alpha

"""


print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model


# 这里设计矩阵X是一个希尔伯特矩阵（Hilbert matrix）
# 其元素A（i,j）=1(i + j -1),i和j分别为其行标和列标
# 希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态
# 即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化
# 这里设计矩阵是一个10x5的矩阵，即有10个样本，5个变量
X = 1. / (np.arange(1, 6) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

print '设计矩阵为：'
print X

# 初始化一个Ridge Cross-Validation Regression
clf = linear_model.RidgeCV(fit_intercept=False)

# 训练模型
clf.fit(X, y)

print
print 'alpha的数值 : ', clf.alpha_
print '参数的数值：', clf.coef_

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41

其运行结果如下：

设计矩阵为：
[[ 1.          0.5         0.33333333  0.25        0.2       ]
 [ 0.5         0.33333333  0.25        0.2         0.16666667]
 [ 0.33333333  0.25        0.2         0.16666667  0.14285714]
 [ 0.25        0.2         0.16666667  0.14285714  0.125     ]
 [ 0.2         0.16666667  0.14285714  0.125       0.11111111]
 [ 0.16666667  0.14285714  0.125       0.11111111  0.1       ]
 [ 0.14285714  0.125       0.11111111  0.1         0.09090909]
 [ 0.125       0.11111111  0.1         0.09090909  0.08333333]
 [ 0.11111111  0.1         0.09090909  0.08333333  0.07692308]
 [ 0.1         0.09090909  0.08333333  0.07692308  0.07142857]]

alpha的数值 :  0.1
参数的数值： [-0.43816548  1.19229228  1.54118834  1.60855632  1.58565451]