Direct3D基础--渲染管线

本文为 Introduction to 3D Game Programming with DirectX 11 读书笔记

Color的XNA实现

XMVECTOR XMLoadColor(CONST XMCOLOR* pSource);

VOID XMStoreColor(XMCOLOR* pDestination, FXMVECTOR V);

Rendering Pipline

Input Assembler stage

input assembler (IA) 阶段从内存中读取几何数据，然后用它组合成几何原型（三角形、线等）。

Primitive Topology

被传输到渲染管线的顶点集合称为 vertex buffer，通过指定 primitive topology 来告诉Direct3D怎么从vertex数据中构成集合基元。

void ID3D11DeviceContext::IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY Topology);

typedef enum D3D11_PRIMITIVE_TOPOLOGY
{
    D3D11_PRIMITIVE_TOPOLOGY_UNDEFINED = 0,
    D3D11_PRIMITIVE_TOPOLOGY_POINTLIST = 1,
    D3D11_PRIMITIVE_TOPOLOGY_LINELIST = 2,
    D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP = 3,
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST = 4,
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP = 5,
    D3D11_PRIMITIVE_TOPOLOGY_LINELIST_ADJ = 10,
    D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP_ADJ = 11,
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST_ADJ = 12,
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP_ADJ = 13,
    D3D11_PRIMITIVE_TOPOLOGY_1_CONTROL_POINT_PATCHLIST = 33,
    D3D11_PRIMITIVE_TOPOLOGY_2_CONTROL_POINT_PATCHLIST = 34,
    ...
    D3D11_PRIMITIVE_TOPOLOGY_32_CONTROL_POINT_PATCHLIST = 64,
} D3D11_PRIMITIVE_TOPOLOGY;

例子：

md3dImmediateContext->IASetPrimitiveTopology(
    D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP);
/* ...draw objects using triangle strip... */

选择各种primitive_topology形成的基元

上图的图b表示带邻接三角形的三角形列表，adjacent triangles的表示也必须在输入中提供

Indices

因为直接重复的给顶点数据的话，顶点会有很大的冗余，所以使用Index来构成primitive。
例如：

Vertex v [9] = {v0, v1, v2, v3, v4, v5, v6, v7, v8};

UINT indexList[24] = {
    0, 1, 2, // Triangle 0
    0, 2, 3, // Triangle 1
    0, 3, 4, // Triangle 2
    0, 4, 5, // Triangle 3
    0, 5, 6, // Triangle 4
    0, 6, 7, // Triangle 5
    0, 7, 8, // Triangle 6
    0, 8, 1 // Triangle 7
};

The vertex shader stage

顶点着色器对顶点数据进行处理。

• 把对象从local坐标系转换到world坐标系
• 把world坐标系转换到camera坐标系（又称view space, eye space, or camera space），得到

在介绍View Space的时候，书上是先介绍的camera的坐标相对于world坐标的偏移，从view space到world space的转换矩阵 W，其中 W=RT W = R T ，那么world space到view space的转换矩阵就是

V=⎡⎣⎢⎢⎢⎢uxvxwxQxuyvywyQyuzvzwzQz0001⎤⎦⎥⎥⎥⎥ V = [ u x u y u z 0 v x v y v z 0 w x w y w z 0 Q x Q y Q z 1 ]

V=W−1=(RT)−1=T−1R−1=T−1RT=⎡⎣⎢⎢⎢⎢100−Qx010−Qy001−Qz0001⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢uxuyuz0vxvyvz0wxwywz00001⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢uxuyuz−Qxvxvyvz−Qywxwywz−Qz0001⎤⎦⎥⎥⎥⎥ V = W − 1 = ( R T ) − 1 = T − 1 R − 1 = T − 1 R T = [ 1 0 0 0 0 1 0 0 0 0 1 0 − Q x − Q y − Q z 1 ] [ u x v x w x 0 u y v y w y 0 u z v z w z 0 0 0 0 1 ] = [ u x v x w x 0 u y v y w y 0 u z v z w z 0 − Q x − Q y − Q z 1 ]

对Unity的shader比较熟悉的朋友可能会看到
#define COMPUTE_EYEDEPTH(o) o = -UnityObjectToViewPos( v.vertex ).z
这里取出z后在前面加了一个负号，这个还没有特别好的解释，关于这个计算

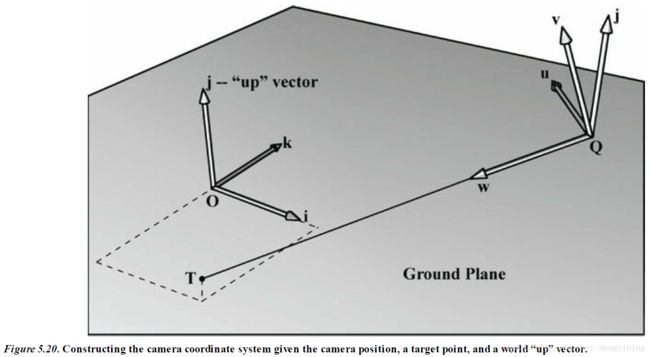
给定camera的坐标，构造camera坐标系统，因为world space的轴现在是作为标准的坐标，所以这里求出来的就是view space相对于world space的转换，再把上面说的 V=W−1 V = W − 1 考虑一下，就可以得到world space到view space的转矩阵了。 j=(0,1,0) j = ( 0 , 1 , 0 )

w=T−Q||T−Q||u=j×w||j×w||v=w×u w = T − Q | | T − Q | | u = j × w | | j × w | | v = w × u

XNA也提供了函数实现

XMMATRIX XMMatrixLookAtLH( // Outputs resulting view matrix V
    FXMVECTOR EyePosition, // Input camera position Q
    FXMVECTOR FocusPosition, // Input target point T
    FXMVECTOR UpDirection); // Input world up vector j

例子：

XMVECTOR pos = XMVectorSet(5, 3, -10, 1.0f);
XMVECTOR target = XMVectorZero();
XMVECTOR up = XMVectorSet(0.0f, 1.0f, 0.0f, 0.0f);
XMMATRIX V = XMMatrixLookAtLH(pos, target, up);

Projection and Homogeneous Clip Space

齐次坐标

给定欧式平面上一点(x,y)，对任意非零实数z，三元组(xZ,yZ,Z)即称之为该点的齐次坐标。与笛卡尔坐标不同，一个点可以有无限多个齐次坐标表示法。
- 当Z不为0，则表示欧氏平面上该点为(X/Z,Y/Z)
- 当Z为0，则该点表示一无穷远点
三元组(0,0,0)不表示任何点，原点表示为(0,0,1)。

Defining a Frustum

定义视椎体的4个数：近平面 n n ，远平面 f f ，竖直视角(vertical field of view angle) α α ，aspect ratio r r .
aspect ratio : r=w/h r = w / h ，其中w和h分别为投影窗口的宽和高。

r=wh=w2⇒w=2rtan(α2)=1d⇒d=cot(α2)tan(β2)=rd=rcot(α2)=r⋅tan(α2)horzontal field of view angle ββ=2tan−1(r⋅tan(α2)) r = w h = w 2 ⇒ w = 2 r tan ⁡ ( α 2 ) = 1 d ⇒ d = cot ⁡ ( α 2 ) tan ⁡ ( β 2 ) = r d = r cot ⁡ ( α 2 ) = r ⋅ tan ⁡ ( α 2 ) horzontal field of view angle  β β = 2 tan − 1 ⁡ ( r ⋅ tan ⁡ ( α 2 ) )

Projecting Vertices

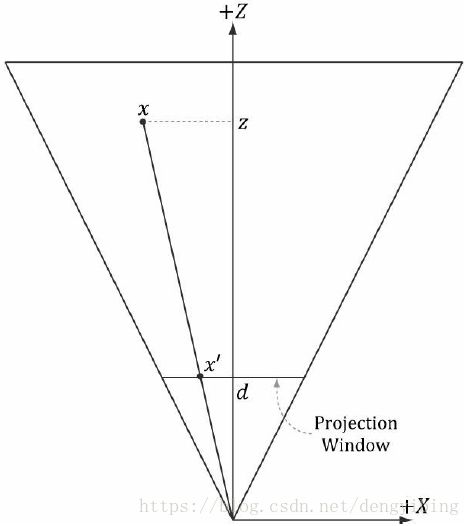
给定视椎体中一个顶点 (x,y,z) ( x , y , z ) ，投影到近平面上 (x′,y′,d) ( x ′ , y ′ , d )
公式如下：

x′d=xz⇒x′=xdz=xcot(α/2)z=xztan(α/2)y′d=yz⇒y′=ydz=ycot(α/2)z=yztan(α/2) x ′ d = x z ⇒ x ′ = x d z = x cot ⁡ ( α / 2 ) z = x z tan ⁡ ( α / 2 ) y ′ d = y z ⇒ y ′ = y d z = y cot ⁡ ( α / 2 ) z = y z tan ⁡ ( α / 2 )

如果一个点在视椎体中，那么就有：

−r≤x′≤r−1≤y′≤1n≤z≤f − r ≤ x ′ ≤ r − 1 ≤ y ′ ≤ 1 n ≤ z ≤ f

标准设备空间 Normalized Device Coordinates (NDC)

为什么需要标准设备空间，因为从视椎体近平面和camera的设置有关，屏幕空间和硬件屏幕有关，这两者之间需要一个桥梁来做转换，所以NDC非常有必要。

在NDC中只有满足如下条件，一个点在camera space才处于视椎体中（下面的z还没有标准化）

−1≤x′/r≤1−1≤y′≤1n≤z≤f − 1 ≤ x ′ / r ≤ 1 − 1 ≤ y ′ ≤ 1 n ≤ z ≤ f

修改投影公式，使之直接将点映射到NDC

x′=xrztan(α/2)y′=yztan(α/2) x ′ = x r z tan ⁡ ( α / 2 ) y ′ = y z tan ⁡ ( α / 2 )

把投影等式写成矩阵形式

这里用了一个小trick，将过程分解为线性和非线性的两个部分。非线性部分就是最后除以z

则投影矩阵为，假设 A,B A , B 为常数

P=⎡⎣⎢⎢⎢⎢⎢1rtan(α/2)00001tan(α/2)0000AB0010⎤⎦⎥⎥⎥⎥⎥ P = [ 1 r tan ⁡ ( α / 2 ) 0 0 0 0 1 tan ⁡ ( α / 2 ) 0 0 0 0 A 1 0 0 B 0 ]

则对任意顶点 (x,y,z,1) ( x , y , z , 1 )

[x,y,z,1]⎡⎣⎢⎢⎢⎢⎢1rtan(α/2)00001tan(α/2)0000AB0010⎤⎦⎥⎥⎥⎥⎥=[xrtan(α/2),ytan(α/2),Az+B,z] [ x , y , z , 1 ] [ 1 r tan ⁡ ( α / 2 ) 0 0 0 0 1 tan ⁡ ( α / 2 ) 0 0 0 0 A 1 0 0 B 0 ] = [ x r tan ⁡ ( α / 2 ) , y tan ⁡ ( α / 2 ) , A z + B , z ]

做完投影的线性变换之后，除以w维， w=z w = z 。这就是非线性部分

[xrtan(α/2),ytan(α/2),Az+B,z]→divide by w[xrztan(α/2),yztan(α/2),A+Bz,1] [ x r tan ⁡ ( α / 2 ) , y tan ⁡ ( α / 2 ) , A z + B , z ] → divide by w [ x r z tan ⁡ ( α / 2 ) , y z tan ⁡ ( α / 2 ) , A + B z , 1 ]

除以 w w 有是被称为 perspective divide或者 homogeneous divide

标准化深度值

上面假设了A和B为常数，最后要将深度值从 [n,f] [ n , f ] 映射到 [0,1] [ 0 , 1 ] 上。
令 g(z)=A+Bz g ( z ) = A + B z ，则必须满足 g(n)=0,g(f)=1 g ( n ) = 0 , g ( f ) = 1
则

A=ff−nB=−nff−n A = f f − n B = − n f f − n

最终得到的正交投影矩阵(perspective projection matrix)为

P=⎡⎣⎢⎢⎢⎢⎢⎢⎢1rtan(α/2)00001tan(α/2)0000ff−n−nff−n0010⎤⎦⎥⎥⎥⎥⎥⎥⎥ P = [ 1 r tan ⁡ ( α / 2 ) 0 0 0 0 1 tan ⁡ ( α / 2 ) 0 0 0 0 f f − n 1 0 0 − n f f − n 0 ]

XMMatrixPerspectiveFovLH

该投影矩阵也被XNA实现了

XMMATRIX XMMatrixPerspectiveFovLH( // returns projection matrix
    FLOAT FovAngleY, // vertical field of view angle in radians
    FLOAT AspectRatio, // aspect ratio = width / height
    FLOAT NearZ, // distance to near plane
    FLOAT FarZ); // distance to far plane

例子：

XMMATRIX P = XMMatrixPerspectiveFovLH(0.25f*MathX::Pi,
    AspectRatio(), 1.0f, 1000.0f);

//The aspect ratio is taken to match our window aspect ratio:
float D3DApp::AspectRatio()const
{
    return static_cast<float>(mClientWidth) / mClientHeight;
}

THE TESSELLATION STAGES

Tessellation是指把mesh的三角形再分割，添加新的三角形

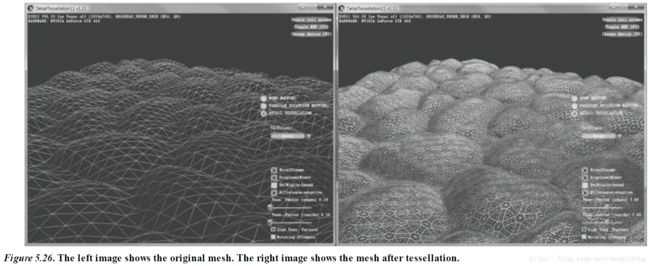
THE GEOMETRY SHADER STAGE

geometry shader是可选的，它的主要优势是可以create or destroy geometry

剪裁 CLIPPING

将对象处在视椎体之外的部分剪裁掉


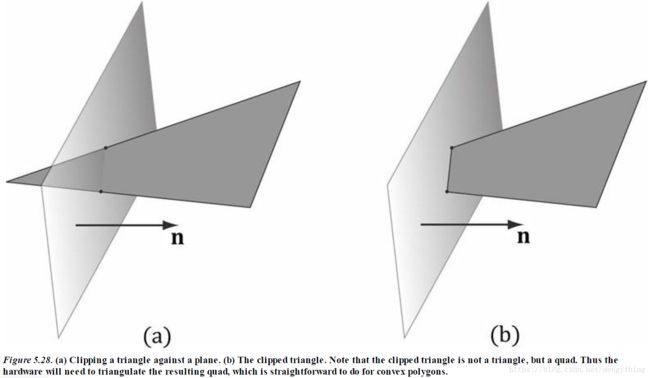
在homogeneous clip space中，在除以w之前，4D坐标为 (x,y,z,w) ( x , y , z , w ) ，则

−w≤x≤w−w≤y≤w0≤z≤w − w ≤ x ≤ w − w ≤ y ≤ w 0 ≤ z ≤ w

THE RASTERIZATION STAGE(光栅化)

光栅化阶段主要是，从投影的3D三角形，计算pixel color

视口转换（Viewport Transform）

从NDC转换到真实的要输出的窗口或者屏幕坐标

背面剪裁（Backface Culling）

背面剪裁是指将背对着camera的三角形剪裁掉
判断是否背对着camera

e0=v1−v0e1=v2−v1n=e0×e1||e0×e1|| e 0 = v 1 − v 0 e 1 = v 2 − v 1 n = e 0 × e 1 | | e 0 × e 1 | |

法向量对着camera的是正面front face，否则就是back face

Vertex Attribute Interpolation

必须对3D space的顶点的深度值，纹理采样点等信息做差值，这需要 perspective correct interpolation，并不是线性差值，如果直接线性差值将会得到下面演示的错误情况。

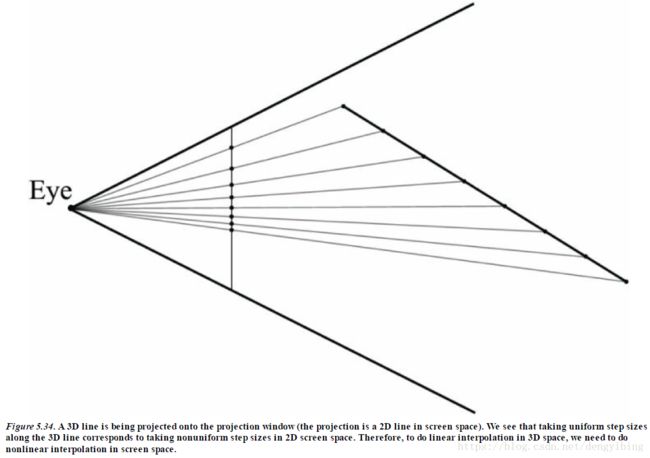
下图就是对深度值错误的差值

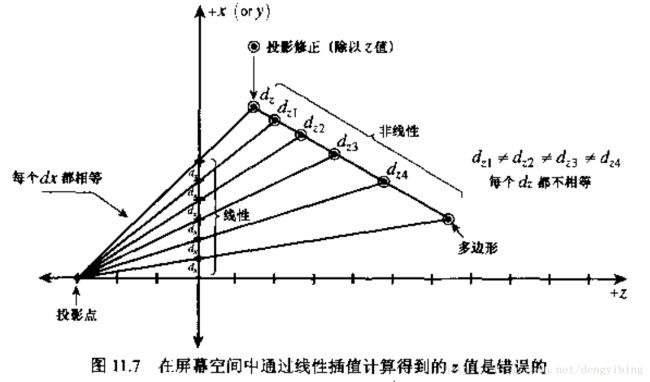
上图中多边形中screen space各线性差值点对应的world space的z不是线性变化的，而1/z是线性变化的。

THE PIXEL SHADER STAGE

逐像素的计算最后输出的值，这里可以做跟颜色阴影相关的计算

THE OUTPUT MERGER STAGE

所有没有被reject的输出都要写到back buffer。Blending就是在这个阶段做的。

---

补充:透视纹理修正和1/z缓存

参考自《3D游戏编程大师技巧》

z在屏幕空间中不呈线性变化，只有1/z才呈线性变化。

证明：
使用下述两点之间的差值公式：

p=(1−t)∗p1+(t)∗p2(1) (1) p = ( 1 − t ) ∗ p 1 + ( t ) ∗ p 2

其中p可以是向量，也可以是标量。
由下图推导出关系

在上图中，有两个位于世界坐标空间中的点，他们的坐标分别是 (y1,z1) ( y 1 , z 1 ) 和 (y2,z2) ( y 2 , z 2 ) 。将这些点投影到 z=d z = d 的视平面上，得到点 (p1,d) ( p 1 , d ) 和 (p2,d) ( p 2 , d ) 。另外，线段上任意一点 (y,z) ( y , z ) 投影到视平面上时得到点 (p,d) ( p , d ) 。

在3D空间中，位于y-z平面中（x=0）的直线的方程为：

a∗y+b∗z=c a ∗ y + b ∗ z = c

看上图，根据三角形相似可知，焦点 (p,d) ( p , d ) 和3D点 (y,z) ( y , z ) 是相似三角形上对应的点：
p/y=d/z p / y = d / z
求解y，得到
y=(p/d)∗z y = ( p / d ) ∗ z ，
带入到直线方程，得到
(a∗p/d)∗z+b∗z=c ( a ∗ p / d ) ∗ z + b ∗ z = c ，
将等式两边除以 (a∗p/d) ( a ∗ p / d ) ，得到
z=c/((a∗p/d)+b) z = c / ( ( a ∗ p / d ) + b ) ，
等式两边取倒数，得到
1/z=((a∗p/d)+b)/c=(a∗p/c∗d)+(b/c) 1 / z = ( ( a ∗ p / d ) + b ) / c = ( a ∗ p / c ∗ d ) + ( b / c ) ，
将变量p与其他常量分离，得到

1/z=(a/c∗d)∗p+(b/c)(2) (2) 1 / z = ( a / c ∗ d ) ∗ p + ( b / c )

将上述两个点以及其投影点带入上述等式，得到

1/z1=(a/c∗d)∗p1+(b/c)1/z2=(a/c∗d)∗p2+(b/c) 1 / z 1 = ( a / c ∗ d ) ∗ p 1 + ( b / c ) 1 / z 2 = ( a / c ∗ d ) ∗ p 2 + ( b / c )

再带入到最上提到的差值公式（1），得到
1/z=(a/c∗d)[(1−t)∗p1+(t)∗p2]+(b/c) 1 / z = ( a / c ∗ d ) [ ( 1 − t ) ∗ p 1 + ( t ) ∗ p 2 ] + ( b / c )
做一下变换，得到

1/z=[(a/c∗d)∗p1+(b/c)]∗(1−t)+[(a/c∗d)∗p2+(b/c)]∗(t)(3) (3) 1 / z = [ ( a / c ∗ d ) ∗ p 1 + ( b / c ) ] ∗ ( 1 − t ) + [ ( a / c ∗ d ) ∗ p 2 + ( b / c ) ] ∗ ( t )

观察等式（2）与等式（3）的关系，使用 1/z1 1 / z 1 替换右边的项，可以得到

1/z=[(1/z1)]∗(1−t)+[(1/z2)]∗(t) 1 / z = [ ( 1 / z 1 ) ] ∗ ( 1 − t ) + [ ( 1 / z 2 ) ] ∗ ( t )

这意味着可以在 1/z1 1 / z 1 和 1/z2 1 / z 2 之间进行线性差值。换句话说，任何3D空间量除以z的商在屏幕空间中都是呈线性变化的。