动态规划--数字三角形，最长上升子序列，最长公共子序列

本文部分内容转载自https://blog.csdn.net/baidu_28312631/article/details/47418773

    动态规划相信大家都知道，动态规划算法也是新手在刚接触算法设计时很苦恼的问题，有时候觉得难以理解，但是真正理解之后，就会觉得动态规划其实并没有想象中那么难。网上也有很多关于讲解动态规划的文章，大多都是叙述概念，讲解原理，让人觉得晦涩难懂，即使一时间看懂了，发现当自己做题的时候又会觉得无所适从。我觉得，理解算法最重要的还是在于练习，只有通过自己练习，才可以更快地提升。话不多说，接下来，下面我就通过一个例子来一步一步讲解动态规划是怎样使用的，只有知道怎样使用，才能更好地理解，而不是一味地对概念和原理进行反复琢磨。

    首先，我们看一下这道题（此题目来源于北大POJ）：

    数字三角形(POJ1163)

    

    在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。 三角形的行数大于1小于等于100，数字为 0 - 99

    输入格式：

    5      //表示三角形的行数    接下来输入三角形

    7

    3   8

    8   1   0

    2   7   4   4

    4   5   2   6   5

    要求输出最大和

    接下来，我们来分析一下解题思路：

    首先，肯定得用二维数组来存放数字三角形

    然后我们用D( r, j) 来表示第r行第 j 个数字(r,j从1开始算)

    我们用MaxSum(r, j)表示从D(r,j)到底边的各条路径中，最佳路径的数字之和。

    因此，此题的最终问题就变成了求 MaxSum(1,1)

    当我们看到这个题目的时候，首先想到的就是可以用简单的递归来解题：

    D(r, j)出发，下一步只能走D(r+1,j)或者D(r+1, j+1)。故对于N行的三角形，我们可以写出如下的递归式：   

if ( r == N)                
	MaxSum(r,j) = D(r,j)  
else      
	MaxSum( r, j) = Max{ MaxSum(r＋1,j), MaxSum(r+1,j+1) } + D(r,j) 

根据上面这个简单的递归式，我们就可以很轻松地写出完整的递归代码： 

#include   
#include  
#define MAX 101  
using namespace std; 
int D[MAX][MAX];  
int n;  
int MaxSum(int i, int j){    
	if(i==n)  
		return D[i][j];    
	int x = MaxSum(i+1,j);    
	int y = MaxSum(i+1,j+1);    
	return max(x,y)+D[i][j];  
}
int main(){    
	int i,j;    
	cin >> n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++)        
			cin >> D[i][j];    
	cout << MaxSum(1,1) << endl;  
}      

对于如上这段递归的代码，当我提交到POJ时，会显示如下结果：

   

    对的，代码运行超时了，为什么会超时呢？

    答案很简单，因为我们重复计算了，当我们在进行递归时，计算机帮我们计算的过程如下图（红色的数字为该数的计算次数）：

    

    就拿第三行数字1来说，当我们计算从第2行的数字3开始的MaxSum时会计算出从1开始的MaxSum，当我们计算从第二行的数字8开始的MaxSum的时候又会计算一次从1开始的MaxSum，也就是说有重复计算。这样就浪费了大量的时间。也就是说如果采用递规的方法，深度遍历每条路径，存在大量重复计算。则时间复杂度为 2的n次方,对于 n = 100 行，肯定超时。 

    接下来，我们就要考虑如何进行改进，我们自然而然就可以想到如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。那么可以用n方的时间复杂度完成计算。因为三角形的数字总数是 n(n+1)/2

    根据这个思路，我们就可以将上面的代码进行改进，使之成为记忆递归型的动态规划程序： 

#include   
#include  
using namespace std;
 
#define MAX 101
  
int D[MAX][MAX];    
int n;  
int maxSum[MAX][MAX];
 
int MaxSum(int i, int j){      
	if( maxSum[i][j] != -1 )         
		return maxSum[i][j];      
	if(i==n)   
		maxSum[i][j] = D[i][j];     
	else{    
		int x = MaxSum(i+1,j);       
		int y = MaxSum(i+1,j+1);       
		maxSum[i][j] = max(x,y)+ D[i][j];     
	}     
	return maxSum[i][j]; 
} 
int main(){    
	int i,j;    
	cin >> n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++) {       
			cin >> D[i][j];       
			maxSum[i][j] = -1;   
		}    
	cout << MaxSum(1,1) << endl; 
} 

当我们提交如上代码时，结果就是一次AC

    

    虽然在短时间内就AC了。但是，我们并不能满足于这样的代码，因为递归总是需要使用大量堆栈上的空间，很容易造成栈溢出，我们现在就要考虑如何把递归转换为递推，让我们一步一步来完成这个过程。

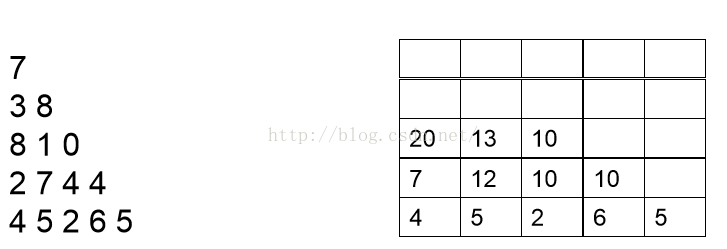
    我们首先需要计算的是最后一行，因此可以把最后一行直接写出，如下图：

    

    现在开始分析倒数第二行的每一个数，现分析数字2，2可以和最后一行4相加，也可以和最后一行的5相加，但是很显然和5相加要更大一点，结果为7，我们此时就可以将7保存起来，然后分析数字7，7可以和最后一行的5相加，也可以和最后一行的2相加，很显然和5相加更大，结果为12，因此我们将12保存起来。以此类推。。我们可以得到下面这张图：

    

    然后按同样的道理分析倒数第三行和倒数第四行，最后分析第一行，我们可以依次得到如下结果：

    

    

    上面的推导过程相信大家不难理解，理解之后我们就可以写出如下的递推型动态规划程序： 

#include   
#include  
using namespace std; 
 
#define MAX 101  
 
int D[MAX][MAX];   
int n;  
int maxSum[MAX][MAX]; 
int main(){    
	int i,j;    
	cin >> n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++)        
			cin >> D[i][j];   
	for( int i = 1;i <= n; ++ i )     
		maxSum[n][i] = D[n][i];   
	for( int i = n-1; i>= 1;  --i )     
		for( int j = 1; j <= i; ++j )         
			maxSum[i][j] = max(maxSum[i+1][j],maxSum[i+1][j+1]) + D[i][j];    
	cout << maxSum[1][1] << endl;  
} 

 

我们的代码仅仅是这样就够了吗？当然不是，我们仍然可以继续优化，而这个优化当然是对于空间进行优化，其实完全没必要用二维maxSum数组存储每一个MaxSum(r,j),只要从底层一行行向上递推，那么只要一维数组maxSum[100]即可,即只要存储一行的MaxSum值就可以。

     对于空间优化后的具体递推过程如下：

  

接下里的步骤就按上图的过程一步一步推导就可以了。进一步考虑，我们甚至可以连maxSum数组都可以不要，直接用D的第n行直接替代maxSum即可。但是这里需要强调的是：虽然节省空间，但是时间复杂度还是不变的。

    依照上面的方式，我们可以写出如下代码：    

#include   
#include  
using namespace std; 
 
#define MAX 101  
 
int D[MAX][MAX];  
int n; 
int * maxSum; 
 
int main(){    
	int i,j;    
	cin >> n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++)        
			cin >> D[i][j];   
	maxSum = D[n]; //maxSum指向第n行    
	for( int i = n-1; i>= 1;  --i )     
		for( int j = 1; j <= i; ++j )       
			maxSum[j] = max(maxSum[j],maxSum[j+1]) + D[i][j];    
	cout << maxSum[1] << endl;  
}

接下来，我们就进行一下总结：

    递归到动规的一般转化方法

    递归函数有n个参数，就定义一个n维的数组，数组的下标是递归函数参数的取值范围，数组元素的值是递归函数的返回值，这样就可以从边界值开始， 逐步填充数组，相当于计算递归函数值的逆过程。

    动规解题的一般思路

    1. 将原问题分解为子问题

    把原问题分解为若干个子问题，子问题和原问题形式相同或类似，只不过规模变小了。子问题都解决，原问题即解决(数字三角形例）。
    子问题的解一旦求出就会被保存，所以每个子问题只需求 解一次。
    2.确定状态

    在用动态规划解题时，我们往往将和子问题相关的各个变量的一组取值，称之为一个“状 态”。一个“状态”对应于一个或多个子问题， 所谓某个“状态”下的“值”，就是这个“状 态”所对应的子问题的解。

    一般经常碰到的情况是，K个整型变量能构成一个状态（如数字三角形中的行号和列号这两个变量构成一个“状态”）。如果这K个整型变量的取值范围分别是N1,N2,N3,...,Nk，那么，我们就可以用一个K维的数组array[N1][N2][N3]...[Nk]来存储各个状态的“值”。这个值未必就是一个整数或者浮点数，可能是需要一个结构才能表示的，那么array就可以是一个结构数组struct{}。一个“状态”下的“值”通常回事一个或多个子问题的解。
    所有“状态”的集合，构成问题的“状态空间”。“状态空间”的大小，与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里，一共有N×(N+1)/2个数字，所以这个问题的状态空间里一共就有N×(N+1)/2个状态。
    整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次，且在每个状态上作计算所花的时间都是和N无关的常数。

    3.确定一些初始状态（边界状态）的值

    以“数字三角形”为例，初始状态就是底边数字，值就是底边数字值。

    4. 确定状态转移方程

     定义出什么是“状态”，以及在该“状态”下的“值”后，就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”，求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示，此递推公式也可被称作“状态转移方程”。

    数字三角形的状态转移方程:

能用动规解决的问题的特点

    1) 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的，我们就称该问题具有最优子结 构性质。

    2) 无后效性。当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。

以上转载自https://blog.csdn.net/baidu_28312631/article/details/47418773

2.最长上升子序列(百练2757)

问题描述

      一个数的序列ai，当a < a2 < ... < as的时候，我们称这个序列是上升的。对于给定的一个序列(a1，a2,  an)，我们可以得到一些上升的子序列(ai1，  ai2,  aik)，这里1 <=i1 （注：序列可以是隔着的，不一定是连续的）。比如，对于序列(1，7,  3，5,  9,  4,  8),有它的一些上升子序列，如(1，7)，(3， 4，  8)等等。这些子序列中最长的长度是4，比如子序列(1，3，5,  8)。

      要求对于给定的序列，求出最长上升子序列的长度。

输入数据：
输入的第一行是序列的长度N (1<= N <= 1000)。第二行给出序列中的N个整数，这些整数的取值范围都在0到10000。
输出要求：
最长上升子序列的长度。

输入样例

7
1 7 3 5 9 4 8

输出样例

4

解题思路：

1.找子问题
    “求序列的前n个元素的最长上升子序列的长度”是个子问题，但这样分解子问题，不具有“无后效性”。
    原因：假设F(n) =x, 但可能有多个序列满足F(n) = x。  有的序列的最后一个元素比an+1小， 则加上an+1就能形成更长上升子序列;有的序列最后一个元素不比an+1小......以后的事情受如何达到状态n的影响，不符合“无后效性”。

那么我们再换一个子问题。

 

求以ak (k=1，2，3，...，N)为终点的最长上升子序列的长度。
一个上升子序列中最右边的那个数，称为该子序列的“终点”。
虽然这个子问题和原问题形式上并不完全一样，但是只要这N个子问题都解决了，那么这N个子问题的解中，最大的那个就是整个问题的解。

2.确定状态

子问题只和一个变量——数字的位置相关。因此序列中数的位置k就是“状态”，而状态k对应的“值”，就是以ak作为“终点”的最长上升子序列的长度。

状态一共有N个。

3.找出状态转移方程：

maxLen(k)表示以ak做为“终点”的最长上升子序列的长度那么：

初始状态：maxLen(1)=1

maxLen(k)=max{ maxLen(i):1<=i

                   若找不到这样的i，则maxLen(k)=1（若不存在这样的i，说明在ak左边所有的数都是大于ak的，则以ak为“终点”的最长子序列为它自己）

因为ak左边任何“终点”小于ak的子序列，加上ak后就能形成一个更长的上升子序列。所以maxLen(k)的值，就是 在ak左边 ，“终点”数值小于ak ,且 长度最大 的那个上升子序列的长度再加一。 

/*
输入样例
7
1 7 3 5 9 4 8
输出样例
4
*/
#include
#include
using namespace std;
const int maxn=1005;
int a[maxn];
int maxLen[maxn];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	maxLen[1]=1;
	for(int k=2;k<=n;k++)//每次求第k个数为终点的最长上升子序列的长度
	{
		maxLen[k]=1;//初始化为1。即若找不到 a[i]ans)
			ans=maxLen[i];
	}
	cout<

算法时间复杂度：

时间复杂度=状态数组 * 计算一个状态的值所花的时间=N*O（N）=O(N^2)

(注计算一个状态所花的时间是for(int i=1;i

动归的常用两种形式

1)递归型
优点:直观，容易编写（一般思路都是递归的）
缺点:可能会因递归层数太深导致爆栈，函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说， 比递推型慢。
1)递推型
效率高，有可能使用滚动数组节省空间（如数字三角形题）。

3.最长公共子序列(POJ1458)

给出两个字符串，求出这样的一个最长的公共子序列的长度：子序列中的每个字符都能在两个原串中找到，而且每个字符的先后顺序和原串中的先后顺序一致。（与最长上升子序列一样，也是可以隔着的，不一定是连续的）

输入示例：

abdfbc abfcab

programming contest

abcd mnp

输出示例：

4(abcb)

2(on)

0

4.神奇的口袋

有一个神奇的口袋，总的容积是40，用这个口袋可以变出一些物品，这些物品的总体积必须是40。

John现在有n (1≤n≤20)个想要得到的物品，每个物品的体积分别是a1,a2,a3,......an。  John可以从这些物品中选择一些，如果选出的物体的总体积是40，那么利用这个神奇的口袋，John就可以得到这些物品。现在的问题是，John有 多少种不同的选择物品的方式。
题意总结：从体积分别是a1,a2,a3,......an的物体中选择若干个（每个物体只能选一次）凑成总体积是40，有多少种凑法。
输入：
输入的第一行是正整数n(1 <=n<= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2,......, an的值。

输出：
输出不同的选择物品的方式的数目。
输入样例：

3

20

20

20

输出样例：

3

1.枚举的解法：

枚举每个物品是选还是不选，共2^20种情况。

2.递归解法

/*
输入样例：
3
20
20
20
输出样例：
3*/ 
#include 
using namespace std;
int a[25];
int n;
int Ways(int w,int k)//从前k种物品中选择一些，凑成体积w的做法数目
{
	if(w==0) 
		return 1;//边界条件。若体积为0，则有一种选择法，即哪个物品都不选
	if(k<=0) 
		return 0;//边界条件。体积w仍不等于0（若w==0就return 1了)，但物品数已经小于等于零了，则说明无法凑
	//若不满足以上两个边界条件，则处理第k个物品,即选第k种物品和不选第k种物品 
	return Ways(w,k-1)+Ways(w-a[k],k-1);//注意是相加 
} 
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)//a[k]对应第k种物品  
	{
		cin>>a[i];
	}
	cout<

3.动归解法

递归解法中的边界条件就是动归解法中的初始值。

/*
输入样例：
3
20
20
20
输出样例：
3*/ 
#include
using namespace std;
int n;
int a[25];
int Ways[40][25];//Ways[w][k]表示从前k种物品中选择一些，凑成体积w的做法数目 
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) 
	{
		cin>>a[i];
	}
	for(int i=0;i<=n;i++) 
	{
		Ways[0][i]=1;//只要w是零，不管有几种物品，都是一种凑法 
	}
	for(int i=1;i<=40;i++) 
	{
		Ways[1][0]=0;//w不是零，有0种物品则无法凑成
	}
	for(int w=1;w<=40;w++)
	{
		for(int k=1;k<=n;k++)
		{
			if(w>=a[k])//若可以挑选 
				Ways[w][k]=Ways[w][k-1]+Ways[w-a[k]][k-1];
			else//不能挑选
				Ways[w][k]=Ways[w][k-1]; 
		}
	}
	cout<

5. 01背包问题（poj3624）

有n件物品和一个容积为m的背包。第i件物品的体积是w[i]，价值是d[i]。求解哪些物品装入背包可使价值总和最大，输出最大的价值总和。每种物品只有一件，可以选择放或者不放。(n<=1000,m<=13000)

注意此题和上一题神奇的口袋题的不同，这个不用非得凑成容积m，只要总体积小于等于m即可。重点是使价值总和最大。

Sum[w][k]表示取前k种物品，使它们总体积不超过w的最优取法取得的价值总和。要求Sum[m][n]。

/*
输入示例
4 5
2 3
1 2
3 4
2 2
输出示例
7
(挑选第1,2,4件) 
*/
#include 
using namespace std;
int w[1005];
int d[1005];
int n,m;
int Sum[13000][1005];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>w[i]>>d[i];
	}
	for(int i=0;i<=40;i++) 
	{
		Sum[i][0]=0;//若从0种物品中选，则最大价值总和为0 
	}
	for(int we=1;we<=m;we++)
	{
		for(int k=1;k<=n;k++)
		{
			if(we>=w[k])
				Sum[we][k]=max(Sum[we][k-1],Sum[we-w[k]][k-1] + d[k]);
			else
				Sum[we][k]=Sum[we][k-1];
		}
	}
	cout<