机器学习——决策树（ID3、C4.5、CART）

---

以下均为个人理解，如有错误，欢迎指出。

---

什么是决策树

引自维基百科我是链接

决策树（Decision tree）由一个决策图和可能的结果（包括资源成本和风险）组成， 用来创建到达目标的规划。决策树建立并用来辅助决策，是一种特殊的树结构。决策树是一个利用像树一样的图形或决策模型的决策支持工具，包括随机事件结果，资源代价和实用性。它是一个算法显示的方法，决策树分为分类树和回归树

来直观的了解一下分类树，假设我们有一批瓜，我们用纹理、触感、根蒂、色泽来描述这批瓜，现在我们想通过这几个特征去判断一个瓜是不是好瓜，决策树通过某些标准不断将这些瓜进行划分，例如以纹理为划分标准，获得一批子集，每个子集在根据某个标准（例如触感）进行划分，划分到一定程度后，停止划分，由此可得一系列的子集，这些子集可被整理成树形结构，最后，我们给树的叶子节点进行标注，表明这个叶子节点属于什么类别。
上述过程的决策树长下面这样（来自周志华老师的《机器学习》）：

图一

分类树需要解决的问题

决策树其实就是不断选择某个特征将一个集合划分为若干个子集，使得子集的纯度比父集合更高，由此想法出发，在我看来，决策树需要解决两个问题

1、如何衡量一个样本集的纯度？
若一个样本集中包含的样本的类别单一，我们就说这个样本集纯度高，举个例子，现在有20个西瓜，每十个为一组：
A：6个好瓜，4个坏瓜
B：9个好瓜，1个坏瓜
明显可以看出，B组的纯度更高，我们需要一个函数来量化一个样本集的纯度，由此可通过数值的大小判断样本集的纯度

2、如何判断使用哪个特征作为划分标准？
懂得如何量化纯度以后，我们需要一个东西，来判断我们选择哪个特征进行划分可以得到最大程度的纯度提升

ID3决策树（分类树）

ID3决策树通过信息熵度量样本集的纯度，通过信息增益判断应该选择哪个特征作为划分标准。

信息量

信息量用来衡量信息的多少，信息量长这样(log的底数不一定为2，但是ID3选择的是2)：

$-lo{g}_2(p(x))$

网上有许多直观的解释，但是总能想到该直观解释不能解释的例子，在此不解释信息量为什么长这样

度量样本集合纯度的指标——信息熵

记得是在《通信系统》一书中第一次接触信息熵，它长这样：

$Ent(D)=-{\sum }_{i=1}^{n}p(x_i)lo{g}_2(p(x_i))（式1.0）$

其中，$p(x_i)$表示事件$x_i$出现的概率，一般情况下，概率是通过频数去接近的，而频数等于事件$x_i$出现的次数除以总实验次数，信息熵可用来度量样本集合纯度，式1.0即为样本集合D的纯度，如果样本集合纯度越高，$Ent(D)$越趋近于0（直观来说，由于某个$p(x_i)$越趋近于1，则有$lo{g}_2(p(x_i))$趋近于0）

选择划分特征的指标——信息增益

为了得知划分前后纯度提升了多少，一个很自然的想法是用划分前的信息熵减去划分后每个子集信息熵的和，我们往更深处想，以图一来说，假设我们用触感作为划分标准，我们可以得到两个子集，一个子集的所有西瓜的触感为硬滑，另一个子集的所有西瓜的触感为软粘，我们是在已知每个子集触感的基础上计算这两个子集的信息熵的，类似于条件概率，也有条件熵存在，它长这样（图源自
维基百科）：

条件熵用于已知样本集合某些特征的基础上计算样本集合的纯度，上式中，$X$为选取的特征，$x$为该特征的取值，$p(y|x)$表示已知$X$特征取值为$x$的情况下,$Y$取值为$y$的概率，拿我们上面的例子来说，就是已知瓜的触感为硬滑（软粘）的情况下，是好（坏）瓜的概率，我们依然使用频数来粗略表示概率。

以下概念摘自周志华老师的《机器学习》

假定离散属性a有$V$个可能的取值$a^1,a^2,....,a^V$,若使用a来对样本集D进行划分，则会产生$V$个分支节点，记第$v$个分支的节点个数为$D^v$，则划分后各子集条件熵之和为：

${\sum }_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)（式1.1）$

则信息增益为：

$Gain(D,a)=Ent(D)-{\sum }_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)(式1.2)$

与信息熵一样，条件熵取值越小，表示该样本的纯度越高，故每次选择式1.2取值最大的属性作为划分标准

决定使用某个属性作为划分后，子集将不再考虑使用这个属性进行划分（因为同一子集的所有样本在该属性上的取值都相等）

ID3决策树的缺点

ID3决策树是最早提出的决策树算法，它有一个缺点——偏向于选择取值较多的属性作为划分节点，这是由式1.2的特性决定的，直观来说，对于取值多的属性，划分的子集数目必然较多，相较于取值较少的属性来说，部分子集含有的样本数量较少，这些子集的纯度较高，式1.2的取值会较小。举个例子，现在有6个样本，利用A特征进行划分，获得两个子集，样本个数均为3，假设两个子集的好瓜个数均为2，则其条件熵之和为：$\frac{2}{3}\ast lo{g}_2(\frac{3}{2})+\frac{1}{3}\ast lo{g}_{2}3$，利用B特征进行划分，获得6个子集，每个子集样本个数均为1，毫无疑问，其条件熵之和为0，信息增益将最大

C4.5决策树（分类树）

为了克服ID3的缺点，C4.5决策树诞生了，其仍然使用信息熵度量样本集合纯度。

选择划分特征的指标——增益率

式1.2的一个特点是属性的取值越多，式1.2的取值越大，一个自然而然的想法是能不能对式1.2进行改造，添加一个系数，该系数满足当属性的取值越多，该系数的取值越小，当属性取值较少，该系数的取值较大，这样可以缓解ID3的选择偏好，基于这样的想法，C4.5对信息增益施加了一个系数（“惩罚”）：

$IV(a)=-{\sum }_{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}（式1.3）$

这个式子是样本在属性a上取值的信息墒，如果样本在属性a上的取值多，那么纯度就低，式1.3取值就大，如果取值少，那么纯度就高，式1.3取值就小，之所以选择这个式子，我觉得可能是一种折中的选择，对于取值较多的属性施加的"惩罚"大于取值较小的属性，决策树可能会更偏向于选择取值较小的属性，而式1.3可以较好的平衡这两种选择偏好

C4.5对式1.2进行改造得到增益率：

$Grain\_ratio(D,a)=\frac{Grain(D,a)}{IV(a)}（式1.4）$

虽然式1.3可以较好的平衡决策树的两种选择偏好，但式1.3仍然偏向于选择取值较少的属性，为了克服这个缺点，C4.5使用了一个启发式的算法，先从划分属性中选出信息增益高于平均水平的属性，接着选择信息增益率最高的属性作为划分标准

决定使用某个属性作为划分后，子集将不再考虑使用这个属性进行划分（因为同一子集的所有样本在该属性上的取值都相等）

CART决策树（分类树）

CART决策树可以做分类也可以做回归，和C4.5、ID3不同的是，它是一个二叉树

度量样本集合纯度的指标——基尼值

CART使用基妮值来度量样本集的纯度，对于有$|\gamma |$个类别的样本集D来说，其基尼值如下：

$Gini(D)=1-{\sum }_{k=1}^{|\gamma |}{p}_k^2（式1.5）$

样本集D中，类别$i$的个数为k，样本集D含有n个样本，我们从样本集中随机抽取两个物品，同属于类别$i$的概率为$\frac{k}{n}\ast \frac{k-1}{n-1}$，当样本集D很大时，$\frac{k}{n}\approx \frac{k-1}{n-1}$，此时，基尼值反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率

选择划分特征的指标——基尼指数

使用$D_1$表示样本集D上属性A取值为$a$的样本集，$D_2$表示样本集D上属性A取值不为$a$的样本集。此时，基尼指数取值为：

$Gini\_index(D,A,a)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)（式1.6）$

我们倾向于选择基尼指数小的属性的取值作为划分指标，决定使用某个属性某个取值作为划分指标后，例如选择A属性的取值a进行划分，将把一个集合划分为两个子集合，一个子集合中的所有样本在属性A上的取值均为a，一个子集合中的所有样本在属性A上的取值不为a

为什么选择基尼指数

无论是ID3，还是C4.5，它们均使用信息熵来度量样本的纯度，信息熵中存在log，在计算机中，log运算会花费较长时间，那么有没有什么方式减少这个开销呢？于是基尼指数横空出世，下图显示了信息增益的一半（熵之半）、Gini指数，分类误差率的图像：

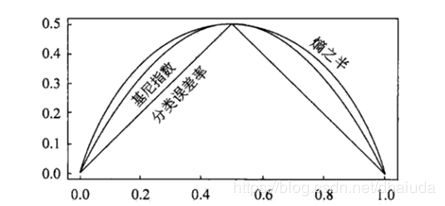
可以看到，这三者非常接近（图像看上去有一段距离，但这段距离可能就是零点几的差距），并且信息增益的一半并不会影响最终的选择结果（由于所有属性的信息增益都减少了一半，相对大小没有发生改变），所以我们可以用基尼指数去近似表示信息增益，由此来看，CART与ID3在样本纯度和划分特征的公式选取上并没有太大差别，但是CART的计算速度会比ID3快（直观上来看，CART树似乎也会偏向于选择取值较多的属性）

分类树的构建过程

设当前节点集为D，候选划分属性集为A。递归构建分类树

函数TreeGenerate（D，A）
生成节点node
if D中所有样本属于同一类C
	将node节点作为叶子节点，类别标记为C
	return
if A为空集 or D对A的所有属性取值都相同
	将node节点作为叶子节点，类别标记为D中样本数最多的类
	return
从A中选择最优的划分属性a
for a的每一个值a_v do
	为node生成一个分支节点，令Dv表示D上a属性取值为a_v的样本子集
	if Dv为空
		将该分支节点标记为D中样本数最多的类
	else
		分支节点=TreeGenerate（Dv，A\{a}）

CART决策树（回归树）

CART回归树用于回归分析

算法流程

假设我们有一批样本，每组样本有n个自变量，1个因变量，第i个样本用
{$x_{i1},x_{i2},.....,x_{in},y_i$}表示
1、对于当前集合，选择一个特征 $j$ 以及其上的一个切分点s（s的选取可以是当前集合该特征上的每个取值），若样本的第j个特征取值小于s，则归为R1子类，否则，归为R2子类
2、计算两个子类的因变量方差，将方差相加，记为${\delta }_{js}$，步骤1、2可以使用$(j,s,{\delta }_{js})$表示
3、重复步骤1、2，可得当前集合下，所有特征、所有切分点对应的方差，选择最小的方差，可获得该方差对应的特征$k$和切分点$s$，将样本集上特征k的取值小于$s$的归为R1，大于等于$s$的归为R2，我们用当前节点的所有样本的因变量的均值表示该节点的输出
4、对R1和R2重复步骤1~3，直到满足停止条件（例如当前所有节点的输出与真实值的均方误差小于某个特定的值）
一个例子：https://cethik.vip/2016/09/21/machineCAST/

如何进行预测

对于一个新的样本$p$，即{$x_{p1},x_{p2},.....,x_{pn},y_p$}，从决策树的根部开始，假设当前决策树节点选择特征 $j$ 上的 取值$s$作为切分点，若$x_{pj}$小于$s$,则归为R1节点，否则，归为R2节点，在新的节点上不断进行上述步骤，直到到达叶子节点，叶子节点所有样本的因变量的均值即为样本$p$的预测值

个人理解

CART回归树有点分类树的味道，每一次划分都是为了让处于同一节点的样本的因变量相较于其他划分来说更为紧密，所以我们用方差作为划分标准。直观来看，CART决策树试图通过不断的划分，使同一节点的样本的因变量越来越接近，最后可用样本均值来表示节点的输出

分类树如何处理连续值

由于连续属性的取值个数不在有限，因此，不能直接根据连续属性的可取值对节点划分，连续值离散化的技术有很多，这里介绍最简单的二分法
以下内容摘自周志华老师的《机器学习》

给定样本集D和连续属性a，设a在D上的$v$个取值为 {$a^1,a^2,a^3,....,a^n$},我们可以选定一个值t，小于t的归为一个子集，大于t的归为另一个子集，对于相邻取值$a^i,a^{i+1}$来说，t在区间[$a^i,a^{i+1}$)任何一个地方的产生的划分结果都一致，因此，我们将相邻取值的中值构成的集合作为t的候选集，如下：

$T_a=\{\frac{(a^i+a^{i+1})}{2}|1\le i\le n-1\}$(式1.4)

接下来的处理过程就和之前介绍的算法一样了

由于决策树只是要求划分后的集合纯度提升，因此使用二分法将连续值离散化并不会与决策树的初衷违背

防止过拟合

• 什么是决策树的过拟合

以下内容摘自周志华老师的《机器学习》
在决策树的学习过程中，节点划分过程不断进行，有时会导致决策树分支节点过多，这是就可能因训练样本学得“太好”了，以致于把训练集自己的一些特点当作所有数据都具有的一般性质

从概念上看，出现过拟合的原因是决策树分支过多，即分类过细。一个很自然的想法便是减少决策树的分支树，这就是决策树的剪枝，决策树的剪枝分为预剪枝和后剪枝

我们将样本集分为训练集和测试集

预剪枝

做法：首先选择划分属性，接着使用测试集测试节点划分前后的准确率，如果准确率没有提高，则停止划分，用该节点所含数目最多的类别标记该节点，否则，进行划分。
优点：使决策树的很多节点没有展开，减少训练时间和测试时间，减少了过拟合的风险
缺点：有些节点的当前划分虽然不能提升泛化性能，但是在此划分的基础上，后续的划分可能会提高决策树的泛化功能，使用预剪枝可能会造成欠拟合

后剪枝

做法：将决策树训练好后，自底向上的决定节点是否要进行划分，用测试集测试划分前后的准确率，如果精准度提高，则去除该节点的分支，用该节点所含数目最多的类别标记该节点，如果划分前后准确率没有变化，根据奥卡姆剃刀准则，我们依然会选择剪枝
优点：防止过拟合的同时防止欠拟合
缺点：训练时间长

决策树的几何意义

从上述算法的过程可以明显看出，决策树每次选择一个特征进行划分，即用平行于该特征对应的坐标轴的直线来划分训练集，对于二特征样本集来说，决策树训练的结果如下（图源自《机器学习》）：

决策树的优缺点

总结自维基百科

优点
1、不需要数据归一化
2、可以处理连续型、离散型数据
3、模型可解释
4、可以很好的处理大规模数据

缺点
1、训练一科最优决策树是完全NP问题，上述算法都是采用贪心策略构建
2、有些问题没法通过决策树很好解决，例如异或类问题，这类问题往往会让决策树变得很大

分类树与逻辑回归的比较

从几何意义上看，分类树比逻辑回归粒度更细，逻辑回归只是使用一条直线去划分数据集，而分类树使用多条平行与坐标轴的直线划分，粒度自然够细，一般情况下，如果数据集可以通过一条非平行于坐标轴的直线大致划分，则使用逻辑回归，否则，可以考虑使用分类树