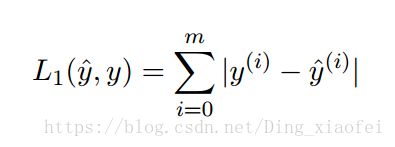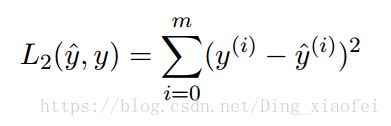吴恩达DeepLearning.ai课程编程实践(一)
开篇
同样作为深度学习的入门系列博客吧,希望闲时能够花个不到一个小时理一下吴恩达老师课程里面涉及到的编程,当然学习这些知识的前提是,你能够使用python编程。这边我不限定内容的长短,每篇不完成固定的内容,如果不全,那么就下篇再见。
sigmoid function
常见的激活函数,缺点就不提了,二分类任务的输出层比较常见,下面是它的函数图
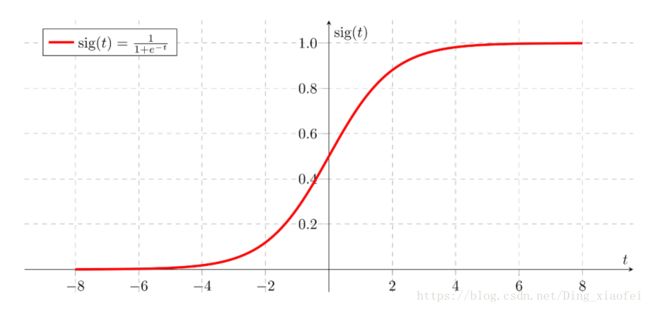
它的实现
import math
def basic_sigmoid(x):
"""
Compute sigmoid of x.
Arguments:
x -- A scalar
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### ( 1 line of code)
s = 1/(1+math.exp(-x))
### END CODE HERE ###
return s这里的话对于向量就不太友好啦,我们深度学习中做向量化最终的目的就是为了并行。所以使用numpy去实现它更加合适
# GRADED FUNCTION: sigmoid
import numpy as np
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### ( 1 line of code)
s = 1/(1+np.exp(-x))
### END CODE HERE ###
return s
x = np.array([1,2,3])
sigmoid(x)
#output
array([ 0.73105858, 0.88079708, 0.95257413])numpy会为我们实现向量的这种广播式计算,计算效率会比较高。
sigmoid gradient
def sigmoid_derivative(x):
s = 1/(1+np.exp(-x))
ds = s*(1-s)
return dsreshape
神经网络中张量维度经常需要相应的操作
v = v.reshape((v.shape[0]*v.shape[1], v.shape[2]))def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length,height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
### START CODE HERE ### ( 1 line of code)
v = image.reshape((image.shape[0]*image.shape[1]*image.shape[2]),1)
### END CODE HERE ###
return v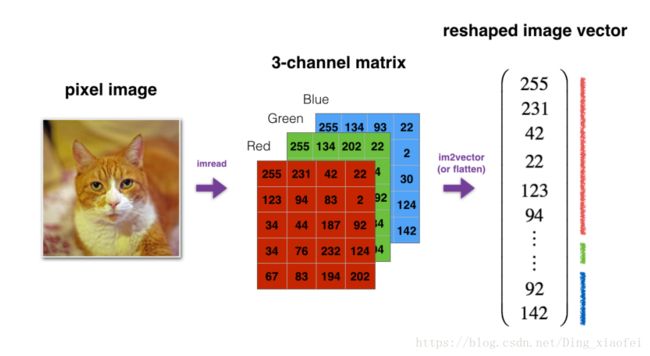
相信看了上图,你会明白上面代码讲的意思,大家可以自己试一试代码的效果。
Normalizing rows
# GRADED FUNCTION: normalizeRows
def normalizeRows(x):
x_norm=np.linalg.norm(x,axis=1,keepdims=True)
# Divide x by its norm.
x = x/x_norm
### END CODE HERE ###
return x
x = np.array([
[0, 3, 4],
[1, 6, 4]])
print("normalizeRows(x) = " + str(normalizeRows(x)))
#output
normalizeRows(x) = [[ 0. 0.6 0.8 ]
[ 0.13736056 0.82416338 0.54944226]]softmax function
def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp,axis = 1,keepdims = True)
s = x_exp/x_sum
return sL1 and L2 loss function
def L1(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
12
Returns:
loss -- the value of the L1 loss function defined above
"""
loss = sum(abs(y-yhat))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))def L2(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L2 loss function defined above
"""
loss = np.dot(y-yhat,y-yhat)
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))ok,短了点,就先到这里吧。