机器学习笔记(二):一个完整的机器学习项目(上)
开篇
依旧是机器学习实用指南的笔记,这边主要是第二章节的内容,希望通过代码和一些实例带大家去了解一个完整的机器学习项目,笔记主要是提炼要点,想要看原文的请点击。
要点
分层采样生成测试集
主要步骤:
项目概述。
获取数据。
发现并可视化数据,发现规律。
为机器学习算法准备数据。
选择模型,进行训练。
微调模型。
给出解决方案。
部署、监控、维护系统。
获取查看数据
关于如何获取数据就算了,去它的github下载就好了,我们直接看看我们的数据是什么样子的。
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)每一行都表示一个街区。共有 10 个属性(截图中可以看到 6 个):经度、维度、房屋年龄中位数、总房间数、总卧室数、人口数、家庭数、收入中位数、房屋价值中位数、离大海距离。
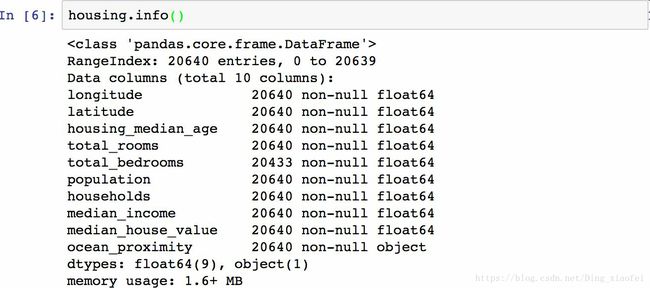
info()方法可以快速查看数据的描述,特别是总行数、每个属性的类型和非空值的数量。
数据集中共有 20640 个实例,按照机器学习的标准这个数据量很小,但是非常适合入门。我们注意到总房间数只有 20433 个非空值,这意味着有 207 个街区缺少这个值。我们将在后面对它进行处理。
所有的属性都是数值的,除了离大海距离这项。它的类型是对象,因此可以包含任意 Python 对象,但是因为该项是从 CSV 文件加载的,所以必然是文本类型。在刚才查看数据前五项时,你可能注意到那一列的值是重复的,意味着它可能是一项表示类别的属性。可以使用value_counts()方法查看该项中都有哪些类别,每个类别中都包含有多少个街区:
>>> housing["ocean_proximity"].value_counts()
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
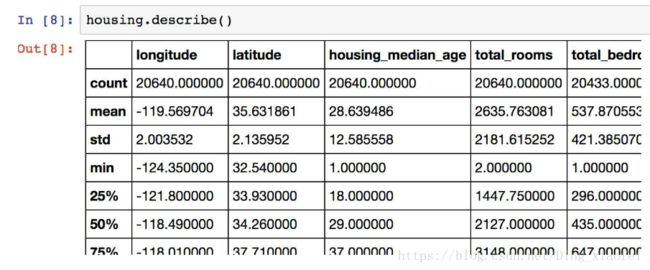
Name: ocean_proximity, dtype: int64再来看其它字段。describe()方法展示了数值属性的概括
count、mean、min和max几行的意思很明显了。注意,空值被忽略了(所以,卧室总数是 20433 而不是 20640)。std是标准差(揭示数值的分散度)。25%、50%、75% 展示了对应的分位数:每个分位数指明小于这个值,且指定分组的百分比。例如,25% 的街区的房屋年龄中位数小于 18,而 50% 的小于 29,75% 的小于 37。这些值通常称为第 25 个百分位数(或第一个四分位数),中位数,第 75 个百分位数(第三个四分位数)。
另一种快速了解数据类型的方法是画出每个数值属性的柱状图。柱状图(的纵轴)展示了特定范围的实例的个数。你还可以一次给一个属性画图,或对完整数据集调用hist()方法,后者会画出每个数值属性的柱状图(见图 2-8)。例如,你可以看到略微超过 800 个街区的median_house_value值差不多等于 500000 美元。
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()注意柱状图中的一些点:
- 首先,收入中位数貌似不是美元(USD)。与数据采集团队交流之后,你被告知数据是经过缩放调整的,过高收入中位数的会变为 15(实际为15.0001),过低的会变为 5(实际为 0.4999)。在机器学习中对数据进行预处理很正常,这不一定是个问题,但你要明白数据是如何计算出来的。
房屋年龄中位数和房屋价值中位数也被设了上限。后者可能是个严重的问题,因为它是你的目标属性(你的标签)。你的机器学习算法可能学习到价格不会超出这个界限。你需要与下游团队核实,这是否会成为问题。如果他们告诉你他们需要明确的预测值,即使超过
500000 美元,你则有两个选项:- 对于设了上限的标签,重新收集合适的标签;
- 将这些街区从训练集移除(也从测试集移除,因为若房价超出 500000 美元,你的系统就会被差评)。
- 这些属性值有不同的量度。我们会在本章后面讨论特征缩放。
- 最后,许多柱状图的尾巴很长:相较于左边,它们在中位数的右边延伸过远。对于某些机器学习算法,这会使检测规律变得更难些。我们会在后面尝试变换处理这些属性,使其变为正态分布。
创建测试集
在这个阶段就分割数据,听起来很奇怪。毕竟,你只是简单快速地查看了数据而已,你需要再仔细调查下数据以决定使用什么算法。这么想是对的,但是人类的大脑是一个神奇的发现规律的系统,这意味着大脑非常容易发生过拟合:如果你查看了测试集,就会不经意地按照测试集中的规律来选择某个特定的机器学习模型。再当你使用测试集来评估误差率时,就会导致评估过于乐观,而实际部署的系统表现就会差。这称为数据透视偏差。
理论上,创建测试集很简单:只要随机挑选一些实例,一般是数据集的 20%,放到一边:
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]>>> train_set, test_set = split_train_test(housing, 0.2)
>>> print(len(train_set), "train +", len(test_set), "test")
16512 train + 4128 test这个方法可行,但是并不完美:如果再次运行程序,就会产生一个不同的测试集!多次运行之后,你(或你的机器学习算法)就会得到整个数据集,这是需要避免的。
解决的办法之一是保存第一次运行得到的测试集,并在随后的过程加载。另一种方法是在调用np.random.permutation()之前,设置随机数生成器的种子(比如np.random.seed(42)),以产生总是相同的洗牌指数(shuffled indices)。
但是如果数据集更新,这两个方法都会失效。一个通常的解决办法是使用每个实例的ID来判定这个实例是否应该放入测试集(假设每个实例都有唯一并且不变的ID)。例如,你可以计算出每个实例ID的哈希值,只保留其最后一个字节,如果该值小于等于 51(约为 256 的 20%),就将其放入测试集。这样可以保证在多次运行中,测试集保持不变,即使更新了数据集。新的测试集会包含新实例中的 20%,但不会有之前位于训练集的实例。下面是一种可用的方法:
import hashlib
def test_set_check(identifier, test_ratio, hash):
return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
return data.loc[~in_test_set], data.loc[in_test_set]不过,房产数据集没有ID这一列。最简单的方法是使用行索引作为 ID:
housing_with_id = housing.reset_index() # adds an `index` column
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")如果使用行索引作为唯一识别码,你需要保证新数据都放到现有数据的尾部,且没有行被删除。如果做不到,则可以用最稳定的特征来创建唯一识别码。例如,一个区的维度和经度在几百万年之内是不变的,所以可以将两者结合成一个 ID:
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")Scikit-Learn 提供了一些函数,可以用多种方式将数据集分割成多个子集。最简单的函数是train_test_split,它的作用和之前的函数split_train_test很像,并带有其它一些功能。首先,它有一个random_state参数,可以设定前面讲过的随机生成器种子;第二,你可以将种子传递给多个行数相同的数据集,可以在相同的索引上分割数据集(这个功能非常有用,比如你的标签值是放在另一个DataFrame里的):
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)目前为止,我们采用的都是纯随机的取样方法。当你的数据集很大时(尤其是和属性数相比),这通常可行;但如果数据集不大,就会有采样偏差的风险。当一个调查公司想要对 1000 个人进行调查,它们不是在电话亭里随机选 1000 个人出来。调查公司要保证这 1000 个人对人群整体有代表性。例如,美国人口的 51.3% 是女性,48.7% 是男性。所以在美国,严谨的调查需要保证样本也是这个比例:513 名女性,487 名男性。这称作分层采样(stratified sampling):将人群分成均匀的子分组,称为分层,从每个分层去取合适数量的实例,以保证测试集对总人数有代表性。如果调查公司采用纯随机采样,会有 12% 的概率导致采样偏差:女性人数少于 49%,或多于 54%。不管发生那种情况,调查结果都会严重偏差。
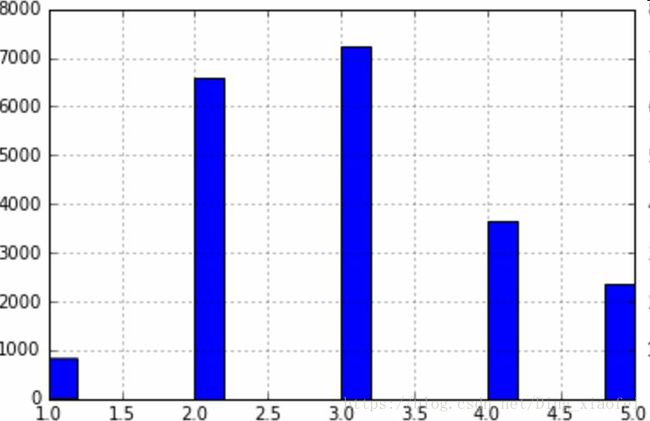
假设专家告诉你,收入中位数是预测房价中位数非常重要的属性。你可能想要保证测试集可以代表整体数据集中的多种收入分类。因为收入中位数是一个连续的数值属性,你首先需要创建一个收入类别属性。再仔细地看一下收入中位数的柱状图(图 2-9)(译注:该图是对收入中位数处理过后的图):
大多数的收入中位数的值聚集在 2-5(万美元),但是一些收入中位数会超过 6。数据集中的每个分层都要有足够的实例位于你的数据中,这点很重要。否则,对分层重要性的评估就会有偏差。这意味着,你不能有过多的分层,且每个分层都要足够大。后面的代码通过将收入中位数除以 1.5(以限制收入分类的数量),创建了一个收入类别属性,用ceil对值舍入(以产生离散的分类),然后将所有大于 5的分类归入到分类 5:
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace=True)这里写第一行代码的时候报错,主要是有个东西没有装
使用命令
conda install mkl-rt装完就没事啦
现在,就可以根据收入分类,进行分层采样。你可以使用 Scikit-Learn 的StratifiedShuffleSplit类:
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]参数说明
from sklearn.model_selection import StratifiedShuffleSplit
StratifiedShuffleSplit(n_splits=10,test_size=None,train_size=None, random_state=None)参数 n_splits是将训练数据分成train/test对的组数,可根据需要进行设置,默认为10
参数test_size和train_size是用来设置train/test对中train和test所占的比例。例如:
1.提供10个数据num进行训练和测试集划分
2.设置train_size=0.8 test_size=0.2
3.train_num=num*train_size=8 test_num=num*test_size=2
4.即10个数据,进行划分以后8个是训练数据,2个是测试数据
注:train_num≥2,test_num≥2 ;test_size+train_size可以小于1
参数 random_state控制是将样本随机打乱
关于这个函数的更多说明。
检查下结果是否符合预期。你可以在完整的房产数据集中查看收入分类比例:
>>> housing["income_cat"].value_counts() / len(housing)
3.0 0.350581
2.0 0.318847
4.0 0.176308
5.0 0.114438
1.0 0.039826
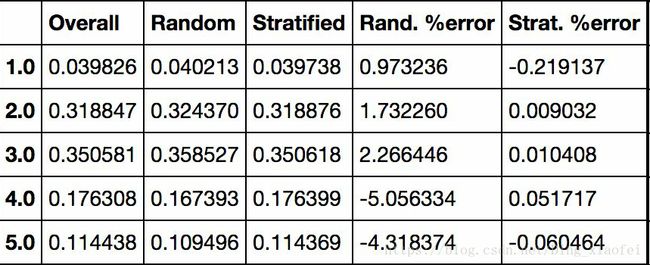
Name: income_cat, dtype: float64使用相似的代码,还可以测量测试集中收入分类的比例。图 2-10 对比了总数据集、分层采样的测试集、纯随机采样测试集的收入分类比例。可以看到,分层采样测试集的收入分类比例与总数据集几乎相同,而随机采样数据集偏差严重。
图 2-10 分层采样和纯随机采样的样本偏差比较
现在,你需要删除income_cat属性,使数据回到初始状态:
for set in (strat_train_set, strat_test_set):
set.drop(["income_cat"], axis=1, inplace=True)我们用了大量时间来生成测试集的原因是:测试集通常被忽略,但实际是机器学习非常重要的一部分。还有,生成测试集过程中的许多思路对于后面的交叉验证讨论是非常有帮助的。接下来进入下一阶段:数据探索。
数据探索和可视化、发现规律
目前为止,你只是快速查看了数据,对要处理的数据有了整体了解。现在的目标是更深的探索数据。
首先,保证你将测试集放在了一旁,只是研究训练集。另外,如果训练集非常大,你可能需要再采样一个探索集,保证操作方便快速。在我们的案例中,数据集很小,所以可以在全集上直接工作。创建一个副本,以免损伤训练集:
housing = strat_train_set.copy()地理数据可视化
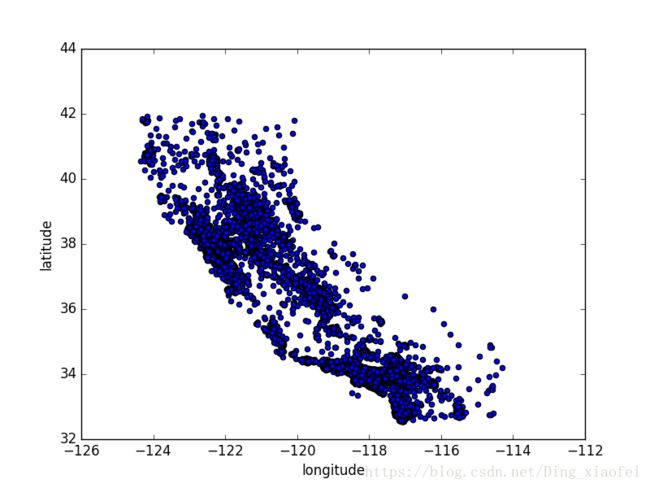
因为存在地理信息(纬度和经度),创建一个所有街区的散点图来数据可视化是一个不错的主意(图 2-11):
housing.plot(kind="scatter", x="longitude", y="latitude")
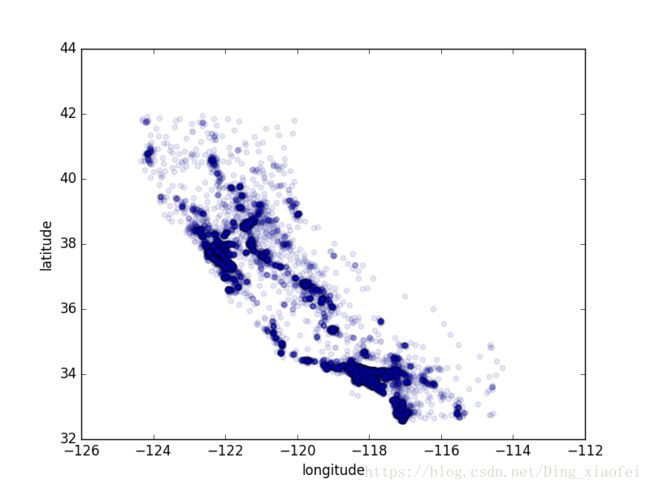
plt.show()这张图看起来很像加州,但是看不出什么特别的规律。将alpha设为 0.1,可以更容易看出数据点的密度
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)现在看起来好多了:可以非常清楚地看到高密度区域,湾区、洛杉矶和圣迭戈,以及中央谷,特别是从萨克拉门托和弗雷斯诺。
通常来讲,人类的大脑非常善于发现图片中的规律,但是需要调整可视化参数使规律显现出来。
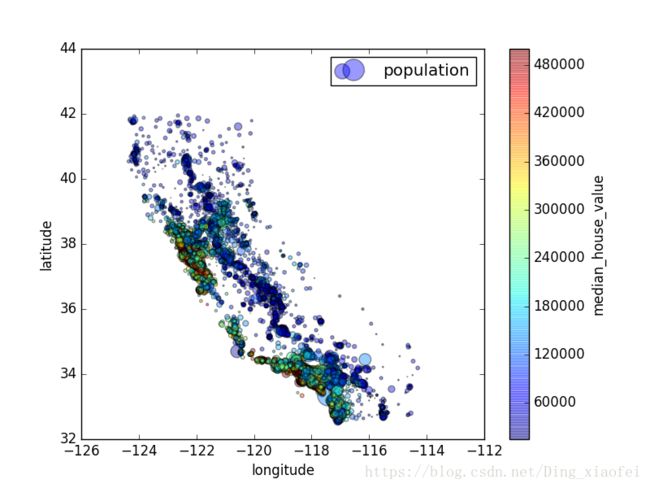
现在来看房价。每个圈的半径表示街区的人口(选项s),颜色代表价格(选项c)。我们用预先定义的名为jet的颜色图(选项cmap),它的范围是从蓝色(低价)到红色(高价):
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population",
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)
plt.legend()这张图说明房价和位置(比如,靠海)和人口密度联系密切,这点你可能早就知道。可以使用聚类算法来检测主要的聚集,用一个新的特征值测量聚集中心的距离。尽管北加州海岸区域的房价不是非常高,但离大海距离属性也可能很有用,所以这不是用一个简单的规则就可以定义的问题。
(未完6.9更新)