DAT（NIPS 2018）视频目标跟踪论文笔记

1. 论文基本信息

• 论文标题：Deep Attentive Tracking via Reciprocative Learning
• 论文作者：Shi Pu（Beijing University of Posts and Telecommunications）等人
• 论文出处：NIPS 2018
• 在线阅读：https://arxiv.org/pdf/1810.03851.pdf
• 源码链接：https://github.com/shipubupt/NIPS2018

---

2. 概述

论文通过在深度学习损失函数中引入注意力正则（attention regularization），并且利用reciprocative learning进行反向传播训练得到attention map，该attention map会影响跟踪过程中产生的classification score，从而实现更加鲁棒的跟踪算法。

---

3. 研究动机

(1) 有的跟踪算法采用固定形态的空间加权作为注意力机制，不够灵活，难以适应目标的显著运动。

传统采用了视觉注意力的跟踪方法，有些采用了某种特定形态的空间加权（e.g. CF2采用的cosine窗函数，SRDCF采用高斯函数），这一类方法往往给予中央区域更高的权重，为周边区域分配较低的权重，这里以SRDCF为例，其空间加权如下图所示（注： SRDCF里面用的是惩罚权重，因此plot中的数值越高的部分表示惩罚越大）：

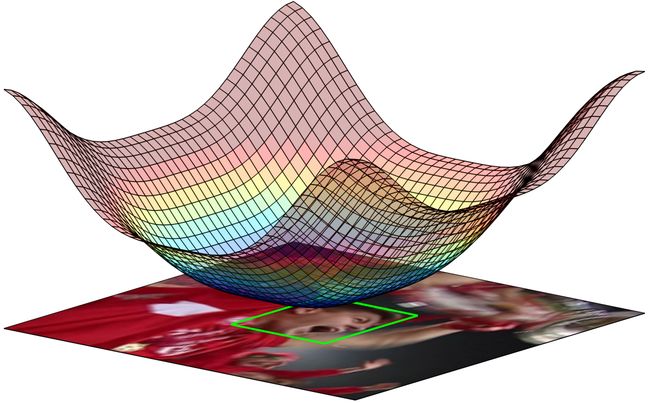
可以推测，在这种注意力机制下，在目标物体发生显著位移时会影响跟踪的效果（因为目标如果发生显著位移，会出现在采样区域的边缘，权重降低后容易被跟踪器标记为背景信息）。

(2) 有的跟踪算法利用附加的注意力模块来实现单一视频帧的特征加权，难以实现时间维度上的鲁棒性。

举例，STAM和HART跟踪算法就采用了额外的注意力模块来生成特征权重，然而，这些权重都是基于单帧视频（通常都用current frame）画面学习得到的，在目标物体的运动过程中，它们难以集中到稳定、鲁棒的信息上来。并且，如果特征加权中出现了少量偏差，就有可能导致分类错误。

---

4. 提出的方法

不同于现有的注意模型利用附加模块来生成注意力数据，论文作者使用网络输出关于输入图像的偏导数作为注意力图。论文使用attention map作为training阶段的正则项，使分类器学习到对外观变化具有鲁棒性的区域（这部分区域就是注意力）。在测试过程中，论文直接使用深度网络输出的得分来定位目标对象。论文的总体结构如下图所示：

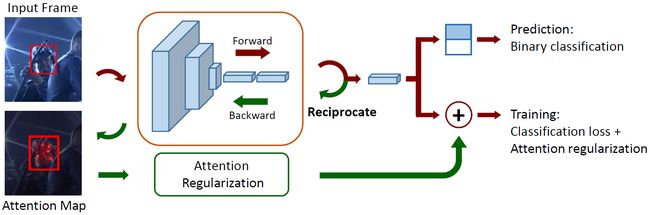
论文提出的方法总体上可以分为四个步骤：

1. 输入一幅training图像，首先通过前向传播计算classification score。
2. 根据上述classification score，利用反向传播计算关于输入图像偏导数的方式，得到attention map（此反向传播不更新网络参数，仅仅只是为了得到attention map）。
3. 将上述attention map作为深度网络损失函数正则项，迭代训练深度网络（此反向传播更新网络参数）。
4. 在testing阶段，直接利用上述迭代训练好的深度网络作正向传播，进行目标物体定位。

4.1 Attention Exploitation（对应总体步骤1 - 2）

CNN网络的前向传播，可以用一阶泰勒展开（first-order Taylor expansion）进行描述，如下所示：
$$f_c\left(I\right)\approx A_c^{\top }I+B\text{\hspace{1em}(1)}$$
其中，$I$表示输入的图像，$c$表示某一特定的类别class，$f_c$表示CNN网络输出，其含义是：输入图像属于类别$c$的可能性。$A_c^{\top }$表示网络相对于输入$I$的梯度，$B$表示偏置。对于$A_c^{\top }$，它可以表示为：
$$A_c={\frac{\partial f_c\left(I\right)}{\partial I}|}_{I=I_0}\text{\hspace{1em}(2)}$$

从公式(1)可以看出：

1. 输入$I$的类别$c$得分受$A_c$元素值的影响。
2. $A_c$内部的元素值表明输入图像$I_0$的相应像素对最终类别得分的贡献度（输入图像目标区域的贡献度高，背景区域的贡献度低）。

这样，我们就可以将$A_c$看做是一个attention map。并且从$A_c$的定义可知，对于不同的输入图像，其值是特定的。

根据公式(2)，论文通过计算输出$f_c\left(I\right)$关于输入$I_0$的偏导数来求解$A_c$，这当中包含了两个步骤：

1. 输入图像$I_0$，通过前向传播，得到predicted score $f_c\left(I_0\right)$。
2. 利用CNN的链式求导法则（chain rule）进行反向传播，得到$f_c\left(I\right)$关于输入$I_0$的偏导数$A_c$，$A_c$即为论文中的attention map。

4.2 Attention Regularization（对应总体步骤3）

对于每一个输入的样本$I_0$，论文都会计算两种attention map：$A_p$和$A_n$，其中$A_p$是positive attention map，$A_n$是negative attention map。根据公式(2)，我们有：
$$\{\begin{array}{c}{A}_p={\frac{\partial f_p\left(I\right)}{\partial I}|}_{I=I_0}\\ A_n={\frac{\partial f_n\left(I\right)}{\partial I}|}_{I=I_0}\end{array}\text{\hspace{1em}(3)}$$

公式(3)对应的代码位于官方源码run_tracker.py文件的train函数中，如下所示：

...
posguided_grads=forwordgradients(model,batch_posimgids,batch_possamples,GBP,[0,10])
sumposguided_grads= torch.sum(torch.abs(posguided_grads) ** 2, 1)
...
negguided_grads=forwordgradients(model,batch_negimgids,batch_negsamples,GBP,[10,0])
sumnegguided_grads=torch.sum(torch.abs(negguided_grads) ** 2, 1)
...

对于正的训练样本，我们期望$A_p$中对应目标物体的元素值尽可能大，反过来对于负的训练样本，我们期望$A_n$中对应目标物体的元素值尽可能小。由此，给定一个正样本（分类标签为$y=1$），论文的attention regularization可以表示为：
$$R_{\left(y=1\right)}=\frac{{\sigma }_{A_p}}{{\mu }_{A_p}}+\frac{{\mu }_{A_n}}{{\sigma }_{A_n}}\text{\hspace{1em}(4)}$$
其中，$\mu$表示均值，$\sigma$表示标准差，$\frac{{\sigma }_{A_p}}{{\mu }_{A_p}}$表示positive attention map $A_p$的变异系数（coefficient of variation，CV），它反映的是数据的离散度，数值越高则离散度越大。对于上述公式(3)，我们希望$A_p$拥有较低的离散度，而期望$A_n$拥有较高的离散度。同理，给定一个负的训练样本，其attention regularization为：
$$R_{\left(y=0\right)}=\frac{{\mu }_{A_p}}{{\sigma }_{A_p}}+\frac{{\sigma }_{A_n}}{{\mu }_{A_n}}\text{\hspace{1em}(5)}$$

关于上述两类均值和方差，论文源码的train函数中用了8个变量来表示，分别为posgradmean, posgraddelta, posgradmean_1, posgraddelta_1和neggradmean, neggraddelta, neggradmean_1, neggraddelta_1，这么做的原因是：两个式子的${\mu }_{A_p}$是不一样的，它们的${\sigma }_{A_p}$也是不一样的（$A_n$同理），如下所示：

...
posgradmean=torch.nn.functional.avg_pool2d(sumposguided_grads,[sumposguided_grads.size(1),sumposguided_grads.size(2)])
posgraddelta=(sumposguided_grads-posgradmean)**2
posgraddelta=torch.sqrt(torch.nn.functional.avg_pool2d(posgraddelta,[posgraddelta.size(1),posgraddelta.size(2)]))
...
posgradmean_1 = torch.nn.functional.avg_pool2d(sumposguided_grads_1, [sumposguided_grads_1.size(1), sumposguided_grads_1.size(2)])
posgraddelta_1 = (sumposguided_grads_1 - posgradmean_1) ** 2
posgraddelta_1 = torch.sqrt(torch.nn.functional.avg_pool2d(posgraddelta_1, [posgraddelta_1.size(1), posgraddelta_1.size(2)]))
...

综合上述公式(4)和公式(5)，论文给出了融合了attention正则项的损失函数：
$$\mathcal{L}={\mathcal{L}}_{CE}+\lambda \cdot \left[y\cdot R_{\left(y=1\right)}+\left(1-y\right)\cdot R_{\left(y=0\right)}\right]\text{\hspace{1em}(6)}$$
其中，$\lambda$是平衡因子，用于平衡交叉熵损失（cross entropy loss）${\mathcal{L}}_{CE}$和正则项。损失函数对应的代码位于官方源码run_tracker.py文件的train函数中，如下所示：

...
loss = criterion(pos_score, neg_score)
...
spaloss=(1e10*posgraddelta.sum())/(1e10*posgradmean.sum())+(1e10*neggraddelta.sum())/(1e10*neggradmean.sum())\
       +(1e10*posgradmean_1.sum())/(1e10*posgraddelta_1.sum())+(1e10*neggradmean_1.sum())/(1e10*neggraddelta_1.sum())
...
thelamb=5
finalloss=thelamb*spaloss+loss
...

4.3 Reciprocative Learning（对应总体步骤3）

关于这部分，论文给出的概念是往复学习（reciprocative learning），其具体实现为常见的CNN网络反向传播技术，当然，训练的损失函数为4.2节中改造后的损失函数。

在reciprocative learning的迭代过程中，网络会利用训练图像来计算attention map。由于在损失函数中引入了attention regularization，因此理想情况下，分类器会更加关注视频画面中的目标区域。论文以Car4视频为例，比较了with reciprocative learning与without reciprocative learning的不同效果，如下图所示：

从上图可以看出，论文利用reciprocative learning方法，在网络的迭代训练过程中其attention map逐渐覆盖目标的整个区域。Reciprocative learning对应的代码位于官方源码run_tracker.py文件的train函数中，如下所示：

...
finalloss.backward()
...

4.4 Tracking过程（对应总体步骤1 - 4）

论文的tracking过程主要分为模型初始化、在线检测（testing）和模型更新部分。

(1) 模型初始化

在第一帧中，在目标周围采集$N_1=5500$个样本（包含了正样本和负样本，其判别指标为IoU是否达到0.5），迭代次数为$H_1=50$，针对每一个样本的每一次迭代，都使用公式(6)中的损失函数进行training。

(2) 在线检测（testing）

当视频来了新的一帧，在前一帧确定的位置周围采集$N_2=256$个候选样本，然后将它们输入到CNN网络中进行正向传播（注： 论文的正向传播是没有利用正则项的），得到各自候选样本的得分，具有最大得分的候选样本位置即认为是目标在当前帧中的位置。

(3) 模型更新

继续前面在线检测的步骤，由于论文已经采集了$N_2=256$个候选样本，也得出了目标在当前帧中的位置，因此可以利用这些信息为这$N_2=256$个候选样本进行分类（利用IoU指标分出正样本和负样本），此时设置迭代次数为$H_2=15$，继续使用公式(6)对CNN网络进行training。这里需要注意：模型更新过程并非每一帧都进行，论文设定的是每隔$T=10$帧进行一次training。

论文分析了reciprocative learning方法对跟踪结果的影响，如下图所示：

上图中，绿色矩形框表示ground-truth，红色矩形框表示算法估计的位置。从图中可以看出，采用了reciprocative learning方法后，跟踪器能够在干扰场景下生成更精确的response map。

5. 总结

本文通过将attention机制整合到深度网络的损失函数中，利用reciprocative learning方法进行网络的端到端训练，为基于attention的跟踪算法中开辟了一种新的思路，并且最终取得了良好的效果。