深度强化学习研究笔记（1）——入门（马尔科夫决策过程，贝尔曼方程，价值迭代和策略迭代）

1. 强化学习（Reinforcement learning）概述

强化学习（Reinforcement learning）的基本内涵是将问题用代理（Agent，有的地方也将其翻译为智能体）和环境进行建模。其中代理能够对环境执行一些特定的动作$a\in A$，从而到达某个状态$s\in S$，然后我们就可以根据该状态为代理赋予特定的奖励$r$。强化学习的基本思想如下图所示：

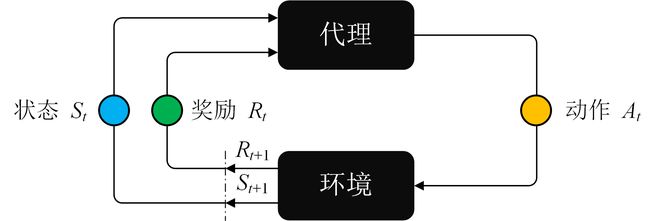
代理的目标是最大化未来的奖励总和，它通过将未来可获得的最大奖励添加到当前的奖励来实现这一点（类似于贪心算法），从而通过潜在的奖励影响当前行动（e.g., 假设知晓未来好好读书就能考上好大学从而使个人将来发展更加顺利，那么从高一开始就会好好学习）。这个潜在奖励（Value）是从当前状态开始的所有未来动作的奖励期望值的加权和。

通常人们用马尔科夫决策过程（Markov decision process，MDP） 来描述强化学习问题，一个基本的MDP问题可以用一个五元组$\left(S,A,P,R,\gamma \right)$来表示，各个符号的含义如下所示：

• $S$表示有限状态集。
• $A$表示有限动作集。
• $P$表示状态转移概率矩阵（e.g., 高三努力学习，从年级前100名到年级前20名的概率）。
  $P_a\left(s,s^{\prime }\right)=P\left(s_{t+1}=s^{\prime }|s_t=s,a_t=a\right)$表示在状态$s$下执行动作$a$后，从状态$s$转移到$s^{\prime }$的概率。
• $R$表示奖励（Reward）函数。$R_a\left(s,s^{\prime }\right)$表示在状态$s$下执行动作$a$后，从状态$s$转移到$s^{\prime }$，所得到的奖励。
• $\gamma$表示折扣因子，该因子主要用于平衡当前的奖励与未来的奖励，可以理解为权重。一般会把未来奖励的权重调低一点。

这样，MDP的目标就是找到一种策略$\pi (s)$，使得代理在状态$s$下能够做出对应的动作$a$，使得回报（Return）$G_t$能够达到最大：

$$\begin{array}{rl}{G}_t& =R_{t+1}+{\gamma }^1{R}_{t+1}+{\gamma }^2{R}_{t+2}+\dots \\ & =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\end{array}\text{\hspace{1em}(1)}$$

其中，$G_t$表示回报（Return），$R$表示奖励（Reward），$\gamma$表示折扣因子。

现在，我们再定义一个价值函数（Value function），其定义为回报的期望，用于表示当前状态的未来潜在价值（e.g., 小明当前的状态是考上了一所好大学，那么他未来的潜在价值应该比较高）：

$$V\left(s\right)=\mathbb{E}\left[G_t|S_t=s\right]\text{\hspace{1em}(2)}$$

这里需要注意区分三个概念：Reward（奖励），Return（回报）和Value（价值）：

• Reward（奖励）特指代理采取某一个动作之后的奖励，可以理解为短期的、即时的奖励。
• Return（回报）是各个短期奖励加权之和，可以视为长远的奖励。
• Value（价值）是上述长远奖励的期望。

当前，强化学习的有两种思路：基于策略（Policy）函数的强化学习和基于价值（Value）函数的强化学习。

• 基于价值（Value）函数的强化学习，它需要首先对价值进行估计，然后间接地去求解如何选择动作。
• 基于策略（Policy）梯度的强化学习，其基本原理是通过反馈调整策略，具体来说就是在得到正向奖励时，增加相应的动作的概率；得到负向的奖励时，降低相应动作的概率。

---

2. 贝尔曼（Bellman）方程

前面的公式(2)提及了价值（Value）是回报（Return）的期望，现在，我们对公式(2)进行展开，得：

$$\begin{array}{rl}V\left(s\right)& =\mathbb{E}\left[G_t|S_t=s\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+\dots |S_t=s\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma \left(R_{t+2}+\gamma R_{t+3}+\dots \right)|S_t=s\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma \cdot G_{t+1}|S_t=s\right]\end{array}\text{\hspace{1em}(3)}$$

这里回顾一下，$G_t$表示回报（Return）。由于$V\left(s\right)=\mathbb{E}\left[G_t|S_t=s\right]$，因此上式可以写成：

$$V\left(s\right)=\mathbb{E}\left[R_{t+1}+\gamma \cdot V\left(s_{t+1}\right)|S_t=s\right]\text{\hspace{1em}(4)}$$

上述公式(4)就是Bellman方程。从Bellman方程可以发现一个规律：当前状态的价值（Value）与两个因素有关：1) 当前的奖励（Reward）；2) 下一个迭代时刻的价值（Value）。

e.g., 假设当前的状态是考上了好大学，其价值（Value）是拥有一个高品质人生，当前的奖励（Reward）是接受高品质的高等教育，下一个迭代时刻的价值（Value）是拥有一份稳定的工作和报酬。那么高品质人生 = 接受高品质的高等教育 + 稳定的工作和报酬（即对应上述公式(4)）。

---

3. MDP（Markov decision process）问题建模

假设已知了状态转移概率矩阵$P$和奖励函数$R$，结合Bellman方程，我们有

$$\begin{array}{rl}\pi \left(s\right)& :=\arg \underset{a}{\max }\sum _{s^{\prime }}{P}_a\left(s,s^{\prime }\right)\left(R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right)\\ & :=\arg \underset{a}{\max }\underset{V\left(s\right)}{\mathbb{E}\left[R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right]}\\ & :=\arg \underset{a}{\max }V\left(s\right)\end{array}\text{\hspace{1em}(5)}$$

上述公式翻译过来就是：在状态$s$，我们的代理会以某种概率执行动作$a$，从而到达新的状态$s^{\prime }$，我们可以根据这个新的状态$s^{\prime }$计算【奖励（Reward）以及其价值（Value）】，根据Bellman方程，中括号内的部分就是当前状态$s$的价值（Value）。我们的代理需要在当前状态$s$下做出一个动作$a$，使得这个价值（Value）达到最大。

为后续方便起见，我们将上述公式的最后一行针对价值$V(s)$的展开部分独立出来，如下所示：

$$\begin{array}{rl}V\left(s\right)& :=\mathbb{E}\left[R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right]\\ & :=\sum _{s^{\prime }}{P}_a\left(s,s^{\prime }\right)\left(R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right)\end{array}\text{\hspace{1em}(6)}$$

---

4. 基于价值迭代（Value iteration）的求解方法

基于价值迭代的求解方法中，迭代过程中仅仅更新价值（Value），其迭代公式如下：

$$V_{i+1}\left(s\right):=\underset{a}{\max }\sum _{s^{\prime }}{P}_a\left(s,s^{\prime }\right)\left(R_a\left(s,s^{\prime }\right)+\gamma \cdot V_i\left(s^{\prime }\right)\right)\text{\hspace{1em}(7)}$$

基于value的迭代算法描述如下所示：

---

Initialize array $V$ arbitrary (e.g., $V\left(s\right)=0$ for all $s\in {\mathcal{S}}^{+}$ )

repeat
    $\Delta \leftarrow 0$
    for each $s\in \mathcal{S}$
        $v\leftarrow V\left(s\right)$
        $V\left(s\right)\leftarrow {\max }_a{\sum }_{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma V\left(s^{\prime }\right)\right]$
        $\Delta \leftarrow \max \left(\Delta ,\left|v-V\left(s\right)\right|\right)$
    end for
until $\Delta <\theta$ ($\theta$ is a small positive number)

output: a deterministic policy, $\pi$ , such that $\pi \left(s\right)=\arg {\max }_a{\sum }_{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma V\left(s^{\prime }\right)\right]$

---

从上述算法描述可以看出，价值迭代方法在求解时，会遍历状态集$S$中所有的状态，将其中具有最大价值的所对应的动作保留下来形成策略$\pi \left(s\right)$。

---

5. 基于策略迭代（Policy iteration）的求解方法

与基于价值迭代的求解方法不同，基于策略迭代的方法在迭代过程中要同时更新价值（Value）和策略（Policy）。通常它分为如下两个主要步骤：

1. 策略评估。 它对应公式(6)，如下所示：

$$\begin{array}{rl}V\left(s\right)& :=\mathbb{E}\left[R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right]\\ & :=\sum _{s^{\prime }}{P}_a\left(s,s^{\prime }\right)\left(R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right)\end{array}\text{\hspace{1em}(6)}$$

策略评估的内涵就是在给定的策略下，迭代更新价值（Value）直至收敛，从而得到稳定的价值函数。这么做的意义在于更好地估计当前策略的价值（Value）。

2. 策略改进。 它对应上述公式(5)，如下所示：

$$\begin{array}{rl}\pi \left(s\right)& :=\arg \underset{a}{\max }\sum _{s^{\prime }}{P}_a\left(s,s^{\prime }\right)\left(R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right)\\ & :=\arg \underset{a}{\max }\underset{V\left(s\right)}{\mathbb{E}\left[R_a\left(s,s^{\prime }\right)+\gamma \cdot V\left(s^{\prime }\right)\right]}\\ & :=\arg \underset{a}{\max }V\left(s\right)\end{array}\text{\hspace{1em}(5)}$$

在策略改进步骤中，代理利用步骤1中更新后的价值（Value）函数，更新每种状态下的策略并迭代，直到策略稳定下来。其迭代算法描述如下所示：

---

1. Initialization
   $V\left(s\right)\in \mathbb{R}\text{and}\pi \left(s\right)\in \mathcal{A}\left(s\right)$ arbitrary for all $s\in \mathcal{S}$

2. Policy evaluation
   repeat
       $\Delta \leftarrow 0$
       for each $s\in \mathcal{S}$
           $v\leftarrow V\left(s\right)$
           $V\left(s\right)\leftarrow {\sum }_{s^{\prime },r}p\left(s^{\prime },r|s,\pi \left(s\right)\right)\left[r+\gamma V\left(s^{\prime }\right)\right]$
           $\Delta \leftarrow \max \left(\Delta ,\left|v-V\left(s\right)\right|\right)$
       end for
   until $\Delta <\theta$ ($\theta$ is a small positive number)

3. Policy improvement
   $policystable\leftarrow \text{true}$
   for each $s\in \mathcal{S}$
       $a\leftarrow \pi \left(s\right)$
       $\pi \left(s\right)\leftarrow \arg {\max }_a{\sum }_{s^{\prime },r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma V\left(s^{\prime }\right)\right]$
       if $a̸=\pi \left(s\right)$ then
           $policystable\leftarrow \text{false}$
       end if
   end for
   if $policystable$, then
       stop and return $V$ and $\pi$
   else
       go to 2
   end if

---

6. 比较Value iteration和Policy iteration

• Policy iteration中的两个步骤都与policy直接关联，首先利用一个给定的policy，通过迭代方法对其进行评价，得到value function；接下来利用这个value function去不停地迭代各种policy，最终确定最佳policy。
• Value iteration则不直接与policy打交道，在这一类方法中，当value最后收敛，其实也相当于得到了最优的policy。

当然，以上两种求解方法也有一些共同点，比如两者在迭代计算过程中都依赖状态转移概率矩阵$P$和奖励（Reward）函数$R$。这里需要强调的是状态转移概率矩阵$P$，如果已知转移概率$P$也就称为获得了模型 Model，这种通过模型来获取最佳策略的方法也就称为 model-based 的方法。

然而，在现实场景下，有很多问题很难获取状态转移概率矩阵$P$，因此人们需要采用model-free的方法来找到最佳策略，e.g., Q-learning，Policy Gradient，Actor-Critic，这些方法都属于model-free方法。

---

7. 小结

本笔记简要说明了强化学习的基本原理，描述了基于贝尔曼方程的MDP问题建模以及两种主要的求解方法——价值（Value）迭代方法和策略（Policy）迭代方法，这两种方法都属于model-based方法，在现实场景下具有一定的局限性，后续笔记将逐步展开介绍一些典型的model-free方法。

---

参考资料：

1. 程序员带你一步步分析AI如何玩Flappy Bird
2. DQN 从入门到放弃3 价值函数与Bellman方程
3. 强化学习笔记(1)-概述
4. 深入浅出介绍策略梯度
5. A Beginner’s Guide to Deep Reinforcement Learning