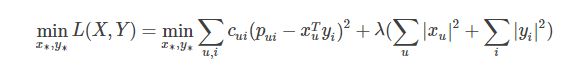Spark Mllib里的协调过滤的概念和实现步骤、LS、ALS的原理、ALS算法优化过程的推导、隐式反馈和ALS-WR算法
不多说,直接上干货!
常见的推荐算法
1、基于关系规则的推荐
2、基于内容的推荐
3、人口统计式的推荐
4、协调过滤式的推荐 (广泛采用)
协调过滤的概念
在现今的推荐技术和算法中,最被大家广泛认可和采用的就是基于协同过滤的推荐方法。
协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤 (Collaborative Filtering, 简称 CF),首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。
换句话说,就是借鉴和你相关人群的观点来进行推荐,很好理解。
协调过滤的实现步骤
要实现协同过滤的推荐算法,要进行以下三个步骤:
收集数据 ->>> 找到相似用户和物品 ->>> 进行推荐
第一步:收集数据
这里的数据指的都是用户的历史行为数据,比如用户的购买历史,关注,收藏行为,或者发表了某些评论,给某个物品打了多少分等等,这些都可以用来作为数据供推荐算法使用,服务于推荐算法。需要特别指出的在于,不同的数据准确性不同,粒度也不同,在使用时需要考虑到噪音所带来的影响。
第二步:找到相似用户和物品
这一步也很简单,其实就是计算用户间以及物品间的相似度。以下是几种计算相似度的方法:
第三步:
在知道了如何计算相似度后,就可以进行推荐了。
在协同过滤中,有两种主流方法:基于用户的协同过滤,和基于物品的协同过滤。具体怎么来阐述他们的原理呢,看个图大家就明白了。
基于用户的 CF 的基本思想相当简单,基于用户对物品的偏好找到相邻邻居用户,然后将邻居用户喜欢的推荐给当前用户。计算上,就是将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,找到 K 邻居后,根据邻居的相似度权重以及他们对物品的偏好,预测当前用户没有偏好的未涉及物品,计算得到一个排序的物品列表作为推荐。
下图给出了一个例子,对于用户 A,根据用户的历史偏好,这里只计算得到一个邻居 - 用户 C,然后将用户 C 喜欢的物品 D 推荐给用户 A。
基于物品的 CF 的原理和基于用户的 CF 类似(即基于物品的推荐和基于用户的推荐),只是在计算邻居时采用物品本身,而不是从用户的角度,即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。从计算的角度看,就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度,得到物品的相似物品后,根据用户历史的偏好预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。下图给出了一个例子,对于物品 A,根据所有用户的历史偏好,喜欢物品 A 的用户都喜欢物品 C,得出物品 A 和物品 C 比较相似,而用户 C 喜欢物品 A,那么可以推断出用户 C 可能也喜欢物品 C。
总结
以上两个方法都能很好的给出推荐,并可以达到不错的效果。
但是他们之间还是有不同之处的,而且适用性也有区别。下面进行一下对比:
计算复杂度
Item CF 和 User CF 是基于协同过滤推荐的两个最基本的算法,User CF 是很早以前就提出来了,Item CF 是从 Amazon 的论文和专利发表之后(2001 年左右)开始流行,大家都觉得 Item CF 从性能和复杂度上比 User CF 更优,其中的一个主要原因就是对于一个在线网站,用户的数量往往大大超过物品的数量,同时物品的数据相对稳定,因此计算物品的相似度不但计算量较小,同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站,对于新闻,博客或者微内容的推荐系统,情况往往是相反的,物品的数量是海量的,同时也是更新频繁的,所以单从复杂度的角度,这两个算法在不同的系统中各有优势,推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。
适用场景
在非社交网络的网站中,内容内在的联系是很重要的推荐原则,它比基于相似用户的推荐原则更加有效。比如在购书网站上,当你看一本书的时候,推荐引擎会给你推荐相关的书籍,这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到,在这种情况下,Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释,在一个非社交网络的网站中,给某个用户推荐一本书,同时给出的解释是某某和你有相似兴趣的人也看了这本书,这很难让用户信服,因为用户可能根本不认识那个人;但如果解释说是因为这本书和你以前看的某本书相似,用户可能就觉得合理而采纳了此推荐。
相反的,在现今很流行的社交网络站点中,User CF 是一个更不错的选择,User CF 加上社会网络信息,可以增加用户对推荐解释的信服程度。
LS的原理
LS是ALS算法的基础,它是一种数学优化技术,也是一种机器学习常用算法。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
LS还可以用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
ALS的原理
ALS算法是2008年以来,用的比较多的协同过滤算法。它已经集成到Spark的Mllib库中,使用起来比较方便。
从协同过滤的分类来说,ALS算法属于User-Item CF,也叫做混合CF。它同时考虑了User(用户)和Item(商品)两个方面。
用户和商品的关系,可以抽象为如下的三元组:
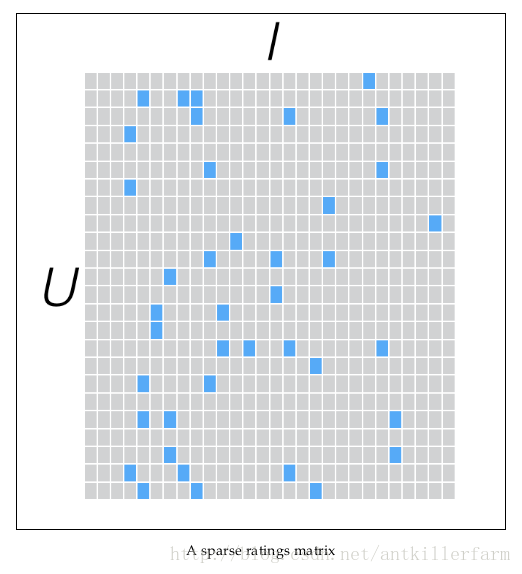
假设我们有一批用户数据,其中包含m个User和n个Item,则我们定义Rating矩阵Rm×n,其中的元素rui表示第u个User对第i个Item的评分。
在实际使用中,由于n和m的数量都十分巨大,因此R矩阵的规模很容易就会突破1亿项。这时候,传统的矩阵分解方法对于这么大的数据量已经是很难处理了。
另一方面,一个用户也不可能给所有商品评分,因此,R矩阵注定是个稀疏矩阵。矩阵中所缺失的评分,又叫做missing item。
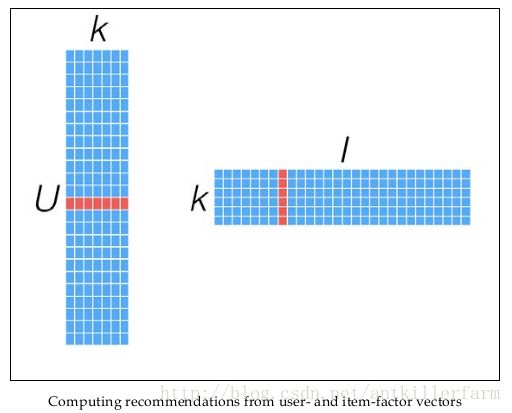
针对这样的特点,我们可以假设用户和商品之间存在若干关联维度(比如用户年龄、性别、受教育程度和商品的外观、价格等),我们只需要将R矩阵投射到这些维度上即可。这个投射的数学表示是:
这里的≈表明这个投射只是一个近似的空间变换。
其实,不懂这个空间变换的博友们,这里牵扯到奇异值分解的知识。
一般情况下,k的值远小于n和m的值,从而达到了数据降维的目的。
幸运的是,我们并不需要显式的定义这些关联维度,而只需要假定它们存在即可,因此这里的关联维度又被称为Latent factor。k的典型取值一般是20~200。
这种方法被称为概率矩阵分解算法(probabilistic matrix factorization,PMF)。ALS算法是PMF在数值计算方面的应用。
为了使低秩矩阵X和Y尽可能地逼近R,需要最小化下面的平方误差损失函数:
考虑到矩阵的稳定性问题,使用Tikhonov regularization,则上式变为:
同时,矩阵X和Y,还可以用于比较不同的User(或Item)之间的相似度,如下图所示:
ALS算法的缺点在于:
1、它是一个离线算法。
2、无法准确评估新加入的用户或商品。这个问题也被称为Cold Start问题。
ALS算法优化过程的推导
公式
的直接优化是很困难的,因为X和Y的二元导数并不容易计算,这时可以使用类似坐标下降法的算法,固定其他维度,而只优化其中一个维度。
因此整个优化迭代的过程为:
1.随机生成X、Y。(相当于对迭代算法给出一个初始解。)
Repeat until convergence {
2.固定Y,使用公式3更新xu。
3.固定X,使用公式4更新yi。
}
一般使用RMSE(root-mean-square error)评估误差是否收敛,具体到这里就是:
其中,N为三元组
因为这个迭代过程,交替优化X和Y,因此又被称作交替最小二乘算法(Alternating Least Squares,ALS)。
隐式反馈
用户给商品评分是个非常简单粗暴的用户行为。在实际的电商网站中,还有大量的用户行为,同样能够间接反映用户的喜好,比如用户的购买记录、搜索关键字,甚至是鼠标的移动。我们将这些间接用户行为称之为隐式反馈(implicit feedback),以区别于评分这样的显式反馈(explicit feedback)。
隐式反馈有以下几个特点:
1、没有负面反馈(negative feedback)。用户一般会直接忽略不喜欢的商品,而不是给予负面评价。
2、隐式反馈包含大量噪声。比如,电视机在某一时间播放某一节目,然而用户已经睡着了,或者忘了换台。
3、显式反馈表现的是用户的喜好(preference),而隐式反馈表现的是用户的信任(confidence)。比如用户最喜欢的一般是电影,但观看时间最长的却是连续剧。大米购买的比较频繁,量也大,但未必是用户最想吃的食物。
4、隐式反馈非常难以量化。
ALS-WR算法
针对隐式反馈,有ALS-WR算法(ALS with Weighted-λ-Regularization)。
首先将用户反馈分类:
但是喜好是有程度差异的,因此需要定义程度系数:
这里的rui表示原始量化值,比如观看电影的时间;
这个公式里的1表示最低信任度,α表示根据用户行为所增加的信任度。
最终,损失函数变为: