mobilenet, shufflenet 系列随笔
mobilenNet系列出自Goole,shuffleNet系列出自Face++,这两个公司的文章都是值得反复去揣摩的,去思考这些网络背后设计的出发点和设计的原则,而不是单纯停留在仅仅读懂网络结构而已。
当然本文均为笔者自身理解,读者觉得有不妥当的地方,欢迎讨论。为了方便,以下简记mobileNet为m,shuffleNet为s。
MobileNet
m v1是直筒状结构,xception使用了shortcut连接,本质上说来,我觉得xcecption更像是在向人证明depthwise结构的有效性(高于inception v3),或者说m v1在证明depthwise的高效性。m v1有一张插图是这样的,忽略最后的BN+Relu,其实就是把3*3 standard conv 拆分为3*3 depthwise+1*1 conv。此处笔者觉得不妥当,按照Fig 3,3*3 dw后面有个Relu, 用![]() 表示Relu,不可能找到权重矩阵W,W1,W2使得下面等式成立,因为左边(3*3conv)是线性的,而右边因为有
表示Relu,不可能找到权重矩阵W,W1,W2使得下面等式成立,因为左边(3*3conv)是线性的,而右边因为有![]() 所以是非线性的。所以单纯从卷积分解的角度看,dw后是不应该接Relu的。
所以是非线性的。所以单纯从卷积分解的角度看,dw后是不应该接Relu的。
![]()
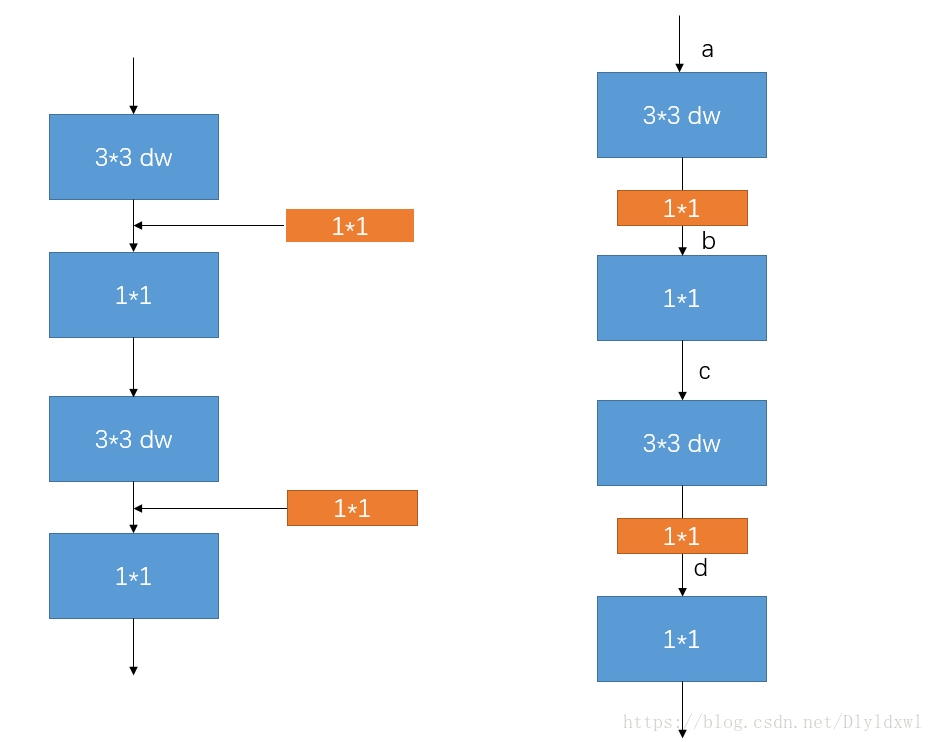
v1有什么好改的呢?怎么做到减少flops和增大acc呢?首先m v1大部分的计算量都在1*1conv上,理所当然的给1*1conv前加一个bottleneck层当然会大幅减少1*1的计算量,如下图所示。作者在v2的论文中说了,希望借助残差连接来更好的传播梯度,当然最原始的idea应该是a和c之间short cut,也就是传统的残差连接思路,bottleneck在两个胖子中间,但是此时内存利用并不高效,所以作者勉强做了一组在bottleneck之间shortcut的实验,也就是从b到d的shortcut,结果却意外的好,这时候残差连接俨然已经变成了胖子的两端是bottleneck,这和传统的看法是相反的,也就是作者说的Inverted Residuals。
论文中的t与其说是扩展比,倒不如理解为压缩比。相较于v1,bottleneck 压缩比为t,也就是说expand layer的厚度和v1差不多(参考论文会发现其channel相差不大),但是加了一些bottleneck层,导致flops下降。如果不这么理解来看的话,第一眼看肯定觉得v2用了更多dw层,也用了更多的1*1,怎么可能flops小于v1呢。.
换句话说橙色的1*1作用是bottleneck,或说筛选出重要的channel。那么有没有更廉价的方法来替代它呢?笔者抛砖引玉,提出一些思路:对于厚的map,如果再channel维度进行pooling或者说maxout,是不是也能达到降维效果呢?升维的话,考虑对现有的map进行加权来得到更多的maps呢? 如果有高效的替代1*1来完成维度的改变,那么必会带来速度的巨大提升。
在V2里面,dw后面仍然用了Relu,bottleneck后面没有接Relu。文中的解释是dw层因为维度很高,会把输入X散射的更高维的空间中,但是bottleneck却是把重要的信息保留了下来,处于一个低维的空间,Relu会破坏特征。用数学形式来表示一个3*3+Relu和dw+Relu+pw,两边都是非线性,所以说是有可能找到满足条件的权重矩阵W,W1,W2的,反而dw后不接Relu,右边就变成线性了,因此此处dw必须接Relu。
![]()
总的来说,当standard conv分解为dw+pw时,要么dw后面接一个Relu,要么pw后面接一个Relu。当dw和pw厚度一样(m v1),也即都散落在高维的特征空间中,换句话说都是处于冗余的状态,这时最好在pw后面接Relu。有必要dw后面和pw后面都加Relu吗? 笔者觉得在达到standard conv的非线性要求时,就没必要了,因为dw参数容易稀疏造成非正值,此外Relu层对于小模型来说运行也是需要时间的。当pw很瘦,dw很胖时(m v2),为了不破坏筛选出的感兴趣流形,那么就必须在冗余的dw后面加上Relu。 当然这个讨论的前提是dw是用来分解代替standard conv的。
m v2用了大量的Relu6,有利于量化,这个工作后续在讨论。
ShuffleNet
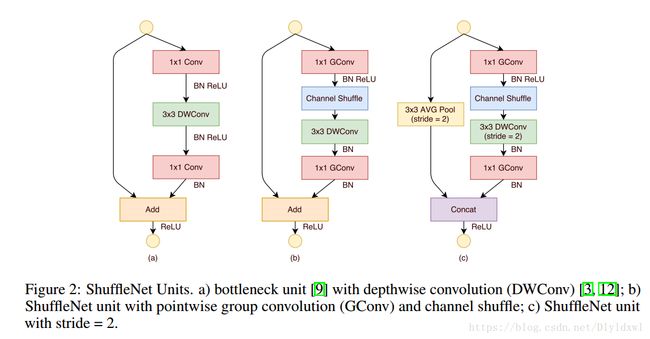
说到shufflenet,笔者觉得不得不提一下Resnext网络。Resnext在Resnet的基础上引入cardinality参数,什么意思呢?通俗的说,对残差单元的3*3层引入group参数,那么在保证同样的flops情况下,可以增大网络的厚度,提高了网络的带宽,带来了效果上得提升。作者在论文中提到cardinality越大,也即group越多,效果越好,Resnext论文中让group=32/64等。显然问题来了,这个group不能再大一点吗?这给Face++留机会了。在Residuals block中,显然group的极限显然是input channel,也就是说3*3 group conv变成了3*3 dw层。很明显此时block就是下图的(a)。关于Relu的问题,此时dw仅仅是作为cardinality的极限,并不是什么分解作用,所以理论上后面有Relu;下面的1*1没有Relu,这是沿袭了Resnet的做法,add之后再加Relu,add是线性操作,所以理论上不影响该层非线性,至于为什么在add之后加Relu而不是直接在1*1后面加,参考kaiming以前paper的对比试验。关于这个block,笔者觉得更多是一个理论性的block,也就是作者根据Resnext想出来的。
3*3变成dw后,bottleneck层也失去了bottleneck的作用,因为它的channel也变成了input channel。对于小模型来说,显然这会增大很多计算量,所以被迫引入了group参数来进行trade off between flops and acc。全部都是group卷积,必定引起channel信息流通问题,所以又引入了channel shufflle 操作,其实这就是一个np.reshape(还原到原来的groups)+np.transpose操作,但是能想到也是很厉害了,点个赞。此时结构就变成了(b),也就是shufflenet units。关于Relu的问题,dw后面没有Relu,笔者觉得这是作者试出来的结果,论文中也说了这个参考了xception。其实从宏观上看起来,3*3dw+1*1Gconv(厚度相等)也就相当于3*3的standard conv,参考m v1,当然不在dw后面接Relu了。
还有个问题就是block里面全是group conv,为什么只在第一个gconv后面添加shuffle呢?因为此时的3*3dw+1*1gconv替换的是3*3 group conv(本质上共用filter的channel维度生成同一组map,,然后加权输出),显然只需要在两个gconv中间添加shuffle即可。
ShuffleNet V2的设计笔者觉得不单单是基于v1的,还主要参考了论文中提到的四个准则,不像m v2直接基于v1顺理成章的提出了Inverted Residuals和linear bottleneck。
这四个设计原则完全是基于相同的flops,在GPU和ARM中实际运行来比较inference speed,显然这几个对比试验作者也是毫不关注acc的。笔者觉得这篇文章真的良心,有些原则以前自己也用过,但是还是缺少能力去凝练它,任重道远。
接下来看一下这四个原则。
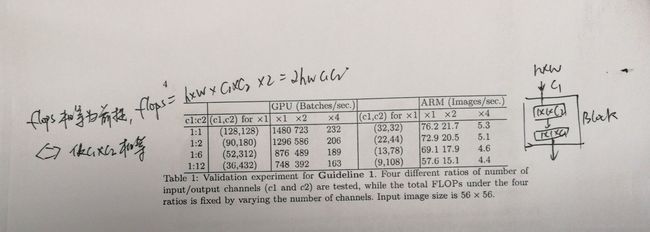
1. 输入输出channels相等最小化内存访问成本(MAC)。以1*1 conv为例,filter 为1*1*c1*c2,MAC=h*w*c1+h*w*c2+c1*c2,分别对应存储的输入/输出feature maps和卷积核,前两项可以应用基本不等式,取等条件为c1=c2,MAC最小,这些是基本的高中知识,就不推导了。作者在论文中设计了一组对比试验来验证MAC最小确能保证速度的最优,用的是两个1*1堆叠的block,repeat数次,参见下图。当然这个对比的前提是flops相等,这也是c1,c2选取的原则。
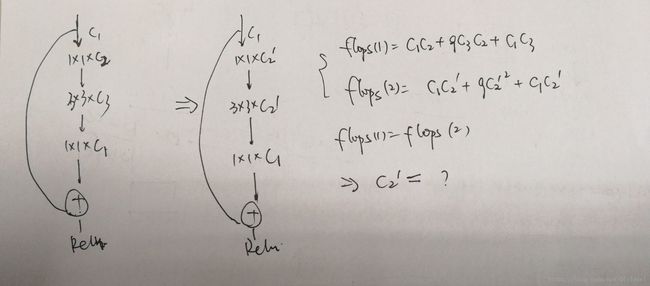
这个原则对于设计residual block时有一定的指导作用。附上我推导的一张草图,修改现行的residuals block bottleneck channel来提高速度。当然缺点也很明显,如果![]() 和
和![]() 相差较大,易导致网络特征信息传输变差,这个需要针对具体的task来权衡
相差较大,易导致网络特征信息传输变差,这个需要针对具体的task来权衡![]() 的选取。
的选取。
接下来几个原则接下里再写吧。