（论文精读）PCANet：一种简单的图像分类的深度学习基线

PCANet：一种简单的图像分类的深度学习基线

\quad\quad 这篇文章主要对论文《PCANet: A Simple Deep Learning Baseline forImage Classification?》进行中文翻译，翻译的中加入了自己的理解，如果有不恰当的地方，欢迎大家提出。
\quad\quad 论文大体可以分为五部分，摘要，引言，方法（级联线性网络结构（PCANet）,实验，结论。
论文作者;Tsung-Han Chan, Member, IEEE, Kui Jia, Shenghua Gao, Jiwen Lu, Senior Member, IEEE,
Zinan Zeng, and Yi Ma, Fellow, IEEE
论文来源：IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 24, NO. 12, DECEMBER 2015
论文链接：http://arxiv.org/abs/1404.3606
论文下载地址：https://arxiv.org/pdf/1404.3606v1.pdf

摘要

\quad\quad 在本文中，我们提出了一个非常简单的深层次基于非常的图像分类学习网络基本数据处理组件：1）级联主成分
分析（PCA）; 2）二进制散列; 3）块状直方图。在提出的架构中，PCA被用于学习多级滤波器组。接下来是简单的二进制文件用于索引和汇集的散列和块直方图。这个因此，架构称为PCA网络（PCANet）和可以非常容易和有效地设计和学习。为了比较并提供更好的理解，我们还介绍和研究了PCANet的两个简单变体：1）RandNet和2）LDANet。它们共享相同的拓扑结构PCANet，但它们的级联滤波器是随机选择的或从线性判别分析中学习。我们有广泛的在许多基准可视化数据集上测试了这些基本网络适用于不同的任务，包括野外标记面（LFW）用于面部验证; MultiPIE，扩展耶鲁B，AR，面部护理用于人脸识别的识别技术（FERET）数据集;MNIST用于手写数字识别。令人惊讶的是所有任务，这种看似天真的PCANet模型都与之相提并论最先进的功能，无论是前缀，高度手工制作，或[通过深度神经网络（DNN）]仔细学习。更令人惊讶的是，该模型为许多分类设定了新记录扩展的耶鲁B，AR和FERET数据集和关于MNIST的变化。其他公众的其他实验数据集还证明了PCANet作为个整体的潜力简单但竞争激烈的纹理分类基线和对象识别。
关键词 - 卷积神经网络，深度学习，PCA网络，随机网络，LDA网络，人脸识别，手写数字识别，对象分类。

引言

\quad\quad 基于视觉视觉语义的图像分类是非常的挑战性的任务，主要是因为通常有很大的不同照明产生的类内变异量条件，包括光照变化、不匹配不对齐、形变因素、遮挡因素等。学者们已经做出了许多努力提出各种各样的特征来应对这些变化。代表性示例是用于纹理和面部分类的Gabor特征和局部二元模式（LBP）以及用于对象识别的SIFT和HOG特征。虽然这些手选的底层特征能够很好的应对特定情况下的数据处理任务，但是这些特征的泛化能力有限，对待新问题往往需要构建新的特征。从数据中学习得到感兴趣的特征被认为是克服手选特征局限性的一个好的方法。这种方法的一个例子是通过深度神经网络（DNN）进行学习，这种网络最近引起了人们的极大关注[1]。深度学习的基本思想是通过构建多层网络，对目标进行多层表示，以期通过多层的高层次特征来表示数据的抽象语义信息，获得更好的特征鲁棒性。图像分类中深度学习成功的一个关键的框架是卷积网络框架的使用[3] - [10]。卷积深度神经网络（ConvNet）框架[3] - [5]，[8]，[9]由多个可训练的阶段组成，这些阶段彼此叠加，然后是监督分类器。每个阶段通常由“三层”组成 - 卷积层、非线性处理层以及下采样层。通常，这种网络通常使用梯度下降（SGD）方法来对其进行训练。尽管已经针对不同的视觉任务提出了许多深度卷积网络的变化，并且取得了显著成效。一个典型的例子就是小波散射模型（ScatNet），其通过将卷积核改为小波核来避免算法学习的步骤。然而就是这一简单改动，使其居然能够在手写数字识别和文本识别等方面超过相同层次的卷积网络和深度神经网络，不过由于
难以应对光照变化和遮挡影响，它在人脸识别方面表现不佳。

A动机和目的

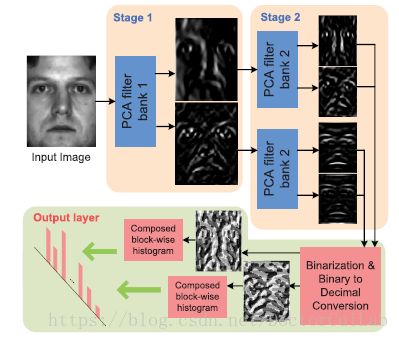
\quad\quad 我们研究的最初动机是希望解决卷积网络（ConvNet）和小波网络（ScatNet）之间的某些明显差异。我们希望实现两个简单的目标：首先，我们希望设计一个简单的深度学习网络，该网络应该非常容易，甚至是微不足道的，以便训练和适应不同的数据和任务。其次，其次，希望能为深度学习的深入研究和应用提供一个基本的参考基准。解决方案：，我们使用最基本的PCA滤波器作为卷积层滤波器，在非线性层使用二值化哈希编码处理，在重采样层使用分块扩展直方图并辅以二值哈希编码，将重采样层的输出作为整个PCANet网络最终的特征提取结果，考虑到以上的因素，我们将这种简洁的深度学习结构命名PCANet。作为示例，图1示出了两阶段PCANet如何从输入图像中提取特征。

（图1)
图1.PCANet如何从中提取特征的图示，图像通过三个最简单的处理组件：PCA过滤器，二进制散列和直方图。
PCANet模型挑战了建立深度学习网络的常识，例如ConvNet [4]，[5]，[8]和ScatNet [6]，[10]：在早期阶段没有非线性操作直到最后一个输出层（使用二进制散列和直方图）计算输出特征的PCANet。然而，正如我们将通过大量实验看到的那样，这种大幅度的简化似乎并没有破坏性能。PCANet密切相关的网络可以是两阶段导向型PCA（OPCA），它首先被提出用于音频处理[11]。与PCANet的明显区别在于OPCA不与输出层中的散列和局部直方图耦合。OPCA有着额外的噪声及形变鲁棒性，当然PCANet也吸收了OPCA这一优点，对噪声有着较好的鲁棒性。。最后我们会对PCANet进行一些扩展研究，包括通过线性判别分析来训练卷积核（LDANet）、通过随机初始化的方法来出事PCANet的卷积核（RandNet）。在这项工作中，我们对这些类型的网络与其他现有网络（如ConvNet和ScatNet）进行了广泛的实验和公平比较。我们希望我们的实验和观察能够帮助人们更好地了解这些网络。

B 所做工作

\quad\quad 虽然我们初始的目的是通过构建一个简单的深度模型框架来为大家提供一个横向深度学习模型性能的基本标准，但我们的研究结果会带来各种令人愉快但引人深思的惊喜：：这个基本的PCANet框架，在一些主流的数据库上所表现出的优越性能，例如人脸识别、手写字体分类、文本分类等等，已经能和当下相对成熟的深度学习模型相匹敌。以单样本人脸识别为例，在Yale B数据库上达到了99.58%正确率，在AR数据库的光照子集上达到了95%的识别率，在FERET数据库上达到97.25%正确率，在其DUP-1和DUP-2两个子集上分别达到95.84%和94.02%的正确率。通过实验，我们能够充分证明PCANet能够学习得到适合分类的鲁棒特征。PCANet在深度学习和视觉图像识别方面展现出了巨大价值：一方面PCANet能够充当一个简洁但又极具竞争力的深度模型判断标准；另一方面，PCANet之所以能够取得巨大成功，很大程度上得益于其分层级联的特征学习结构。更重要的是，由于PCANet在二值化哈希编码和直方图分块之后只进行一次线性映射，使其能够从数学分析判断的角度论证其有效性。、

级联线性网络结构（PCANet）

A、PCANet的网络结构

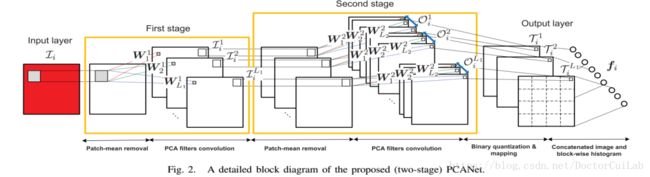
　$$(图2)$$
图2是一个典型的PCANet模型，途中只用PCA滤波器核需要从训练样本集中进行学习，我们会依据这个网络结构来详细的介绍各个部分。
输入层：PCANet选取了一个k1k2的窗口（通常选边长为3、5、7个像素正方形窗口）来滑动选取图片的局部特征。

(1)第一层（PCA）：
对于每个像素，我们都在其周围进行一次k1k2的块采样（这里采样时逐个像素进行的，因此是完全的覆盖式采样），然后收集所有的采样块，进行级联，作为第i张图片的表示

$$x_{i,1},x_{i,2},\cdots ,x_{i,\hat{m}\hat{n}}\in R^{k_1{k}_2}$$

其中： $$\hat{m}=m-[k_1/2],\hat{n}=n-[k_2/2]$$

对采样块均值化：
$$\overline{X_i}=[{\overline{x}}_{i,1},{\overline{x}}_{i,2},\cdots ，{\overline{x}}_{i,\hat{m}\hat{n}}]$$

然后对训练集中的其他图片也做相同处理，最终得到处理后的训练样本矩阵：

$$[{\bar{X}}_1,{\bar{X}}_2,\cdots ，{\bar{X}}_N]\in R^{k_1{k}_2\times N\hat{m}\hat{n}}$$

假定在第i层的滤波器数量为Li，PCA算法的目的就是通过寻找一系列的标准正交矩阵来最小化重构误差：

$$\underset{V\in k_1{k}_2\times L_1}{\min }||X-V{V}^T|{|}_F^2,s.t.V^{T}V=I_{L_1}$$
这个问题的求解就是经典的主成分分析，即矩阵X的协方差矩阵的前n个特征向量，因此对应的PCA滤波器表示如下：

$$W_l^1=ma{t}_{k_1{k}_2}(q_l(X{X}^T))\in R^{k_1\times k_2},l=1,2,3,\cdots ,L^1$$
这个方程的含义就是提取X的协方差矩阵的前L1个最大特征值对应的特征向量来组成特征映射矩阵。这些主成分中保留了这些零均值的训练样本的主要信息。

(2) 第二层（PCA）
第二层的映射过程和第一层的映射机制基本相同,将上一层提取到的特征与补零对其后的输入矩阵做卷积
$$I_i^l=I_i\ast W_l^1,i=1,2,\cdots ,N$$
其中*表示2D卷积.
在第二层同样对输入矩阵（也就是第一层的映射输出）进行块采样、级联、零均值化：
$${\bar{Y}}_i^l=[{\bar{y}}_{i,l,1},{\bar{y}}_{i,l,2},\cdots ,{\bar{y}}_{i,l,\hat{m}\hat{n}}]$$
$$Y^l=[{\bar{Y}}_1^l,{\bar{Y}}_2^l\cdots ,{\bar{Y}}_N^l]\in R^{k_1{k}_2\times N\hat{m}\hat{n}}$$
去平均值每块化为向量得到第二层的输入数据的块采样形式：

$$Y=[Y^1,Y^2,\cdots ,Y^{L_1},]\in R^{k_1{k}_2\times N\hat{m}\hat{n}}$$

同理，第二层的PCA滤波器同样通过选取协方差矩阵对应的特征向量来组成：

$$W_l^2=ma{t}_{k_1,k_2}(q_l(Y{Y}^T))\in R^{k_1\times k_2},l=1,2,\cdots ,L_2$$

由于第一层具有L1个滤波器核，一次第一层会产生L1个输出矩阵，在第二层中针对第一层输出的每一个特征举证，对应都产生L2个特征输出。最终对于每一张样本，二阶PCANet都会产生L1*L2个输出的特征矩阵：

$$O_i^l=\{I_i^l\ast W_l^2{\}}_{l=1}^{L^2}$$

可见，第一层和第二层在结构上是十分相似的，因此很容易将PCANet扩展成包含更多层的深度网络结构。

(3)输出层（哈希编码和直方图处理）
我们对第二层的每个输出矩阵都进行二值处理，得到的结果中只包含一和零，然后在对其进行二值化哈希编码，编码位数与第二层的滤波器个数相同：

$${\tau }_i^l=\sum _{l=1}^{L_2}{z}^{l-1}H(I_i^l\ast W_l^2)$$

这里的函数H（）类似于一个单位阶跃函数。
对于第一层的每个输出矩阵，将其分为B块，计算统计每个块的直方图信息，然后在将各个块的直方图特征进行级联，最终得到块扩展直方图特征：
$$f_i=[Bhist({\tau }_i^l),\cdots ,Bhist({\tau }_i^{L_1}){]}^T\in R^{(2^{L_2)L_{1}B}}$$
可根据实际情况选择是否重叠，通常人脸识别选择不重叠，而手写体、目标识别、纹理判别选择重叠。
（4）ConvNet和ScatNet的比较：PCANet与ConvNet有许多相似之处[5],PCANet去均值相当于ConvNet中的局部对比度归一化。此操作将所有3个补丁移动到以向量空间的原点为中心，以便学习的PCA过滤器可以更好地捕获数据中的主要变化。PCA可视为最简单的自动编码器,PCANet没有非线性层，试过加绝对整流层但没有效果。原因可能是量化和输出层的局部直方图已经引入了足够的足够的不变性和鲁棒性。比较实验证明的多层的结构能够更好的学习语意信息。
B.两种变化（RandNet和LDANet）
PCANet是一个非常简单的网络，只需要很少从训练数据中学习过滤器。人们可以立即想到两个相反方向的PCANet的两种可能的变化：
1.RandNet
用相同大小的随机滤波器替换每层的PCA滤波器。元素按照标准高斯分布产生的。我们称这样的网络为随机网络，简称RandNet。
2.LDANet
用于分类：多层线性判别分析。
如果学习网络的任务是分类，我们可以通过在训练数据中加入类标签信息进一步加强对学习过滤器的监督，并基于多类线性判别分析（LDA）的思想学习过滤器。我们称之为LDA.
LDA的思想是最大化类间变异性与类正交滤波器内的类内变化之和的比率.

$$\underset{V\in k_1{k}_2\times L_1}{\min }\frac{Tr(V^T\Phi V)}{Tr(V^T({\sum }_{c=1}^C{\Sigma }_c)V)},s.t.V^{T}V=I_{L_1}$$

实验

\quad\quad 来自MultiPIE数据集的各种所选主题的图像用于学习PCANet中的PCA过滤器。然后应用该训练的PCANet从MultiPIE，Extended Yale B，AR和FERET数据集中提取新对象的特征以进行面部识别。此外，LFW数据集用于进行有关面部验证的实验。表I列出了这些数据库和实验设置。

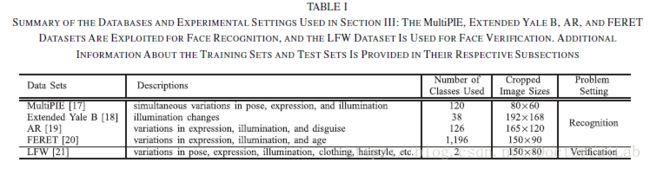
分类器：在本节中使用具有卡方或余弦距离度量的最近邻（NN）
A.（面部识别）Face Recog：MultiPIE数据集的培训和测试
首先，从MultiPIE数据集[17]组装面部训练集。选择在照明，表情和近前姿势（在正负30°内）的所有组合下的129个对象的大约100,000个图像组成通用面部训练集。使用通用面部训练集来训练PCANet，并与数据标签一起学习LDANet;然后，我们应用训练好的网络来提取MultiPIE数据集中新主题的特征。我们将所有可能的变化分为7个测试集：交叉照明，交叉表达，交叉姿势，交叉表达 加姿势，交叉照明加表达，交叉照明加姿势和交叉照明加表达和姿势。
（1）滤波器数量对交叉照明测试装置的影响：网络的滤波器大小为k1 =k2 =5，并且它们的非重叠块的大小为8 *6.对于一级网络，我们将第一级L1中的滤波器的数量从2改变为12。在考虑两级网络时，我们设置L2 =8并将L1从4变为24.结果如图3所示。

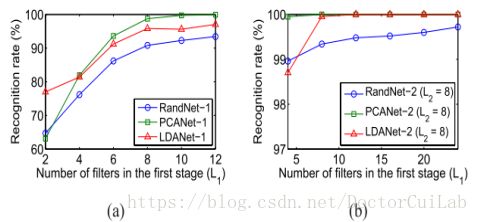
可以观察到PCANet-1实现了L1 >=4的最佳结果，并且PCANet-2提供了最佳性能对于所有正在测试的L1。此外，对于较大的L1，PCANet和LDANet（对于单级和双级网络）的准确性增加，并且RandNet也表现出类似的性能趋势。请注意，RandNet的性能平均超过10次独立运行。
（2）块大小的影响：我们接下来检查块大小（对于直方图计算）对PCANet中图像变形的鲁棒性的影响。我们使用交叉照明测试装置，并通过平移，平面内旋转和缩放将人工变形引入测试图像;参见图4.

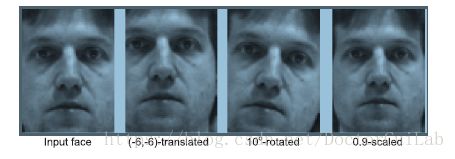
PCANet的参数设置为k1 =k2 =5和L1 =L2 =8.两个块大小，考虑了8 *6和12 *9。图5显示了每个人工变形的识别精度。 PCANet-2的精度达到90％以上，在所有方向上最多可转换4个像素，平面内旋转高达8°，刻度从0.9到1.075不等。此外，结果表明具有较大块尺寸的PCANet-2对各种变形提供了更强的鲁棒性，但是更大的块尺寸可能牺牲PCANet-1中的性能。

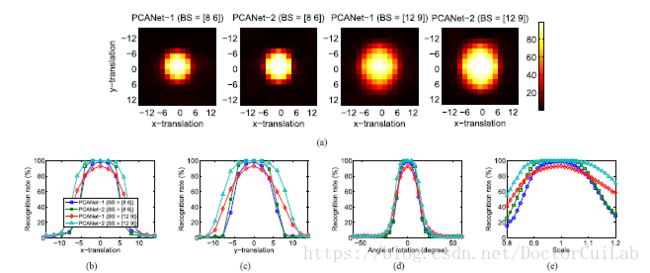
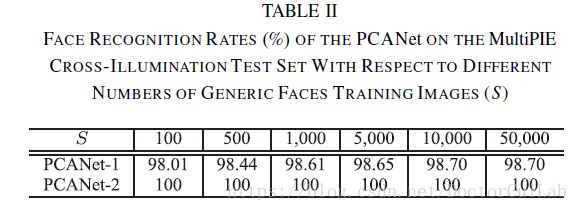
（3）通用面部数量训练样本的影响：我们还报告了针对不同数量的通用面部训练图像的PCANet的识别准确度。同样，我们使用交叉照明测试集。我们从通用面部训练集中随机选择S图像来训练PCANet并将S从100变化到50,000。 PCANet的准确性地对通用面部训练图像的数量不太敏感。随着通用面部训练样本数量的增加，PCANet-1的性能逐渐提高，即使只有100个通用面部训练样本，PCANet-2也能获得完美的识别。

B.Face Recog：扩展的耶鲁B数据集测试
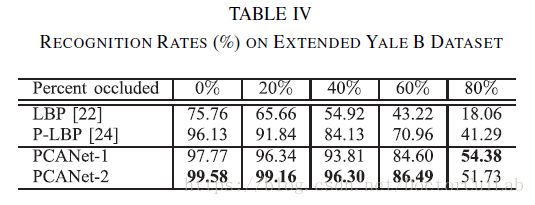
MultiPIE训练的PCANet模型应用于扩展耶鲁B数据集[18]。对于每个主题，我们选择正面照明作为图库图像，其余用于测试。在测试图像中，我们还通过用不相关的图像替换每个测试图像的随机定位的方块来模拟0到80％的各种级别的连续遮挡。示例，请参见图7。

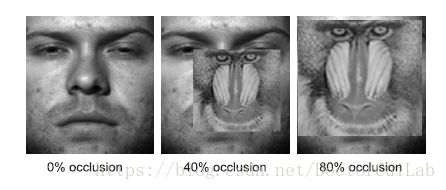
\quad\quad 实验结果在表IV中给出。可以观察到PCANet优于具有不同阻塞水平的P-LBP。此外，PCANet不仅对照明不敏感，而且对块阻塞也很强大。在这样的单人样本设置和如此困难的照明条件下，PCANet令人惊讶地实现了几乎完美的99.58％的识别率，并且当每个测试图像的60％像素被遮挡时仍然保持86.49％的准确度！在PCA过滤之后以某种方式忽略来自遮挡补丁的贡献并且不将其传递到PCANet的输出层上，从而产生对遮挡的惊人鲁棒性。

C.面部识别：在AR数据集上测试
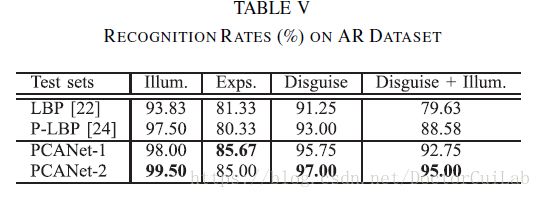
\quad\quad 在实验中，我们选择了由50名男性受试者和50名女性受试者组成的数据子集。对于每个受试者，我们在画廊训练中选择具有正面照明和神经表达的面部，其余部分用于测试。对于照明变化的测试集，PCANet的识别再次几乎是完美的，并且对于交叉伪装相关的测试集，准确度大于95％。结果与MultiPIE和Extended Yale B数据集上的结果一致：PCANet对照明不敏感并且对遮挡具有鲁棒性。

D.面部识别：在FERET数据集上测试
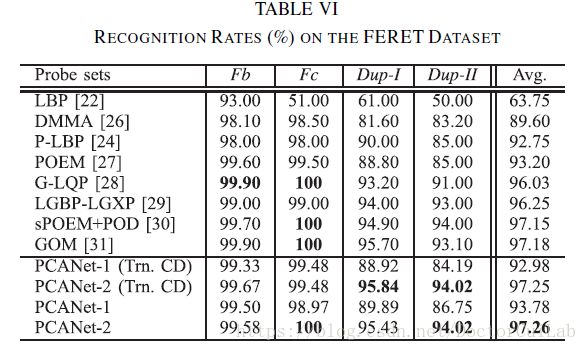
\quad\quad 将MultiPIE学习的PCANet应用FERET数据集[20]。数据集被划分为不相交的集合：gallery和probe。探针组进一步细分为四类：Fb，具有不同的表达变化; Fc，具有不同的照明条件; Dup-I，在三到四个月内拍摄;和Dup-II，相隔至少一年半。除了在MultiPIE数据库上训练的PCANet，我们还在FERET通用训练集上训练PCANet。

表VI列出了PCANet和最先进方法的结果。 MultiPIE学习的PCANet-2和FERET学习的PCANet-2（括号中的Trn.CD）分别达到了平均97.25和97.26％的最新精度。 由于MultiPIE数据集中的变化比标准FERET训练集更丰富，因此MultiPIE学习的PCANet略微优于FERET学习的PCANet，PCANet-2打破了Dup-I和Dup-II中的记录。

\quad\quad 关于人脸识别的总结评论：从上述III-A，III-B，III-C和III-D部分的实验中得出的一个重要结论是，从面部数据集中训练PCANet对于捕获面部数据集非常有效。 如果PCANet在广泛而深入的数据集上进行训练，可以进一步提高PCANet的性能并转向实际应用，这些数据集可以收集足够的类间和类内变化。
\quad\quad 实验我们就翻译到这里，其他内容直接参照原文中的数据即可。以上内容有翻译得不恰当的地方还请大家多多指正。

结论

\quad\quad 在本文中，我们提出了可以说是最简单的卷积深度学习网络-PCANet。 网络使用级联PCA，二进制散列和块直方图处理输入图像。 与大多数ConvNet模型一样，必须向PCANet提供网络参数，例如层数，过滤器大小和过滤器数量。 一旦参数得到修复，训练PCANet非常简单和有效，因为PCANet中的滤波器学习不涉及正则化参数或需要数值优化求解器。 此外，构建PCANet只包含级联线性映射，后跟非线性输出级。 这种简单性为卷积深度学习网络提供了另一种清新的视角，可以进一步促进数学分析和证明其有效性。
\quad\quad 本文中给出的广泛实验充分证明了两个事实：1）PCANet是一个非常简单的深度学习网络，可以有效地提取面部，数字和纹理图像分类的有用信息。2）PCANet可以是 研究用于大规模图像分类任务的高级深度学习架构的宝贵基线。
以上内容有翻译得不恰当的地方还请大家多多指正。

以上内容编辑：郭南南