【深度学习】BP算法-误差逆传播算法详解
前些开始准备找实习找工作了,复习机器学习算法的时候发现BP算法又忘了,这次写博客记录一下,由于我矩阵知识不是很好,所以这篇文章没有以矩阵运算的方式来讲解。本文表面是原创,实际上参考了很多很多文章
符号与神经网络结构说明
L L L : 当前神经网络的总层数
n l n^{l} nl : 第 l l l层神经元拥有的神经元个数
α i l \alpha^{l}_{i} αil : 第 l l l层神经网络中的第 i i i个神经元的输入
β i l \beta^{l}_{i} βil : 第 l l l层神经网络中的第 i i i个神经元的输出
w i j l w^{l}_{ij} wijl : 第 l l l层神经网络中的第 i i i个神经元的到第 l + 1 l+1 l+1层神经网络中的第 j j j个神经元的权重
b j l b^{l}_{j} bjl : 第 l l l层神经网络中到第 l + 1 l+1 l+1层神经网络中第 j j j个神经元的的偏置项(想不出来叫啥了)
E E E : 神经网络的总损失
f f f : 激活函数
M M M : 总样本数
x i j x_{ij} xij : 第 i i i个样本的第 j j j个属性值(特征值,whatever)
y i j y_{ij} yij : 第 i i i个样本的第 j j j个输出的真实值
y ^ i j \hat{y}_{ij} y^ij : 神经网络对于第 i i i个样本在第 j j j个输出的预测值,也就是 β j L \beta^{L}_{j} βjL
一些准备知识
神经网络内部的运算
- 神经元的输入与输出的关系: β i l = f ( α i l ) \beta^{l}_{i}=f(\alpha^{l}_{i}) βil=f(αil)
- 第 l l l层神经元与第 l + 1 l+1 l+1层神经元之间的关系: α j l + 1 = ∑ k = 1 n l w k j l β k l + b j l \alpha^{l+1}_{j}=\sum_{k=1}^{n^{l}}w^{l}_{kj}\beta^{l}_{k}+b^{l}_{j} αjl+1=∑k=1nlwkjlβkl+bjl
- 常用的均方损失: E = ∑ m = 1 M 1 2 ∑ k n L ( y m k − y ^ m k ) 2 E=\sum_{m=1}^{M}\frac{1}{2}\sum_{k}^{n^L}(y_{mk}-\hat{y}_{mk})^2 E=∑m=1M21∑knL(ymk−y^mk)2
求导的链式法则
- 如果 y = g ( x ) , z = h ( y ) y=g(x),z=h(y) y=g(x),z=h(y),那么有 ∂ z ∂ x = ∂ z ∂ y ∂ y ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x} ∂x∂z=∂y∂z∂x∂y
- 如果 y 1 = g ( x ) , y 2 = h ( x ) , z = k ( y 1 , y 2 ) y_1=g(x),y_2=h(x),z=k(y_1,y_2) y1=g(x),y2=h(x),z=k(y1,y2),那么有 ∂ z ∂ x = ∂ z ∂ y 1 ∂ y 1 ∂ x + ∂ z ∂ y 2 ∂ y 2 ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y_1}\frac{\partial y_1}{\partial x}+\frac{\partial z}{\partial y_2}\frac{\partial y_2}{\partial x} ∂x∂z=∂y1∂z∂x∂y1+∂y2∂z∂x∂y2
BP算法
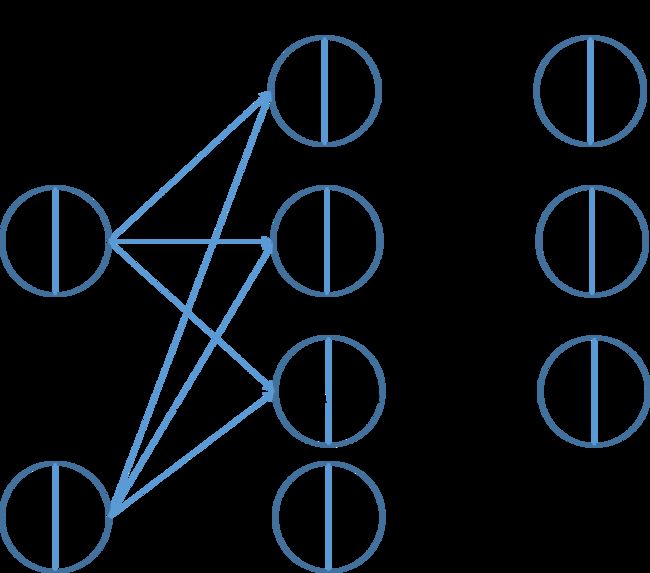
请结合图看,重点关注第 l l l层第 i i i个和第 l + 1 l+1 l+1层第 j j j个神经元之间的权重更新
由于梯度下降方法,权重一定是按下式更新的 w i j l = w i j l − η ∂ E ∂ w i j l w^{l}_{ij}=w^{l}_{ij}-\eta\frac{\partial E}{\partial w^{l}_{ij}} wijl=wijl−η∂wijl∂E因此求 ∂ E ∂ w i j l \frac{\partial E}{\partial w^{l}_{ij}} ∂wijl∂E就是BP算法的核心
由链式法则可知 ∂ E ∂ w i j l = ∂ E ∂ α j l + 1 ∂ α j l + 1 ∂ w i j l ( 1 ) \frac{\partial E}{\partial w^{l}_{ij}}=\frac{\partial E}{\partial \alpha^{l+1}_{j}} \frac{\partial \alpha^{l+1}_{j}}{\partial w^{l}_{ij}} \qquad(1) ∂wijl∂E=∂αjl+1∂E∂wijl∂αjl+1(1)
第 l l l层神经元与第 l + 1 l+1 l+1层神经元之间的关系: α j l + 1 = ∑ k = 1 n l w k j l β k l + b j l \alpha^{l+1}_{j}=\sum_{k=1}^{n^{l}}w^{l}_{kj}\beta^{l}_{k}+b^{l}_{j} αjl+1=∑k=1nlwkjlβkl+bjl可知 ∂ α j l + 1 ∂ w i j l = β i l ( 2 ) \frac{\partial \alpha^{l+1}_{j}}{\partial w^{l}_{ij}}=\beta_{i}^{l} \qquad(2) ∂wijl∂αjl+1=βil(2)
又由(2)带入(1)可得 ∂ E ∂ w i j l = ∂ E ∂ α j l + 1 β i l ( 3 ) \frac{\partial E}{\partial w^{l}_{ij}}=\frac{\partial E}{\partial \alpha^{l+1}_{j}} \beta_{i}^{l} \qquad(3) ∂wijl∂E=∂αjl+1∂Eβil(3)
由链式法则可知 ∂ E ∂ α j l + 1 = ∂ E ∂ β j l + 1 ∂ β j l + 1 ∂ α j l + 1 ( 4 ) \frac{\partial E}{\partial \alpha^{l+1}_{j}}=\frac{\partial E}{\partial \beta^{l+1}_{j}} \frac{\partial \beta^{l+1}_{j}}{\partial \alpha^{l+1}_{j}} \qquad(4) ∂αjl+1∂E=∂βjl+1∂E∂αjl+1∂βjl+1(4)
神经元的输入与输出的关系: β i l = f ( α i l ) \beta^{l}_{i}=f(\alpha^{l}_{i}) βil=f(αil)可知 ∂ β j l + 1 ∂ α j l + 1 = f ′ ( α j l + 1 ) ( 5 ) \frac{\partial \beta^{l+1}_{j}}{\partial \alpha^{l+1}_{j}}=f'(\alpha^{l+1}_{j}) \qquad(5) ∂αjl+1∂βjl+1=f′(αjl+1)(5)
由于 E E E是第 l + 2 l+2 l+2层神经元的输入 α 1 l + 2 , α 2 l + 2 , . . . , α n l + 1 l + 2 \alpha_{1}^{l+2},\alpha_{2}^{l+2},...,\alpha_{n^{l+1}}^{l+2} α1l+2,α2l+2,...,αnl+1l+2的函数,所以由链式法则第二条有 ∂ E ∂ β j l + 1 = ∑ k = 1 n l + 2 ∂ E ∂ α k l + 2 ∂ α k l + 2 ∂ β j l + 1 = ∑ k = 1 n l + 2 ∂ E ∂ α k l + 2 w j k l + 1 ( 6 ) \frac{\partial E}{\partial \beta^{l+1}_{j}}=\sum_{k=1}^{n^{l+2}}\frac{\partial E}{\partial \alpha^{l+2}_{k}} \frac{\partial \alpha^{l+2}_{k}}{\partial \beta^{l+1}_{j}}=\sum_{k=1}^{n^{l+2}}\frac{\partial E}{\partial \alpha^{l+2}_{k}} w_{jk}^{l+1} \qquad(6) ∂βjl+1∂E=k=1∑nl+2∂αkl+2∂E∂βjl+1∂αkl+2=k=1∑nl+2∂αkl+2∂Ewjkl+1(6)
将(5)(6)带入(4)可得 ∂ E ∂ α j l + 1 = f ′ ( α j l + 1 ) ∑ k = 1 n l + 2 ∂ E ∂ α k l + 2 w j k l + 1 ( 7 ) \frac{\partial E}{\partial \alpha^{l+1}_{j}}=f'(\alpha^{l+1}_{j})\sum_{k=1}^{n^{l+2}}\frac{\partial E}{\partial \alpha^{l+2}_{k}} w_{jk}^{l+1} \qquad(7) ∂αjl+1∂E=f′(αjl+1)k=1∑nl+2∂αkl+2∂Ewjkl+1(7)
到这里可以看出, w , f ′ , α j l + 1 w,f',\alpha_j^{l+1} w,f′,αjl+1都已知,如果知道了第 l + 2 l+2 l+2层的所有 ∂ E ∂ α j l + 2 \frac{\partial E}{\partial \alpha^{l+2}_{j}} ∂αjl+2∂E,就能求得第 l + 1 l+1 l+1层的所有 ∂ E ∂ α j l + 1 \frac{\partial E}{\partial \alpha^{l+1}_{j}} ∂αjl+1∂E,由(3)(7)就能得到 ∂ E ∂ w i j l = β i l f ′ ( α j l + 1 ) ∑ k = 1 n l + 2 ∂ E ∂ α k l + 2 w j k l + 1 ( 8 ) \frac{\partial E}{\partial w^{l}_{ij}}=\beta_{i}^{l} f'(\alpha^{l+1}_{j})\sum_{k=1}^{n^{l+2}}\frac{\partial E}{\partial \alpha^{l+2}_{k}} w_{jk}^{l+1} \qquad(8) ∂wijl∂E=βilf′(αjl+1)k=1∑nl+2∂αkl+2∂Ewjkl+1(8)
而对于输出层来说 ∂ E ∂ α j L = ∂ E ∂ β j L β j L ∂ α j L \frac{\partial E}{\partial \alpha^{L}_{j}}=\frac{\partial E}{\partial \beta^{L}_{j}} \frac{\beta^{L}_{j}}{\partial \alpha^{L}_{j}} ∂αjL∂E=∂βjL∂E∂αjLβjL
然后由(7)我们就可以得到上一层的 ∂ E ∂ α j L − 1 \frac{\partial E}{\partial \alpha^{L-1}_{j}} ∂αjL−1∂E,由(8)就可以的得到这一层的梯度
有了上面的基础,求 ∂ E ∂ b j l \frac{\partial E}{\partial b^{l}_{j}} ∂bjl∂E就非常简单了,因为他就等于 ∂ E ∂ b j l = ∂ E ∂ α j l + 1 ∂ α j l + 1 ∂ b j l = ∂ E ∂ α j l + 1 ∗ 1 \frac{\partial E}{\partial b^{l}_{j}}=\frac{\partial E}{\partial \alpha^{l+1}_{j}} \frac{\partial \alpha^{l+1}_{j}}{\partial b^{l}_{j}}=\frac{\partial E}{\partial \alpha^{l+1}_{j}}*1 ∂bjl∂E=∂αjl+1∂E∂bjl∂αjl+1=∂αjl+1∂E∗1
典型损失的梯度
平方损失
如果 E = ∣ ∣ y − f ( α ) ∣ ∣ 2 E=||y-f(\alpha)||^2 E=∣∣y−f(α)∣∣2,那么 ∂ E ∂ α = 2 ( y − f ( α ) ) f ′ ( α ) \frac{\partial E}{\partial \alpha}=2(y-f(\alpha))f'(\alpha) ∂α∂E=2(y−f(α))f′(α)
交叉熵损失
如果 E = − ∑ i k y i l o g f ( α i ) E=-\sum_i^k y_ilogf(\alpha_i) E=−∑ikyilogf(αi),其中 k k k为类别个数,假设该样本真实类别为 j j j,那么有 E = − l o g f ( α j ) E=- logf(\alpha_j) E=−logf(αj),于是 ∂ E ∂ α j = − f ′ ( α ) f ( α ) \frac{\partial E}{\partial \alpha_j}=-\frac{f'(\alpha)}{f(\alpha)} ∂αj∂E=−f(α)f′(α)
softmax的梯度
f ( α i ) = e α i ∑ j k e α j f(\alpha_i)=\frac{e^{\alpha_i}}{\sum_j^k e^{\alpha_j}} f(αi)=∑jkeαjeαi, f ′ ( α i ) = f ( α i ) ( 1 − f ( α i ) ) f'(\alpha_i)=f(\alpha_i)(1-f(\alpha_i)) f′(αi)=f(αi)(1−f(αi))
Resnet
resnet可以把梯度传回到更远的位置
就相当于多了个短接 E = E ( α 1 l + 2 , . . . , α 0 ) E=E(\alpha_1^{l+2},...,\alpha_0) E=E(α1l+2,...,α0),其中 α 0 = β j l + 1 \alpha_0=\beta_j^{l+1} α0=βjl+1
举个例子,一个函数 z = f ( y 1 , y 2 , y 3 ) = y 1 + y 2 + y 3 z=f(y_1,y_2,y_3)=y_1+y_2+y_3 z=f(y1,y2,y3)=y1+y2+y3,其中 y 1 = x 2 , y 2 = x 3 , y 3 = x y_1=x^2,y_2=x^3,y_3=x y1=x2,y2=x3,y3=x,那么 ∂ z ∂ x = ∂ z ∂ y 1 ∂ y 1 ∂ x + ∂ z ∂ y 2 ∂ y 2 ∂ x + ∂ z ∂ y 3 ∂ y 3 ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y_1}\frac{\partial y_1}{\partial x}+\frac{\partial z}{\partial y_2}\frac{\partial y_2}{\partial x}+\frac{\partial z}{\partial y_3}\frac{\partial y_3}{\partial x} ∂x∂z=∂y1∂z∂x∂y1+∂y2∂z∂x∂y2+∂y3∂z∂x∂y3
注意,尽管 y 3 = x y3=x y3=x, ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z和 ∂ z ∂ y 3 \frac{\partial z}{\partial y_3} ∂y3∂z也不是同一个东西奥!因为 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z还得考虑 y 1 , y 2 y_1,y_2 y1,y2

原谅我不想拿Visio画图了,看上面最简单的resnet一个案例,嘉定输入就是个一维的
求 ∂ E ∂ w 0 = ∂ E ∂ β 1 ∂ β 1 ∂ α 1 ∂ α 1 ∂ w 0 \frac{\partial E}{\partial w_0}=\frac{\partial E}{\partial \beta_1}\frac{\partial \beta_1}{\partial \alpha_1}\frac{\partial \alpha_1}{\partial w_0} ∂w0∂E=∂β1∂E∂α1∂β1∂w0∂α1,和上面不同的地方就在于 ∂ E ∂ β 1 \frac{\partial E}{\partial \beta_1} ∂β1∂E,假设短接那个变量记为 α 0 \alpha_0 α0,那么有
∂ E ∂ β 1 = ∂ E ∂ α 2 ∂ α 2 ∂ β 1 + ∂ E ∂ α 0 ∂ α 0 ∂ β 1 \frac{\partial E}{\partial \beta_1}=\frac{\partial E}{\partial \alpha_2}\frac{\partial \alpha_2}{\partial \beta1}+\frac{\partial E}{\partial \alpha_0} \frac{\partial \alpha_0}{\partial \beta1} ∂β1∂E=∂α2∂E∂β1∂α2+∂α0∂E∂β1∂α0其中 ∂ α 0 ∂ β 1 = 1 \frac{\partial \alpha_0}{\partial \beta1}=1 ∂β1∂α0=1,那么也就是说 ∂ E ∂ α 0 \frac{\partial E}{\partial \alpha_0} ∂α0∂E这个梯度被传递回去了,这样就有助于缓解梯度消失
感性认识
为什么叫反向呢?李宏毅老师给出的解释非常好,在这里简单说一下,如果我们把 ∂ E ∂ α k l + 2 \frac{\partial E}{\partial \alpha^{l+2}_{k}} ∂αkl+2∂E看做输入的话,那(8)这个式子就像这个神经网络在反着从后往前走一样,具体请见李宏毅机器学习
例子
A Step by Step Backpropagation Example