机器学习与数据挖掘第三、四周
为什么第二周没有呢……因为刚换老师,自学要适应一段时间。
本课程作者之后的学习目标是:实操代码,至少要将作者参加数学建模中用到的数据处理方法都做一遍。
首先,作者复习一下李宏毅老师的两节课程。
机器学习概述
机器学习就是让机器帮我们找一个函数!而这个函式,其实就是类神经网络!这个函式的输入可以是向量、矩阵和序列。
矩阵往往用于表示图像。
语音往往可以被表示为序列。
输出可以是数值regression、类别classification(提供给机器几个类别选项,让机器帮忙选择)、txt/image(用于机器学习的structured learning,让机器去创造事物)
其中pm2.5浓度预测就属于数值型regression的机器学习类型。
机器学习的过程
函式定义
写出一个带有未知参数的函式/模型(Model),先猜测一下f的数学式到底长什么样子。其中Model被称为机器学习的模型;![]() 被称为feature,即特征;w被称为权重,b被称为偏置。
被称为feature,即特征;w被称为权重,b被称为偏置。
这样的猜测需要一定的domain knowledge,有一定的经验。但猜测不一定是对的,需要回过头来修正这个猜测w和b。
Loss定义
定义Loss,也是一个function,输入是Model里面的参数,即L(b,w)。我们一开始给参数赋一定的初值,Loss输出的值代表当前设定的参数的值的好坏。
其中,y^真实值叫做label,e表示每次预测值与实际值的误差。L和误差e正相关,越大,表示参数越不好。这个误差可以有很多种表示法,比如差绝对值,差平方等。
代价函数有可能是一条波浪线(在二维中表示),也可以随着自变量相关因子的增多其函数也变为高维的、无法可视化展示的复杂函数。
不断测试参数的值,给出不同参数的L值的情况,上图使用色温和等高线展示了L的值,在模型选择中尽量使用Small L。越偏蓝色系,其值越小。
Optimization
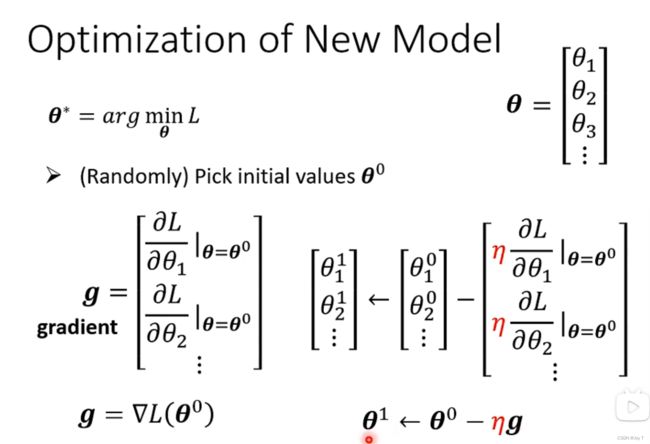
第三步本质上就是找到最好的一组w和b,使L最小。用w*,b*表示。
Gradient Descent:梯度下降方法
选取一个参数,算它与Loss值的函数:
首先要寻找一个初始点w0(最好使用特定算法使得初始值位置更优),然后计算L对w的微分是多少,根据微分正负移动w,尽量使得微分越来越接近于0。
这个移动速率取决于η,η表示学习速率,人为定义设置,能够影响w参数的移动步长,在机器学习中,人为可以设定的参数被称为hyperparameter超参数,超参数优化是我们进行的重要的步骤。
当然这个Loss可以是任何形状,取决于一开始的loss函数的定义。
当前方法有两种方式停止步进,其一是迭代次数达到一开始认为设定的某一上限,另一种表示找到导数为0的点了,但很明显如图这个不是最小的Loss点
后续改进
考虑到课程中的数据在每周具有周期性,所以x1这样的feature只能体现与前一天播放数据的关系,不如增加特征的数量为7天,这样能够更好地反映出规律,再将其增加到28天、56天,得到下面关于训练集和测试集的L值:
可以得知,在一定的范围内,Model函式的feature越多,模型的拟合预测效果越佳。但往往会出现效果停滞等情况,这是为什么呢?
其实,在上图中,Model都是y关于x的线性模型,即Linear Model,线性模型是具有局限性的,往往不可能通过一条直线很好地预测现实生活的数据关系。
如何绘制非线性的model呢?以红色model为例,它属于piecewise linear curve,即分段线性函数,每个自区间上的函数都是线性函数。它本质上只由常数和一组蓝色折线函数(Hard Sigmoid)组成。
即使是超出分段线性函数的model,也能通过插值函数进行拟合:
所以,只要我们有足够多的蓝色Function,就能组合成任何形状的函数model曲线。
如何写出蓝色的Function呢?
方法一:通过sigmoid函数逼近
sigmoid函数的形状和c/b/w取值有关,通过不断变化三者的取值来选取合适的sigmoid曲线,即:
所以想要拟合非线性函式,就把原来的b+wx1换成b+所有sigmoid函数之和!注意,上图只是考虑x1这一个feature,如果考虑多个feature,就把wx1换成相应的![]() 即可:
即可:
i表示sigmoid函数的数量,或者可以理解为标号id。
其实就是,把整个函数分成多个线性段,每个线性段通过sigmoid函数去拟合,而每个线性段都有可能和每个特征![]() 有关,所以对于每个线性段都结合权重与特征进行表示。
有关,所以对于每个线性段都结合权重与特征进行表示。
利用线性代数的知识表示成如上形式。这个r不是sigmoid函数,sigmoid需要将取负再改变一些,用a表示:
根据函式的参数得到Loss后,使用梯度下降法得到最优解。
方法二:通过ReLU函数逼近
将两条ReLU合并,就能生成一个Hard Sigmoid,也就是之前的蓝色Function,用于拟合非线性Model的。
无论是Sigmoid还是ReLU在机器学习中都属于一类函数:Activation function 激活函数。
深度神经网络
a向量是Model的参数,是众多激活函数(Sigmoid/ReLU/...)组成的。我们可以进一步改进这个a,将a作为新的输入,分配新的权值、偏置和激活函数,形成a‘。只要能优化结果,让Loss更小,那么就选取新的a'作为函式的参数,本质上就是超参数不断迭代改进的过程。不断加深网络的层数layer,就形成了深度神经网络。
这些Sigmoid或者ReLU可以被称为神经元Neuron,很多的Neuron就叫做Neuron Network。每层神经元叫做隐藏层,所有隐藏层构成了深度学习Deep Learning的基础。
梯度下降
Gradient Descent(梯度下降)是一种常用的优化算法,用于求解机器学习模型中的参数。它通过迭代的方式不断更新参数,以最小化目标函数的值。
基本步骤
1. 初始化参数:选择初始参数值作为算法的起点。
2. 计算损失函数的梯度:计算目标函数(损失函数)对于每个参数的偏导数,即参数的梯度。这可以通过反向传播算法来实现。
3. 更新参数:根据参数的梯度和学习率(步长),更新参数的值。梯度乘以学习率表示每次迭代时参数的更新量。
4. 重复迭代:重复执行步骤2和步骤3,直到满足停止条件,例如达到最大迭代次数或参数变化很小。
梯度下降的核心思想是沿着梯度的反方向更新参数,以逐步接近损失函数的最小值。
常见的梯度下降算法
此外,还有几种变体的梯度下降算法,包括批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-batch Gradient Descent):
1.批量梯度下降BGD:在每次迭代中,使用所有训练样本来计算梯度和更新参数。这种方法的计算量较大,但能够更准确地估计梯度。最原始形式。
2.随机梯度下降SGD:在每次迭代中,随机选择一个样本来计算梯度和更新参数。这种方法的计算量较小,但参数更新的方向可能更不稳定。
3.小批量梯度下降MBGD:在每次迭代中,随机选择一小部分样本(称为mini-batch)来计算梯度和更新参数。这种方法综合了批量梯度下降和随机梯度下降的优点,通常是最常用的梯度下降算法。也称为最速下降法!
每次更新一次参数叫做一次Update,每遍历一次训练集叫做一次epoch:
梯度下降是机器学习中常见的优化算法之一,广泛用于线性回归、逻辑回归、神经网络等模型的参数优化过程中。
梯度下降的痛点并不是Local Minimum(陷于局部最优解),而是步长的选择如果过大,会错过最优解。
梯度下山的优化算法
1.AdaGrad(适应性梯度算法):根据历史梯度信息动态调节学习率。经常更新的参数学习率就小一些,不经常更新的参数学习率就大一些。但是,在训练深度网络时可能会导致学习率过早和过量地减小。
2.RMSProp(均方根传递):优化动态学习率,为了解决 AdaGrad 在训练深度网络时的问题。它使用梯度的移动平均来调整学习率,有助于防止学习率单调下降。
3.AdaDelta:不需要设置学习率,这有助于限制累积的历史信息量。
4.Adam(自适应矩估计)算法目前最适合优化,结合了 Momentum模拟动量和RMSProp,第一阶段估计了梯度的均值,第二阶段估计了梯度的无偏方差,有助于自适应地调整学习率。
5.Momentum(动量):模拟物体运动时的惯性,使梯度下降过程更快、更稳定。