LeetCode 39. 组合总和/40. 组合总和 II

39. 组合总和

示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
分析[1]:考虑用回溯法解题。
首先将数组从小到大排序，然后从第一个数字开始遍历，若该数字不大于当前目标值，则将其加入到结果数组中，然后把目标值减去当前数字，并从当前数字开始向后递归寻找下一个满足上述条件的数字。若到某一步为止目标值为0，则将当前结果数组加入到集合中。每个数字向后遍历完之后，将其从结果数组中去除，从下一个数字开始继续寻找，直到走到数组末尾或者没有不大于目标值的数。

分析[2]:回溯法是一种选优搜索法，按选优条件向下搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
c++ code:

class Solution {
 public:
	 vector<vector<int>> res;
	 vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
	 {
		 //sort(candidates.begin(), candidates.end());//leetcode上可以忽略
		 vector<int> out;
		 helper(candidates, out, 0, 0, target);
		 return res;
	 }
	 void helper(vector<int>& candidates, vector<int>& out, int start, int Sum, int target)
	 {
		 if (Sum > target)
			 return;
		 if (Sum == target)
		 {
			 res.push_back(out);
			 return;
		 }
		 for (int i = start; i < candidates.size(); i++) 
		 {
			 out.push_back(candidates[i]);
			 Sum += candidates[i];
			 helper(candidates, out, i, Sum, target);
			 out.pop_back();
			 Sum -= candidates[i];
		 }
	 }
 };

40.组合总和 II

class Solution {
 public:
	 vector<vector<int>> res;
	 vector<vector<int>> combinationSum2(vector<int>& candidates, int target)
	 {
		 sort(candidates.begin(), candidates.end());
		 vector<int> out;
		 helper(candidates, out, 0, 0, target);
		 return res;
	 }
	 void helper(vector<int>& candidates, vector<int>& out, int start, int Sum, int target)
	 {
		 if (Sum > target)
			 return;
		 if (Sum == target)
		 {
			 res.push_back(out);
			 return;
		 }
		 for (int i = start; i < candidates.size(); i++) 
		 {
			 if(i!=start&&candidates[i-1]==candidates[i])continue;//与39题区别,
			 out.push_back(candidates[i]);
			 Sum += candidates[i];
			 helper(candidates, out, i+1, Sum, target);//与39题区别,
			 out.pop_back();
			 Sum -= candidates[i];
		 }
	 }
 };

如果用上述if(i!=start&&candidates[i-1]==candidates[i])continue;代码去掉（防止重复），则举反例：

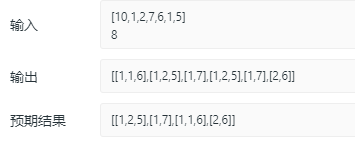
[1]https://www.cnblogs.com/wmx24/p/9015634.html
[2]https://zhangluncong.com/2018/06/03/combinationSum/
[3]https://unclegem.cn/2018/09/10/Leetcode学习笔记-39组合总和/