机器学习之k-means算法
1. K-mean聚类算法
在聚类问题中,假设训练数据
{x(1),x(2),...,x(m),}x(i)∈Rn { x ( 1 ) , x ( 2 ) , . . . , x ( m ) , } x ( i ) ∈ R n
我们想要将其分成几组聚合的”cluster”,但是没有标签y, 所以这是一个非监督的学习算法.
K-mean算法相对来说很容易理解,主要的步骤如下:
1. 随机初始化每个聚类的中心
μ1,μ2,...,μk∈Rn μ 1 , μ 2 , . . . , μ k ∈ R n
这里假设将数据分为k个类
2. 执行如下过程:
Repeat until convergence(收敛):
For every i, set
c(i):=argminj||x(i)−μj||2 c ( i ) := a r g min j | | x ( i ) − μ j | | 2
For each j, set
μj:=∑mi=1I{c(i)=j}x(i)∑mi=1I{c(i)=j} μ j := ∑ i = 1 m I { c ( i ) = j } x ( i ) ∑ i = 1 m I { c ( i ) = j }
如上, k是我们需要分类的数量, μj μ j 代表当前猜测的聚类的中心可能的值.
第1步中初始化聚类中心最简单的方式就是直接随机选择k中样本点,将它们作为初始的聚类中心,当然,其他的方式也是可以的.
第2步的循环算法包含了两步:
1. 计算每个点到聚类中心的距离,找出距离样本点最近的那个聚类,重新将该点分配到该聚类
2. 当所有样本点重新计算了所属类别之后,类内的中心点位置也相应的发生了改变,重新计算每个类簇包含的样本点的中心点
重复执行如上过程,直到中心点收敛,基本上不在发生变化或满足精度为止.
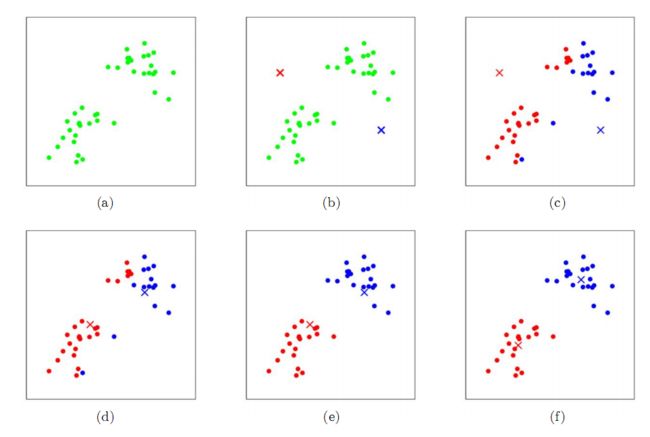
下图1.1展示了K-means算法的步骤:
- a 原始数据集
- b 随机初始化两个聚类中心(本例中没有选择样本点中的数据)
- c 计算所有样本点到聚类中心距离,将点划分到相聚最近中心点的类别
- d 重新计算聚类中心
- e 按照新的聚类中心,再次更新样本所属的类别
- f 重新计算聚类中心
到第6步之后,在继续运行下去,中心点位置也不会再改变了,所以已经收敛.
但是,K-means算法一定保证收敛吗? 让我们定义K-means的失真函数:
J(c,μ)=∑i=1m||x(i)−μc(i)||2 J ( c , μ ) = ∑ i = 1 m | | x ( i ) − μ c ( i ) | | 2
J计算的是每个样本点到自身所属类别中心点的距离之和. x(i) x ( i ) 代表样本点, μc(i) μ c ( i ) 代表第i个样本所属类别的中心点. 可以证明,K-means算法使J不断缩小.
1. 当中心点u保持不变, 更新样本点所属类别c后,因为此时每个样本点距离自己类别的中心点都是最近的,所以J是减小的.
2. 当保持样本所属类别c不变时, 更新类别的中心点u到该类别下所有样本的平均值点,此时,可以证明类内所有样本到中心点距离之和也是最小的,所以,J依然是缩小的
经过如上两个步骤不断的重复,J必定是单调递减,且必定收敛的. 通常,这也意味着c和u也是收敛的.
理论上,K-means算法有可能在几个类别间来回震荡. 例如, 几个不同的c 和/或 u, 具有相同的J, 但是在实际使用中,几乎不可能出现.
失真函数J是一个凸函数, 同时在J上使用梯度下降,并不保证一定收敛到全局最小值.通常情况下, K-means都能很好的工作,并且获得一个很好的分类效果. 但是如果你担心获取的只是局部极小值, 较常用的方法是多次随机初始化中心点,使用K-means分别进行聚类,比较最终结果,挑选最优的, 是J最小.
2. K-mean和EM算法关系
K-mean算法很简单,但是提供了一个非常有意思的求解最小值的思路,c和u就像两条腿一样,左一步右一步的逐渐获取最小值.
这个思想就是EM算法(Expectation Maximization Algorithm 最大期望算法)的核心.EM算法主要用于求解带隐含变量的概率模型的最大似然估计,分为E-步和M-步.
此处隐含变量是类别c,联合分布为
P(x,c) P ( x , c )
希望寻找到合适的类别c, 使如上联合分布概率最大.
1. E-步就是估计隐含类别c,其他参数固定, 使极大似然估计最大
2. M-步就是估计其他的参数u,使得在给定类别c的情况下,极大似然估计最大(k-means里,这一步是使失真函数J最小)
如上两步,周而复始,直至收敛,取得最大值.
EM算法的详情将在混合高斯模型中给出.
3. K-means代码实现
# --coding: utf-8 --
import sys
import matplotlib.pyplot as plt
import numpy as np
def load_train_data():
path = '../doc/soft_max_data.txt'
return np.loadtxt(path, dtype=float)[:, 0:2]
def draw_train_data(data):
plt.scatter(data[:, 0], data[:, 1])
def draw_label(data, labels, centers):
colors = ["r", "g", "y", "c"]
center_size, future_size = np.shape(centers)
sample_size = np.shape(data)[0]
for i in range(sample_size):
plt.scatter(data[i, 0], data[i, 1], marker="o", color=colors[labels[i]])
for i in range(center_size):
plt.scatter(centers[i, 0], centers[i, 1], marker="x", color="k")
def classify_label(centers, xi):
max_distance = sys.maxint
label = -1
centers_size, future_size = np.shape(centers)
for j in range(centers_size):
tmp_distance = np.sum(np.abs(xi - centers[j])) / future_size
if tmp_distance < max_distance:
max_distance = tmp_distance
label = j
return label
def get_labels(data, centers):
labels = []
sample_size = np.shape(data)[0]
for i in range(sample_size):
labels.append(classify_label(centers, data[i]))
return labels
def get_centers(data, labels):
total_count = np.zeros((4, 1))
sample_size = np.shape(data)[0]
centers = np.zeros((4, 2))
for i in range(sample_size):
label = labels[i]
centers[label] += data[i]
total_count[label] += 1
return centers / total_count
def train(train_data, centers, iter_max, precision):
labels = []
for i in range(iter_max):
labels = get_labels(train_data, centers)
tmp_centers = get_centers(train_data, labels)
changes = abs(np.sum(centers - tmp_centers))
centers = tmp_centers
if changes <= precision:
print "precision satisfied:", i
break
return centers, labels
def main():
plt.figure("mode")
train_data = load_train_data()
plt.subplot(121)
draw_train_data(train_data)
centers = np.array([[1, 2],
[50, 1],
[50, 50],
[1, 50]])
plt.subplot(122)
centers, labels = train(train_data, centers, 100, 1e-4)
draw_label(train_data, labels, centers)
plt.show()
if __name__ == '__main__':
main()
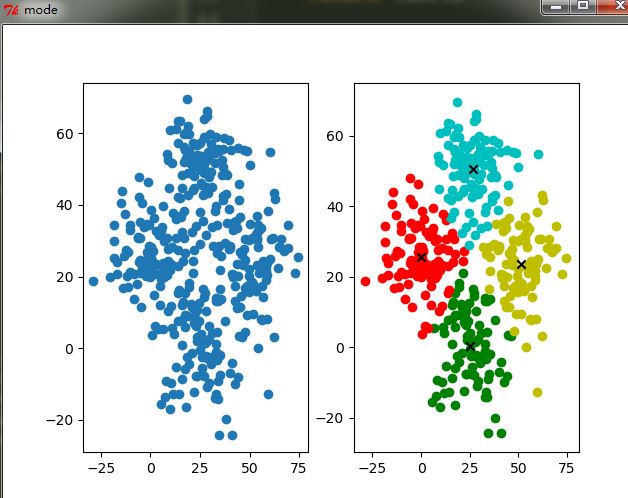
训练数据: soft_max_data.txt
结果: