狭义相对论的时空几何 --闽科夫斯基时空

前面我们讨论得到了狭义相对论的的洛伦兹变换。在此基础上介绍狭义相对论的背景时空。

一 狭义相对论的时空

简单运算就会知道狭义相对论的时空不是欧几里得时空,根据洛伦兹变换有：

t2+s2=(tx)(tx)=(sy)11−v2−−−−−√(1vv1)11−v2−−−−−√(1vv1)(sy)=1+v21−v2(s2+y2)≠s2+y2

显然在欧几里得时空中，洛伦兹变换下距离不是不变的，狭义相对论的背景时空不是欧几里得空间。

1.1 闵氏时空

根据黎曼几何，线元长度可表示为：

ds2=gijdxidxj

设G为狭义相对论空间的度规矩阵,洛伦兹变换L,以及洛伦兹变换下距离不变:

G≡(g11g21g12g22)L≡11−v2−−−−−√(1vv1)G=LGLt

可以求得G；

G≡(a00−a)

即：

ds2=a(dt2−dx2);a≠0

简单起见令 a=1

以上讨论，我们将空间局限在1维上，实际上空间是三维的，三维空间与一维时间合并在一起就是4维时空。空间分量度规应当相同，因此狭义相对论的时空的流形的度规可以表示为：

ds2=dt2−dx21−dx22−dx23

称为闽科夫斯基时空，ds称为 时空间隔。

二 世界线，时间及本征时间

狭义相对论是物理学，应当赋予时空物理意义。

2.1 事件及事件间隔

首先， (t,x1,x2,x3) 是时空中的一个点，具有唯一的时间和地点，因此代表时空中的一个事件（event）.
两点 (t0,x01,x02,x03)(t1,x11,x12,x13) 之间的”距离”，

s2=(t0−t1)2−(x01−x01)2−(x02−x12)2−(x03−x13)2

s时空间隔是两个时间之间的“距离”，在坐标变换下是不变的，这是个绝对量。

简单起见，下文仍然只讨论一维时间和一维空间。

2.2 世界线

时空中的一条曲线，代表某个质点在时空中的运动轨迹，称为世界线。世界线相交，交点代表一个相遇事件。在惯性系中，某个静止不动的质点，其速度为零，因此其运动轨迹是 t=t,x=a 在闵氏时空中是一条直线。任意一个匀速直线运动的质点，其运动轨迹是 t=t,x=vt 在闵氏时空中仍然是一条直线。在闵氏时空中惯性观者的世界线是一条直线(反之不成立，因为有直线可能是超光速的，比如同时面)。

2.3 类时曲线、固有时

当时空中的曲线，处处有速率 v(t)=dx/dt<1 时，即代表运动速度小于光速时，必有 (1−v2(t))>0 ，此时时空间隔 ds2=dt2−dx2=(1−v2(t))dt2>0 ,曲线可以求得线长： s=∫t0(1−v2(t))−−−−−−−−√dt 具有时间意义，称为曲线为类时曲线，线长称为沿该曲线运动粒子的本征时间或者固有时。

2.3.1 时钟同步

假设某个惯性观者A（做惯性运动的观察者），以这个惯性观者建立坐标系，则惯性观者的世界线为:
t=t,xi=0
考察其空间间隔：
ds2=dt2→s=∫t0dt=t 可见时空间隔代表其流逝时间，记为 tA=t 。
假设有一质点B，在惯性观者的坐标系中做惯性运动，速度为v;
则有其世界线为， vt=x ； v<1 ，这个时候必有代入时空度规有:

ds2=dt2−dx2=(1−v2)dt2→sb=∫t0(1−v2)−−−−−−−√dt=(1−v2)−−−−−−−√t

可见，在惯性观者A看来，B 点在0到t时间内，B的运动时间为t，时空间隔为 tB=(1−v2)−−−−−−−√t

B也是惯性运动，在B看来如何呢？根据洛伦兹变换有：

(sy)=11−v2−−−−−√(1−v−v1)(tx)

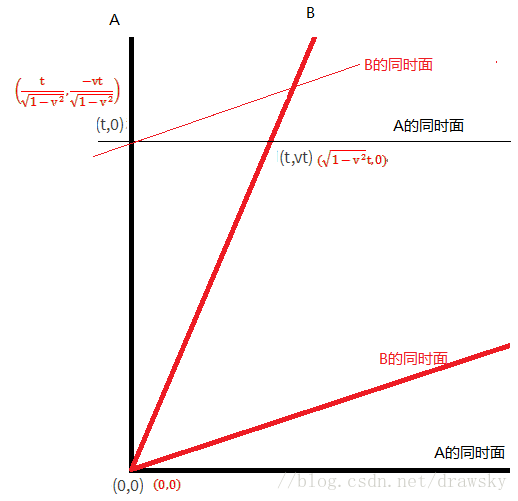
在时空中A坐标系中三个事件 e0=(0,0),e1(t,0)和e2(t,vt) ;用B的本征坐标系来看，坐标分别是：(0,0), (t1−v2√,−vt1−v2√) 和 ((1−v2)−−−−−−−√t,0)

可见，A看B在[0,t]时间内运用的时空间隔， (1−1/v2)−−−−−−−−√t 在B看来就是自己走过的时间；在B来看A的时空间隔

sA=∫t1−v2√0(1−v2)−−−−−−−√dt=t

限定上面讨论的三个事件，从上面的讨论可以看出：
1. 从固有时来看，A流逝的时间是t，B流逝的时间是 (1−v2)−−−−−−−√t ,这一结论与坐标系无关。
2. 在A看来 e1,e2 是同一时刻发生的两件事，但是自己的时间流逝了t,B的时间只流逝了 (1−1/v2)−−−−−−−−√t ，因此B 的时间走得慢；
3. 在B看来， e1 发生在 t1−v2√ 时刻,而 e2 发生在时刻 (1−v2)−−−−−−−√t ,两个事件发生的时间不相同。

不管是从哪个坐标系来看，固有时是不变的，而且相对运动的质点的走时率不一样，一个参考系认为时间同步的，另一个坐标系则时间是不同步的，走时率与时钟同步依赖于坐标系。

如下图，黑色代表A惯性系及该系下的事件坐标，红色代表B惯性系及该系下的事件坐标。

2.4 类光曲线与光子的固有时

光子的速率是1，当 v(t)=dx/dt≡1 是，曲线称为类光曲线，此时时空间隔为：

ds2=dt2−dx2=(1−v2(t))dt2≡0

光子的世界线的参数线长是0，光子固有时恒为零，光子的同时面与世界线重合并且正交。

2.5 类空曲线

当 v(t)=dx/dt>1 是，曲线称为类空曲线，此时时空间隔为：

ds2=dt2−dx2=(v2(t)−1)dx2<0

有此可得参数线长为虚数，因此对于类空曲线，我们可定义参数线长为:

l=∫x01−(dt/dx)2−−−−−−−−−−√dx

当 v(t)=dx/dt=∞ 时， δt=0→t=c ,此时 (dt/dx)=0 因此有： l=∫x01−0−−−−√dx=x
可见其物理意义类似空间距离，类空直线是某个惯性系的同时面。