排序算法

一、排序算法汇总（插入排序、交换排序、选择排序、合并排序、基数排序）

1.插入排序

    1.1直接插入排序（思想：依次将待排序序列中的每一个记录插入到一个已排好序的序列中，直到全部记录都排好序）

package edu.tcu.soft.insert;

public class DirectInsertSort {
    /*直接插入排序*/
	public int[] insertSort(int a[],int n){
		
		// a[0]作为临时一个存储单位和
		int i,j;
		for(i=2;i<=n;i++){
			a[0]=a[i];
			for(j=i-1;a[0]

    1.2希尔排序（插入排序的一种改进，思想：先将整个待排序记录序列分割成若干个子序列，在子序列内分别进行直接插入排序，待整个序列基本有序时，再对全体记录进行一次直接插入排序）

package edu.tcu.soft.insert;

public class ShellSort {
   /*希尔排序*/
	public int[] shellSort(int a[],int n){
		
		int d,i,j;
		for(d=n/2;d>=1;d=d/2){
          for(i=d+1;i<=n;i++){
        	  a[0]=a[i];
        	  for(j=i-d;j>0&&a[0]

2.交换排序

     2.1冒泡排序（思想：两两比较相邻记录的关键码，如果反序则交换，直到没有反序的记录为止）

package edu.tcu.soft.exchange;

public class BubbleSort {
	/*冒泡排序*/
    public int[] sort(int a[],int n){
    	int exchange=n;
    	while(exchange!=0){
    		int bound=exchange;
    		exchange=0;
    		for(int i=1;ia[i+1]){
    				a[0]=a[i+1];
    				a[i+1]=a[i];
    				a[i]=a[0];
    				exchange=i;
    			}
    		}
    	}
    	return a;
    }
}

     2.2快速排序（分区交换排序，思想：首先选一个轴值，将待排序记录划分成独立的两部分，左侧记录的关键码均小于或等于轴值，右侧记录的关键码均大于或等于轴值）

package edu.tcu.soft.exchange;

public class QuickSort {
	/*快速排序*/
    public void sort(int a[],int first,int end){
    	if(firsta[first])
				end--;
			if(a[end]a[end]){
				int b=a[first];
				a[first]=a[end];
				a[end]=b;
				end--;
			}
		}
		return end;
	}
}

3.选择排序

     3.1直接选择排序（第i趟排序在待排序序列r[i]~r[n](1<=i<=n-1中选取关键码最小的记录，并和第i个记录交换作为有序序列的第i个记录）

package edu.tcu.soft.select;

public class SelectSort {
	/*直接选择排序*/
    public void select(int a[],int n){
    	int i,j;
    	for(i=1;i<=n;i++){
    		int index=i;
    		for(j=i+1;j<=n;j++){
    			if(a[index]>a[j])
    				index=j;
    		}
    		if(index!=i){
    			a[0]=a[i];
    			a[i]=a[index];
    			a[index]=a[0];
    			
    		}
    	}
    }
}

     3.2堆排序（利用堆（假设利用大根堆）的特性进行排序的方法，思想：首先将待排序的记录序列构造成一个堆，此时，选出了堆中所有的记录的最大者为堆顶记录。然后将堆顶记录移走，并将剩余的记录在调整成堆，这样又找出来次大的记录）

package edu.tcu.soft.select;

public class HeapSort {
	/*堆排序*/
	public void sort(int a[], int n)//0号单元用作交换操作的暂存单元 
	{
		for (int i = n / 2; i >= 1; i--)//初始建堆，从最后一个分支节点到根节点
			sift(a, i, n); // 初始建堆
		for (int i = 1; i a[j])//根节点已经大于左右孩子中的较大者
				break;
			else {
				//将根节点与结点j交换
				a[0] = a[i];
				a[i] = a[j];
				a[j] = a[0];
				//被筛选结点位于原来结点j的位置
				i=j;
				j=2*i;
			}
		}
	}
}

4.合并排序

     4.1合并排序（归并排序，思想：将若干有序序列逐步归并，最终归并成为一个有序序列）

 package edu.tcu.soft.merge;

/**
 *    合并排序
 */
public class MergeSort {
    //1.非递归实现
	public int[] mergeSortNonRecursion(int r[],int r1[],int n){
		int h=1;//初始时子序列长度为1
		while(h

5.基数排序

     5.1基数排序

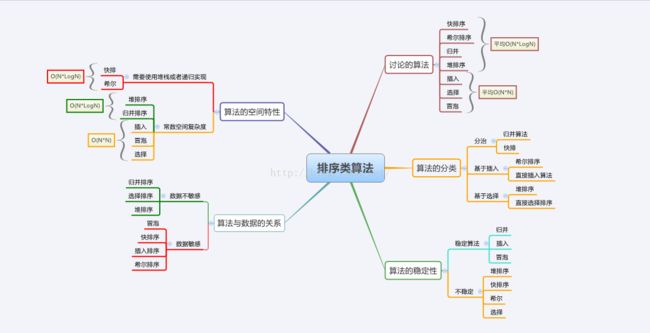
总结：

各种排序算法比较