后缀树介绍-Suffix Tree
前面的文章中有讲解了模式匹配相关的KMP和TrieTree,他们有各自的方式去提高性能,从而也应用在不同的场景中,这一次我们讲解后缀树(SuffixTree),相信如果没有专门去看过这些知识的同学应该很少知道后缀树,那么后缀树到底是什么,他能解决什么样的问题呢?
后缀树(SuffixTree)一种数据结构,通过对一个字符串所有后缀操作构建一棵树,可以支持字符串的快速匹配查询,他对于以下几个字符串问题可以做到快速实现。
1> 查找字符串A是否在字符串B中,也就是常规的字符串查找问题。
2> 计算给定的字符串A在字符串B中重复出现的次数。也就是子串重复的次数。
3> 查找字符串A的最长重复子串。
4> 查找字符串A和字符串B的最长公共子串。不是LCS问题哦!
5> 查找字符串A的最长回文子串。
6> 其实SuffixTree最常用的地方是生物学的碱基配对问题.
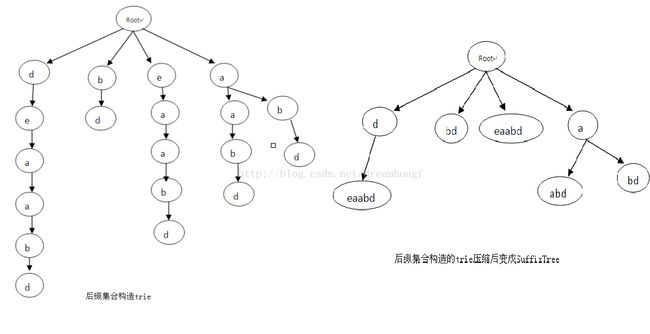
那看了上述问题,我们来讲解后缀树的结构,后缀树顾名思义是要用到字符串的后缀,先来说明下什么是后缀,比如有一个字符串dream,那么他的后缀有很多个,分别是dream它本身,ream,eam,am,m,还有一个空字符串当然也是他的后缀。他的后缀集合为:dream=suffix{dream, ream, eam, am,m,空串}。我们构建一个后缀树就要利用到这些后缀来构建一压缩的trie树,也就是Compacted Trie(将trie上单个子节点的路径进行压缩即可得到)。
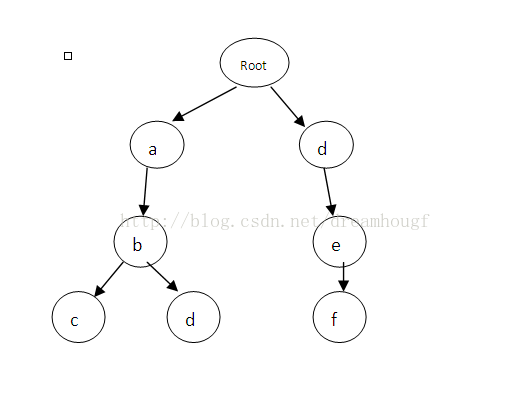
先看一个CompactedTrie的构建。假设我们的有字符串abc, abd, def我们首先用这些字符串构建一个Trie如下所示:
我们发现对于单纯的Trie每个边都是存放了一个单个字符,在空间上有些浪费,我们讲单个子节点的边都进行压缩存储在一起,如下图所示就变成了一棵压缩字典树(CompactedTrie).
后缀树(SuffixTree)其实是一棵被压缩过的TrieTree,也就是CompactedTrie,只不过后缀树中存储的关键字都是字符串的后缀,通过将一个字符串的后缀集合构造成一个TrieTree,然后在进行路径压缩,变得到了一颗后缀树,对于deaabd所实现的后缀树如下所示:
这样我们就得到了构建后缀树的抽象构造过程:首先根据文本字符串生成字符串后缀的集合;其次将每个后缀作为一个单独的关键词,构建一棵 CompactedTrie。
看到这样一棵树我们就明白后缀树到底是什么形态的了,如果你想查找某个字符串是不是子串从根节点开始按照树的结构从上到下匹配就可以了,因为如果一个字符串A是两外一个字符串B的子串,那么这个字符串A必定是字符串B的某个后缀的前缀。认识了后缀树的形态,那么很容易就会清楚后缀树的查找效率为O(m) m为需要查找的串的长度,这个速度已经相当快了,但是大家很容易就会发现,真正消耗时间的是在构建一颗后缀树,后缀树需要字符串进行预处理从而进行后缀树的构造。这也是最复杂最难的部分,主流的后缀树构造算法有两种时间复杂度,一种是构建是基于O(n^2)时间复杂度的暴力构造,当然对于时间要求和数据量小的情况这种完全也可以,另外一种是非常出名的线性时间构造也就是UKKonen的加速构造。这里我们先介绍最简单的构造方法,剩下的优化留作后面文章单独进行讲解。
暴力构造后缀树是比较简单理解也最容易实现的一种,时间复杂度是O(n^2),也就是我们上文中进行介绍的
trie—>compacted-àsuffix的方法。构造过程如下:
1> 首先求出字符串A的所有后缀,即后缀集合。
2> 使用后缀集合进行构造一棵Trie树。
3> 对trie树进行路径压缩,即得到suffix trie
下一篇文章我们讲介绍线性时间构造后缀树的方法,方法有些复杂,而且后面的文章我们还会陆续推出其他字符串模式匹配的算法,BM,AC自动机,EKMP,后缀数组等等
现在来先说明一开始讲解的SuffixTrie解决问题的方案
1. 查找字符串A是否在字符串B中,也就是常规的字符串查找问题。
用B构造后缀树,按在trie中搜索字串的方法搜索A即可。若A在B中,A肯定是B的一个后缀的前缀
2. 计算给定的字符串A在字符串B中重复出现的次数。也就是子串重复的次数。
用B+#的形式构建后缀树,查找A节点下的叶子节点的个数即为重复次数, 如果A在B中重复了3次,那么B重肯定有三个后缀的以A为前缀。
3. 查找字符串A的最长重复子串。
最深的非叶子节点所经历的字符串起来就是最长的重复子串,因为如果是重复的叶子节点必须大于1
4.查找字符串A和字符串B的最长公共子串
用A@B#作为字符串压入后缀树,找到最深的非叶子节点,并且该节点的叶子节点即有@也有#即可。最深的叶子节点是指从root所经历过的字符的个数
5.最长回文子串
我们将字符串A进行翻转得到字符串B,用字符串A和字符串B构建广义后缀树(广义后缀树传统的后缀树处理一坨单词的所有后缀。广义后缀树存储任意多个单词的所有后缀),从而最长的回文字符串就是字符串A和B的LCA(最长公共祖先)
预处理后缀树,使得查询LCA的复杂度为O(1)。这步的开销是O(N),N是单词S的长度
对单词的每一位置i(也就是从0到N-1),获取LCA(A(i), B(N-i+1)) 以及LCA(A(i+1),B(n-i+1))。查找两次的原因是我们需要考虑奇数回文和偶数回文的情况。这步要考察每坨i,所以复杂度是O(N)
找到最大的LCA,我们也就得到了回文的中心i以及回文的半径长度,自然也就得到了最长回文。总的复杂度O(n)。