当我们在聊TreeMap（一）——红黑树详解Java代码实现

本文出自：https://blog.csdn.net/DT235201314/article/details/80661157

一丶概述

上一篇讲HashMap，避开了红黑树，这边讲TreeMap，好好说一下红黑树。

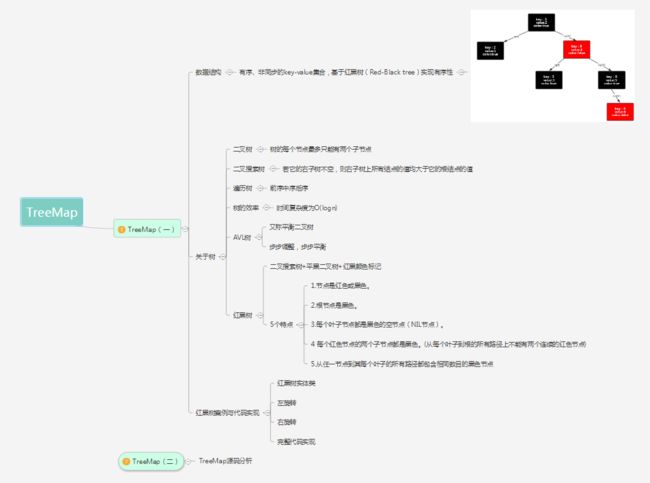
二丶概述目录图

三丶聊聊TreeMap

数据结构：

TreeMap 是一个有序、非同步的key-value集合，基于红黑树（Red-Black tree）实现有序性。

模型图：

关于树：

1、树

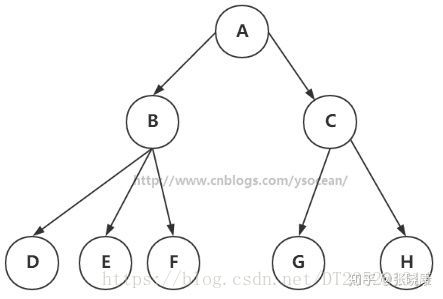
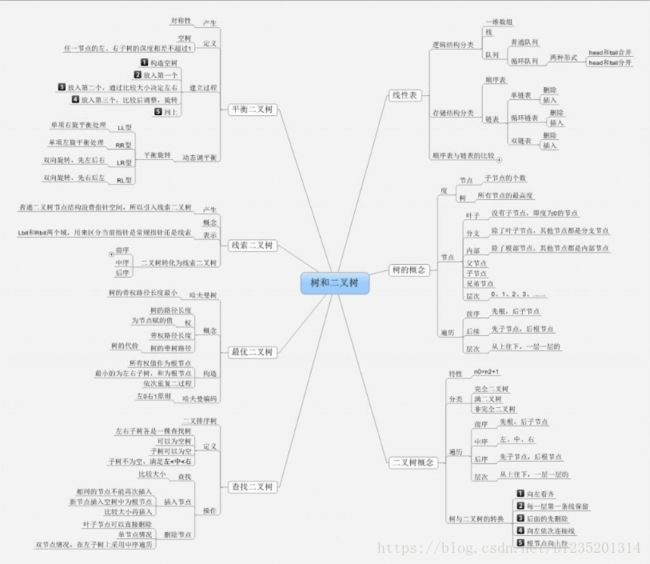
树（tree）是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

①、节点：上图的圆圈，比如A,B,C等都是表示节点。节点一般代表一些实体，在java面向对象编程中，节点一般代表对象。

②、边：连接节点的线称为边，边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在Java当中通常表示引用。

　　树有很多种，向上面的一个节点有多余两个的子节点的树，称为多路树而每个节点最多只能有两个子节点的一种形式称为二叉树。

树的常用术语

       ①、路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为“路径”。
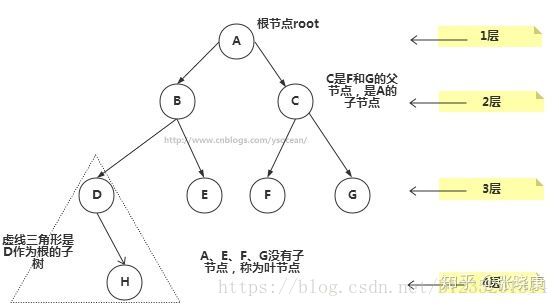
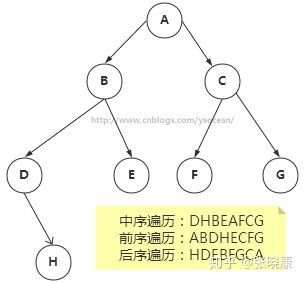
　　②、根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
　　③、父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；B是D的父节点。
　　④、子节点：一个节点含有的子树的根节点称为该节点的子节点；D是B的子节点。
　　⑤、兄弟节点：具有相同父节点的节点互称为兄弟节点；比如上图的D和E就互称为兄弟节点。
　　⑥、叶节点：没有子节点的节点称为叶节点，也叫叶子节点，比如上图的A、E、F、G都是叶子节点。
　　⑦、子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中。
　　⑧、节点的层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推。
　　⑨、深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0；

　　⑩、高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；

2、二叉树

　　二叉树：树的每个节点最多只能有两个子节点
　　上图的第一幅图B节点有DEF三个子节点，就不是二叉树，称为多路树；而第二幅图每个节点最多只有两个节点，是二叉树，并且二叉树的子节点称为“左子节点”和“右子节点”。上图的D,E分别是B的左子节点和右子节点。
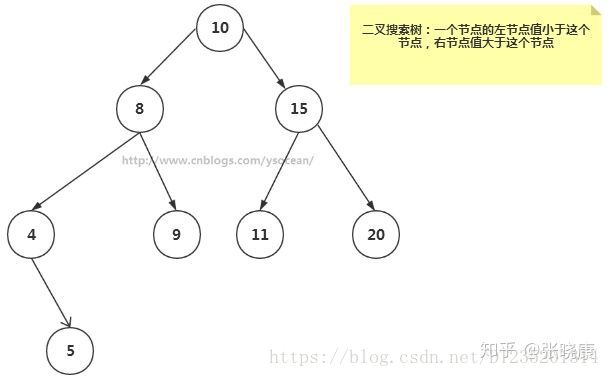
　　如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。

　　二叉搜索树要求：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

3、遍历树

　　遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历，中序遍历和后序遍历。而二叉搜索树最常用的是中序遍历。
　　①、中序遍历:左子树——》根节点——》右子树
　　②、前序遍历:根节点——》左子树——》右子树

　　③、后序遍历:左子树——》右子树——》根节点

4、树的效率

查找节点的时间取决于这个节点所在的层数，每一层最多有2n-1个节点，总共N层共有2n-1个节点，那么时间复杂度为O(logn),底数为2。

5、平衡二叉树（又称AVL树）

平衡二叉树的提出就是为了保证树不至于太倾斜(二叉搜索树弊端)，尽量保证两边平衡。因此它的定义如下：
平衡二叉树要么是一棵空树
要么保证左右子树的高度之差不大于 1
子树也必须是一颗自平衡二叉树（具有左旋转，右旋转等自平衡调整功能）

添加删除的过程中：步步调整，步步平衡

6、B树（与本文关联不大）

可参考文章：漫画：什么是B+树？

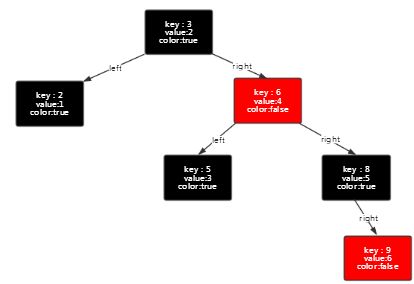
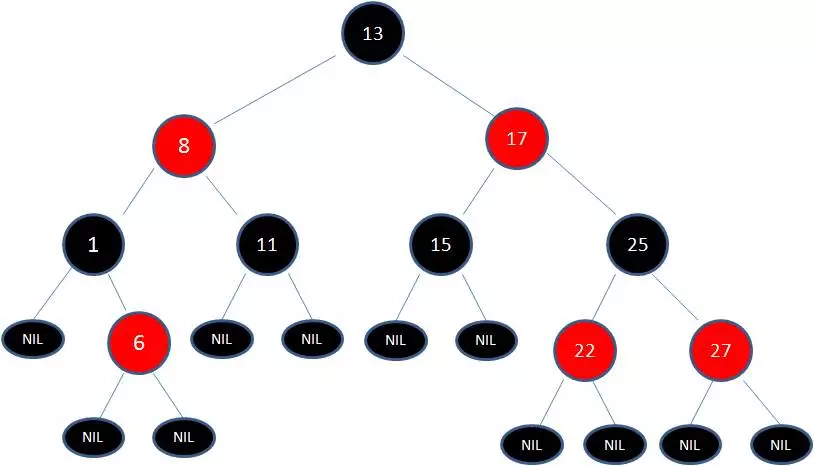
7、红黑树

红黑树是一种具有红色和黑色链接的平衡二叉查找树，同时满足：
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

红黑树实体类（Java实现）

/**
 * 
 *     author : JinBiao
 *     CSDN : http://my.csdn.net/DT235201314
 *     time   : 2018/06/13
 *     desc   :  红黑树实体类
 *     version: 1.0
 * 

 */

public class RBTreeNode<T extends Comparable<T>> {
    private T value;//node value
    private RBTreeNode<T> left;//left child pointer
    private RBTreeNode<T> right;//right child pointer
    private RBTreeNode<T> parent;//parent pointer
    private boolean red;//color is red or not red

    public RBTreeNode(){}
    public RBTreeNode(T value){this.value=value;}
    public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}

    public T getValue() {
        return value;
    }
    void setValue(T value) {
        this.value = value;
    }
    RBTreeNode<T> getLeft() {
        return left;
    }
    void setLeft(RBTreeNode<T> left) {
        this.left = left;
    }
    RBTreeNode<T> getRight() {
        return right;
    }
    void setRight(RBTreeNode<T> right) {
        this.right = right;
    }
    RBTreeNode<T> getParent() {
        return parent;
    }
    void setParent(RBTreeNode<T> parent) {
        this.parent = parent;
    }
    boolean isRed() {
        return red;
    }
    boolean isBlack(){
        return !red;
    }
    /**
     * is leaf node
     **/
    boolean isLeaf(){
        return left==null && right==null;
    }

    void setRed(boolean red) {
        this.red = red;
    }

    void makeRed(){
        red=true;
    }
    void makeBlack(){
        red=false;
    }
    @Override
    public String toString(){
        return value.toString();
    }
}

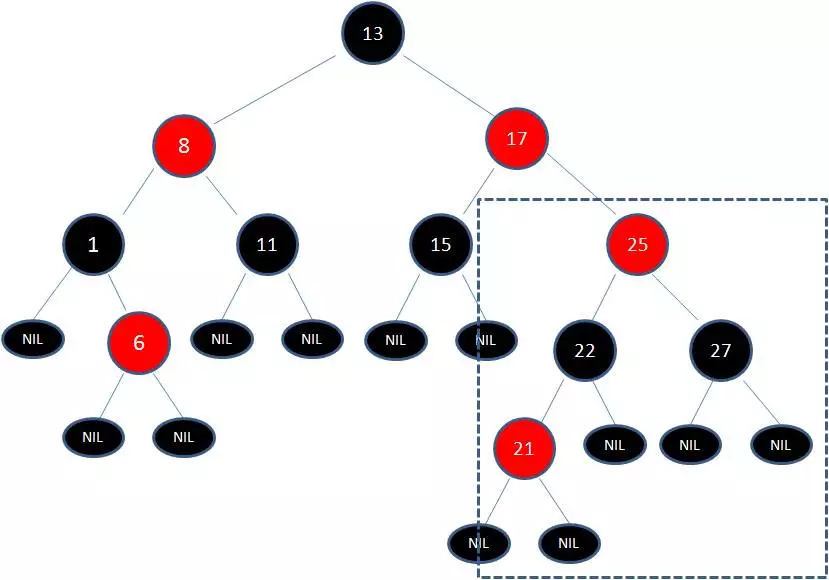
下图中这棵树，就是一颗典型的红黑树：

由于父节点15是黑色节点，因此这种情况并不会破坏红黑树的规则，无需做任何调整。
2.向原红黑树插入值为21的新节点：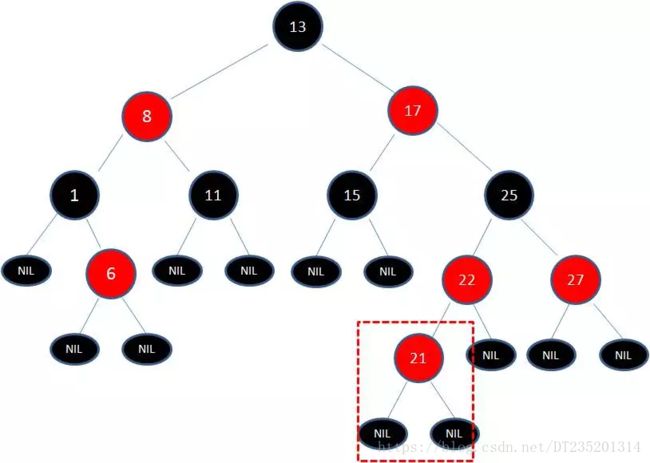

由于父节点22是红色节点，因此这种情况打破了红黑树的规则4（每个红色节点的两个子节点都是黑色），必须进行调整，使之重新符合红黑树的规则。需要通过左旋转右旋转变色来步步调整。

变色：
为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。

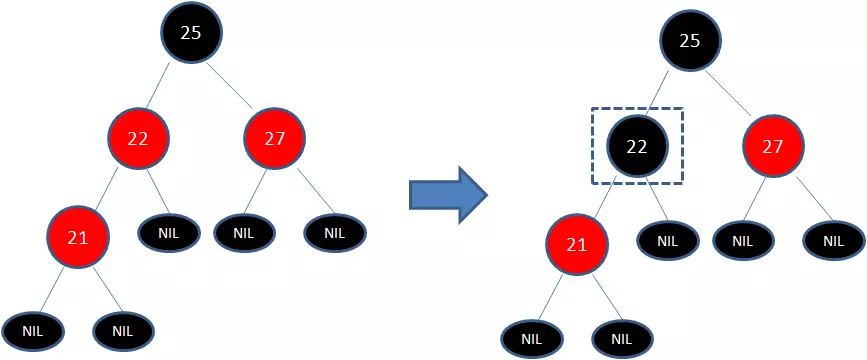
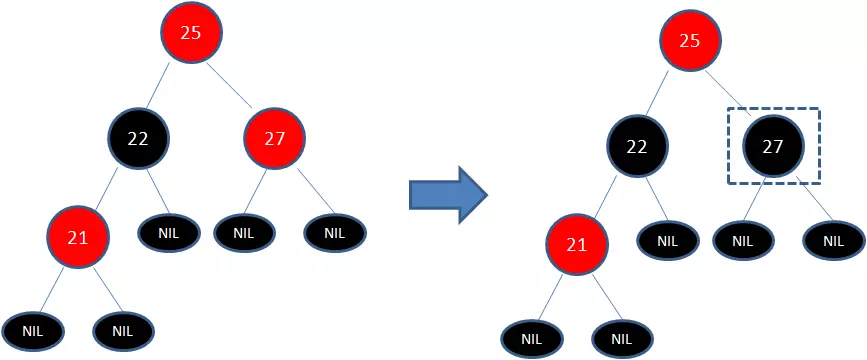
下图所表示的是红黑树的一部分，需要注意节点25并非根节点。因为节点21和节点22连续出现了红色，不符合规则4，所以把节点22从红色变成黑色：

但这样并不算完，因为凭空多出的黑色节点打破了规则5，所以发生连锁反应，需要继续把节点25从黑色变成红色：

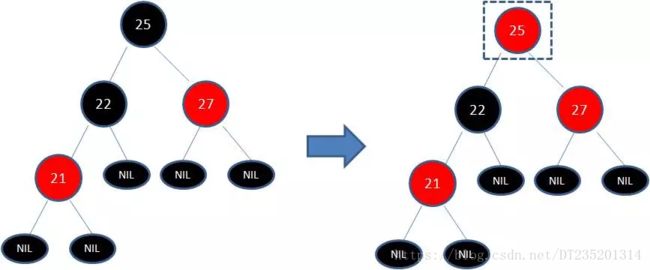
此时仍然没有结束，因为节点25和节点27又形成了两个连续的红色节点，需要继续把节点27从红色变成黑色：

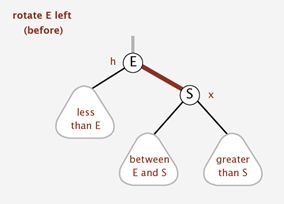
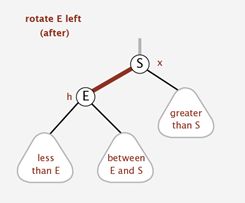
左旋转：

逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。说起来很怪异，大家看动态图：

 

代码实现：

private void rotateLeft(RBTreeNode<T> node){
    RBTreeNode<T> right = node.getRight();
    if(right==null){
        throw new IllegalStateException("right node is null");
    }
    RBTreeNode<T> parent = node.getParent();
    node.setRight(right.getLeft());
    setParent(right.getLeft(),node);

    right.setLeft(node);
    setParent(node,right);

    if(parent==null){//node pointer to root
        //right  raise to root node
        root.setLeft(right);
        setParent(right,null);
    }else{
        if(parent.getLeft()==node){
            parent.setLeft(right);
        }else{
            parent.setRight(right);
        }
        //right.setParent(parent);
        setParent(right,parent);
    }
}

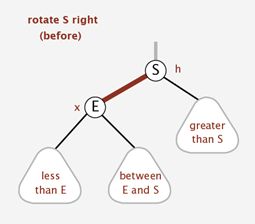
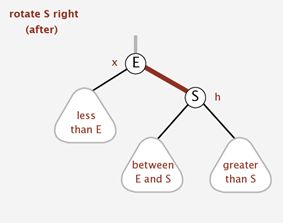
右旋转：

顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。大家看图

 

代码实现：

private void rotateRight(RBTreeNode<T> node){
    RBTreeNode<T> left = node.getLeft();
    if(left==null){
        throw new IllegalStateException("left node is null");
    }
    RBTreeNode<T> parent = node.getParent();
    node.setLeft(left.getRight());
    setParent(left.getRight(),node);

    left.setRight(node);
    setParent(node,left);

    if(parent==null){
        root.setLeft(left);
        setParent(left,null);
    }else{
        if(parent.getLeft()==node){
            parent.setLeft(left);
        }else{
            parent.setRight(left);
        }
        setParent(left,parent);
    }
}

我们以刚才插入节点21的情况为例：

首先，我们需要做的是变色，把节点25及其下方的节点变色：

此时节点17和节点25是连续的两个红色节点，那么把节点17变成黑色节点？恐怕不合适。这样一来不但打破了规则4，而且根据规则2（根节点是黑色），也不可能把节点13变成红色节点。

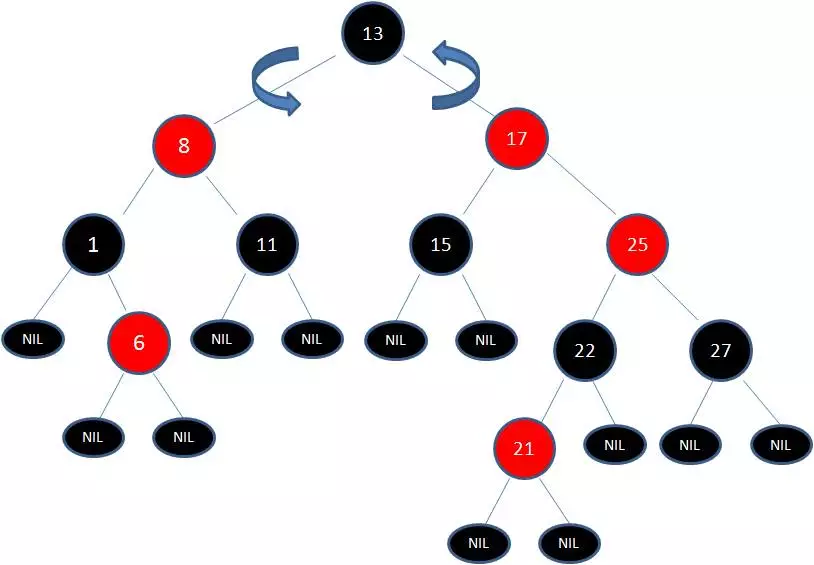
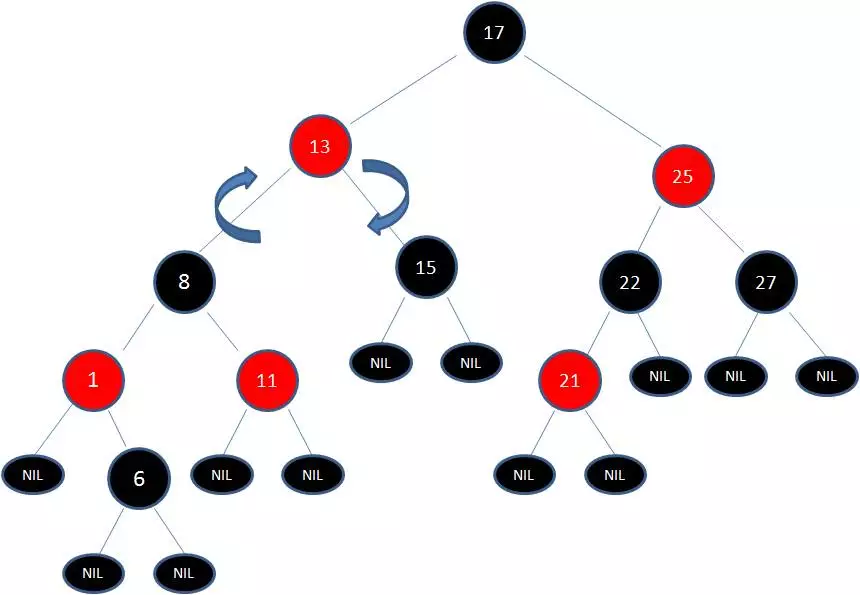
变色已无法解决问题，我们把节点13看做X，把节点17看做Y，像刚才的示意图那样进行左旋转：

由于根节点必须是黑色节点，所以需要变色，变色结果如下：

这样就结束了吗？并没有。因为其中两条路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4，其他路径的黑色节点个数是3，不符合规则5。

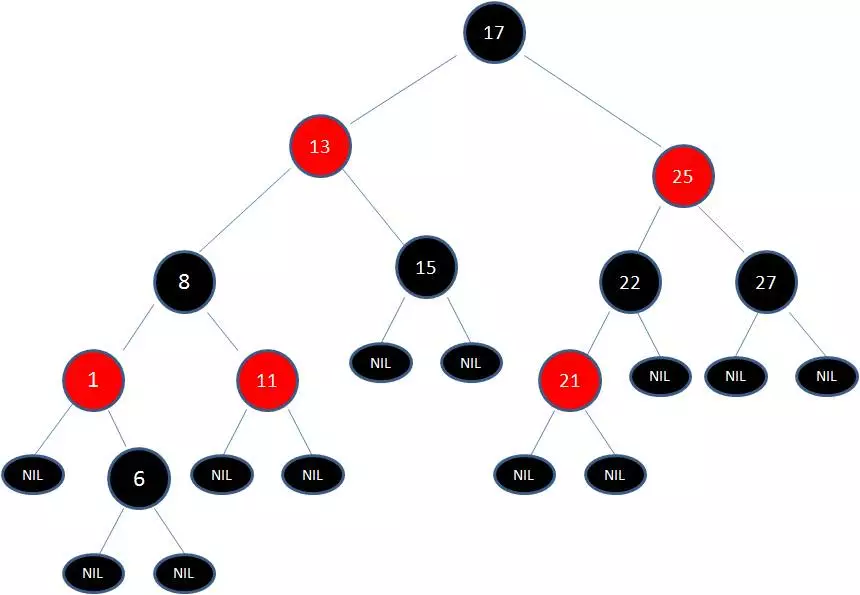
这时候我们需要把节点13看做X，节点8看做Y，像刚才的示意图那样进行右旋转：

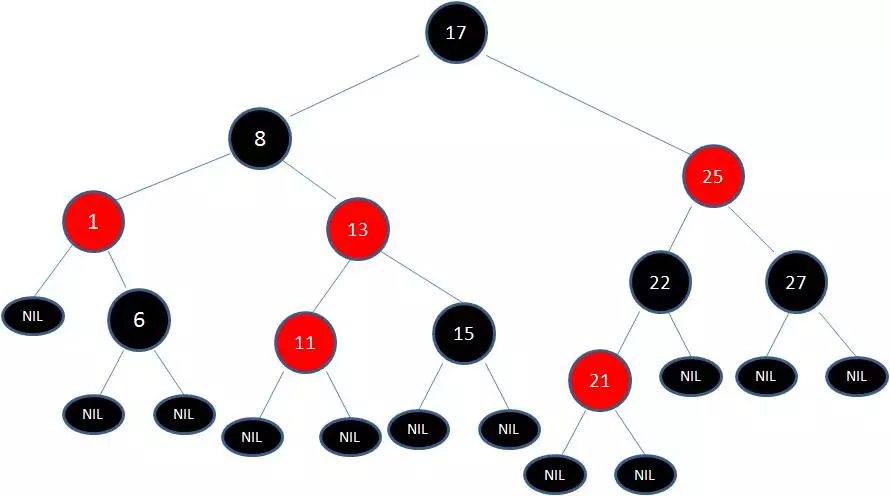
最后根据规则来进行变色：

如此一来，我们的红黑树变得重新符合规则。这一个例子的调整过程比较复杂，经历了如下步骤：

变色 -> 左旋转 -> 变色 -> 右旋转 -> 变色

红黑树实现类：

/**
 * 
 *     author : JinBiao
 *     CSDN : http://my.csdn.net/DT235201314
 *     time   : 2018/06/13
 *     desc   : 红黑树实现类
 *     version: 1.0
 * 

 */
public class RBTree<T extends Comparable<T>> {
    private final RBTreeNode<T> root;
    //node number
    private java.util.concurrent.atomic.AtomicLong size =
            new java.util.concurrent.atomic.AtomicLong(0);

    //in overwrite mode,all node's value can not  has same    value
    //in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
    private volatile boolean overrideMode = true;

    public RBTree() {
        this.root = new RBTreeNode<T>();
    }

    public RBTree(boolean overrideMode) {
        this();
        this.overrideMode = overrideMode;
    }


    public boolean isOverrideMode() {
        return overrideMode;
    }

    public void setOverrideMode(boolean overrideMode) {
        this.overrideMode = overrideMode;
    }

    /**
     * number of tree number
     *
     * @return
     */
    public long getSize() {
        return size.get();
    }

    /**
     * get the root node
     *
     * @return
     */
    private RBTreeNode<T> getRoot() {
        return root.getLeft();
    }

    /**
     * add value to a new node,if this value exist in this tree,
     * if value exist,it will return the exist value.otherwise return null
     * if override mode is true,if value exist in the tree,
     * it will override the old value in the tree
     *
     * @param value
     * @return
     */
    public T addNode(T value) {
        RBTreeNode<T> t = new RBTreeNode<T>(value);
        return addNode(t);
    }

    /**
     * find the value by give value(include key,key used for search,
     * other field is not used,@see compare method).if this value not exist return null
     *
     * @param value
     * @return
     */
    public T find(T value) {
        RBTreeNode<T> dataRoot = getRoot();
        while (dataRoot != null) {
            int cmp = dataRoot.getValue().compareTo(value);
            if (cmp < 0) {
                dataRoot = dataRoot.getRight();
            } else if (cmp > 0) {
                dataRoot = dataRoot.getLeft();
            } else {
                return dataRoot.getValue();
            }
        }
        return null;
    }

    /**
     * remove the node by give value,if this value not exists in tree return null
     *
     * @param value include search key
     * @return the value contain in the removed node
     */
    public T remove(T value) {
        RBTreeNode<T> dataRoot = getRoot();
        RBTreeNode<T> parent = root;

        while (dataRoot != null) {
            int cmp = dataRoot.getValue().compareTo(value);
            if (cmp < 0) {
                parent = dataRoot;
                dataRoot = dataRoot.getRight();
            } else if (cmp > 0) {
                parent = dataRoot;
                dataRoot = dataRoot.getLeft();
            } else {
                if (dataRoot.getRight() != null) {
                    RBTreeNode<T> min = removeMin(dataRoot.getRight());
                    //x used for fix color balance
                    RBTreeNode<T> x = min.getRight() == null ? min.getParent() : min.getRight();
                    boolean isParent = min.getRight() == null;

                    min.setLeft(dataRoot.getLeft());
                    setParent(dataRoot.getLeft(), min);
                    if (parent.getLeft() == dataRoot) {
                        parent.setLeft(min);
                    } else {
                        parent.setRight(min);
                    }
                    setParent(min, parent);

                    boolean curMinIsBlack = min.isBlack();
                    //inherit dataRoot's color
                    min.setRed(dataRoot.isRed());

                    if (min != dataRoot.getRight()) {
                        min.setRight(dataRoot.getRight());
                        setParent(dataRoot.getRight(), min);
                    }
                    //remove a black node,need fix color
                    if (curMinIsBlack) {
                        if (min != dataRoot.getRight()) {
                            fixRemove(x, isParent);
                        } else if (min.getRight() != null) {
                            fixRemove(min.getRight(), false);
                        } else {
                            fixRemove(min, true);
                        }
                    }
                } else {
                    setParent(dataRoot.getLeft(), parent);
                    if (parent.getLeft() == dataRoot) {
                        parent.setLeft(dataRoot.getLeft());
                    } else {
                        parent.setRight(dataRoot.getLeft());
                    }
                    //current node is black and tree is not empty
                    if (dataRoot.isBlack() && !(root.getLeft() == null)) {
                        RBTreeNode<T> x = dataRoot.getLeft() == null
                                ? parent : dataRoot.getLeft();
                        boolean isParent = dataRoot.getLeft() == null;
                        fixRemove(x, isParent);
                    }
                }
                setParent(dataRoot, null);
                dataRoot.setLeft(null);
                dataRoot.setRight(null);
                if (getRoot() != null) {
                    getRoot().setRed(false);
                    getRoot().setParent(null);
                }
                size.decrementAndGet();
                return dataRoot.getValue();
            }
        }
        return null;
    }

    /**
     * fix remove action
     *
     * @param node
     * @param isParent
     */
    private void fixRemove(RBTreeNode<T> node, boolean isParent) {
        RBTreeNode<T> cur = isParent ? null : node;
        boolean isRed = isParent ? false : node.isRed();
        RBTreeNode<T> parent = isParent ? node : node.getParent();

        while (!isRed && !isRoot(cur)) {
            RBTreeNode<T> sibling = getSibling(cur, parent);
            //sibling is not null,due to before remove tree color is balance

            //if cur is a left node
            boolean isLeft = parent.getRight() == sibling;
            if (sibling.isRed() && !isLeft) {//case 1
                //cur in right
                parent.makeRed();
                sibling.makeBlack();
                rotateRight(parent);
            } else if (sibling.isRed() && isLeft) {
                //cur in left
                parent.makeRed();
                sibling.makeBlack();
                rotateLeft(parent);
            } else if (isBlack(sibling.getLeft()) && isBlack(sibling.getRight())) {//case 2
                sibling.makeRed();
                cur = parent;
                isRed = cur.isRed();
                parent = parent.getParent();
            } else if (isLeft && !isBlack(sibling.getLeft())
                    && isBlack(sibling.getRight())) {//case 3
                sibling.makeRed();
                sibling.getLeft().makeBlack();
                rotateRight(sibling);
            } else if (!isLeft && !isBlack(sibling.getRight())
                    && isBlack(sibling.getLeft())) {
                sibling.makeRed();
                sibling.getRight().makeBlack();
                rotateLeft(sibling);
            } else if (isLeft && !isBlack(sibling.getRight())) {//case 4
                sibling.setRed(parent.isRed());
                parent.makeBlack();
                sibling.getRight().makeBlack();
                rotateLeft(parent);
                cur = getRoot();
            } else if (!isLeft && !isBlack(sibling.getLeft())) {
                sibling.setRed(parent.isRed());
                parent.makeBlack();
                sibling.getLeft().makeBlack();
                rotateRight(parent);
                cur = getRoot();
            }
        }
        if (isRed) {
            cur.makeBlack();
        }
        if (getRoot() != null) {
            getRoot().setRed(false);
            getRoot().setParent(null);
        }

    }

    //get sibling node
    private RBTreeNode<T> getSibling(RBTreeNode<T> node, RBTreeNode<T> parent) {
        parent = node == null ? parent : node.getParent();
        if (node == null) {
            return parent.getLeft() == null ? parent.getRight() : parent.getLeft();
        }
        if (node == parent.getLeft()) {
            return parent.getRight();
        } else {
            return parent.getLeft();
        }
    }

    private boolean isBlack(RBTreeNode<T> node) {
        return node == null || node.isBlack();
    }

    private boolean isRoot(RBTreeNode<T> node) {
        return root.getLeft() == node && node.getParent() == null;
    }

    /**
     * find the successor node
     *
     * @param node current node's right node
     * @return
     */
    private RBTreeNode<T> removeMin(RBTreeNode<T> node) {
        //find the min node
        RBTreeNode<T> parent = node;
        while (node != null && node.getLeft() != null) {
            parent = node;
            node = node.getLeft();
        }
        //remove min node
        if (parent == node) {
            return node;
        }

        parent.setLeft(node.getRight());
        setParent(node.getRight(), parent);

        //don't remove right pointer,it is used for fixed color balance
        //node.setRight(null);
        return node;
    }

    private T addNode(RBTreeNode<T> node) {
        node.setLeft(null);
        node.setRight(null);
        node.setRed(true);
        setParent(node, null);
        if (root.getLeft() == null) {
            root.setLeft(node);
            //root node is black
            node.setRed(false);
            size.incrementAndGet();
        } else {
            RBTreeNode<T> x = findParentNode(node);
            int cmp = x.getValue().compareTo(node.getValue());

            if (this.overrideMode && cmp == 0) {
                T v = x.getValue();
                x.setValue(node.getValue());
                return v;
            } else if (cmp == 0) {
                //value exists,ignore this node
                return x.getValue();
            }

            setParent(node, x);

            if (cmp > 0) {
                x.setLeft(node);
            } else {
                x.setRight(node);
            }

            fixInsert(node);
            size.incrementAndGet();
        }
        return null;
    }

    /**
     * find the parent node to hold node x,if parent value equals x.value return parent.
     *
     * @param x
     * @return
     */
    private RBTreeNode<T> findParentNode(RBTreeNode<T> x) {
        RBTreeNode<T> dataRoot = getRoot();
        RBTreeNode<T> child = dataRoot;

        while (child != null) {
            int cmp = child.getValue().compareTo(x.getValue());
            if (cmp == 0) {
                return child;
            }
            if (cmp > 0) {
                dataRoot = child;
                child = child.getLeft();
            } else if (cmp < 0) {
                dataRoot = child;
                child = child.getRight();
            }
        }
        return dataRoot;
    }

    /**
     * red black tree insert fix.
     *
     * @param x
     */
    private void fixInsert(RBTreeNode<T> x) {
        RBTreeNode<T> parent = x.getParent();

        while (parent != null && parent.isRed()) {
            RBTreeNode<T> uncle = getUncle(x);
            if (uncle == null) {//need to rotate
                RBTreeNode<T> ancestor = parent.getParent();
                //ancestor is not null due to before before add,tree color is balance
                if (parent == ancestor.getLeft()) {
                    boolean isRight = x == parent.getRight();
                    if (isRight) {
                        rotateLeft(parent);
                    }
                    rotateRight(ancestor);

                    if (isRight) {
                        x.setRed(false);
                        parent = null;//end loop
                    } else {
                        parent.setRed(false);
                    }
                    ancestor.setRed(true);
                } else {
                    boolean isLeft = x == parent.getLeft();
                    if (isLeft) {
                        rotateRight(parent);
                    }
                    rotateLeft(ancestor);

                    if (isLeft) {
                        x.setRed(false);
                        parent = null;//end loop
                    } else {
                        parent.setRed(false);
                    }
                    ancestor.setRed(true);
                }
            } else {//uncle is red
                parent.setRed(false);
                uncle.setRed(false);
                parent.getParent().setRed(true);
                x = parent.getParent();
                parent = x.getParent();
            }
        }
        getRoot().makeBlack();
        getRoot().setParent(null);
    }

    /**
     * get uncle node
     *
     * @param node
     * @return
     */
    private RBTreeNode<T> getUncle(RBTreeNode<T> node) {
        RBTreeNode<T> parent = node.getParent();
        RBTreeNode<T> ancestor = parent.getParent();
        if (ancestor == null) {
            return null;
        }
        if (parent == ancestor.getLeft()) {
            return ancestor.getRight();
        } else {
            return ancestor.getLeft();
        }
    }

    private void rotateLeft(RBTreeNode<T> node) {
        RBTreeNode<T> right = node.getRight();
        if (right == null) {
            throw new IllegalStateException("right node is null");
        }
        RBTreeNode<T> parent = node.getParent();
        node.setRight(right.getLeft());
        setParent(right.getLeft(), node);

        right.setLeft(node);
        setParent(node, right);

        if (parent == null) {//node pointer to root
            //right  raise to root node
            root.setLeft(right);
            setParent(right, null);
        } else {
            if (parent.getLeft() == node) {
                parent.setLeft(right);
            } else {
                parent.setRight(right);
            }
            //right.setParent(parent);
            setParent(right, parent);
        }
    }

    private void rotateRight(RBTreeNode<T> node) {
        RBTreeNode<T> left = node.getLeft();
        if (left == null) {
            throw new IllegalStateException("left node is null");
        }
        RBTreeNode<T> parent = node.getParent();
        node.setLeft(left.getRight());
        setParent(left.getRight(), node);

        left.setRight(node);
        setParent(node, left);

        if (parent == null) {
            root.setLeft(left);
            setParent(left, null);
        } else {
            if (parent.getLeft() == node) {
                parent.setLeft(left);
            } else {
                parent.setRight(left);
            }
            setParent(left, parent);
        }
    }
    
    private void setParent(RBTreeNode<T> node, RBTreeNode<T> parent) {
        if (node != null) {
            node.setParent(parent);
            if (parent == root) {
                node.setParent(null);
            }
        }
    }

    /**
     * debug method,it used print the given node and its children nodes,
     * every layer output in one line
     *
     * @param root
     */
    public void printTree(RBTreeNode<T> root) {
        java.util.LinkedListT>> queue = new java.util.LinkedListT>>();
        java.util.LinkedListT>> queue2 = new java.util.LinkedListT>>();
        if (root == null) {
            return;
        }
        queue.add(root);
        boolean firstQueue = true;

        while (!queue.isEmpty() || !queue2.isEmpty()) {
            java.util.LinkedListT>> q = firstQueue ? queue : queue2;
            RBTreeNode<T> n = q.poll();

            if (n != null) {
                String pos = n.getParent() == null ? "" : (n == n.getParent().getLeft()
                        ? " LE" : " RI");
                String pstr = n.getParent() == null ? "" : n.getParent().toString();
                String cstr = n.isRed() ? "R" : "B";
                cstr = n.getParent() == null ? cstr : cstr + " ";
                System.out.print(n + "(" + (cstr) + pstr + (pos) + ")" + "\t");
                if (n.getLeft() != null) {
                    (firstQueue ? queue2 : queue).add(n.getLeft());
                }
                if (n.getRight() != null) {
                    (firstQueue ? queue2 : queue).add(n.getRight());
                }
            } else {
                System.out.println();
                firstQueue = !firstQueue;
            }
        }
    }
}

四丶参看文章

数据结构和算法（十）：二叉树

红黑树深入剖析及Java实现

漫画：什么是红黑树？

写在最后微信扫码提问