Python 搜索、排序、复杂度分析
概述
算法是计算机程序的一个基本的构建模块。评价算法质量的最基本的标准是正确性,另一个重要的标准是运行时间性能。当在一台真实、资源有限的计算机上运行一个算法的时候,经济性的考虑就有了用武之地,这样一个过程会消耗两种资源:处理时间和空间或内存。
统计指令
用于估算算法性能的另一种技术是统计对不同的问题规模所要执行的指令的数目。不管算法在什么平台上运行,这个统计数字对于算法所要执行的抽象的工作量给出了一个很好的预计。然而要记住,当统计指令的时候,所统计的是用于编写算法的较高级代码中的指令数目,而不是执行机器语言的程序中的指令数目。
当以这种方式分析算法的时候,你需要区分两种指令:
(1)不管问题规模多大,都执行相同次数的指令
(2)根据问题的规模,执行不同次数的指令
现在,我们先忽略第一类指令,因为它们的影响并不显著,第二类指令通常在循环或递归函数中可以找到。
复杂度分析
复杂度的阶
大O表示法
一个算法几乎不太可能只是严格执行等于n、n^2或k^n的那么多次的操作,算法通常在循环体内、循环体之前或之后还要执行其他的工作。例如,我们说算法执行2n+3或2n^2操作,可能会更加精确。
一个算法的总工作量,通常是多项式中的数项之和,当用多项式来表示工作量的时候,有一个项是主项,随着n变得越来越大,主项也变得很大,以至于你可以忽略其他的项所表示的工作量。例如,在多项式(1/2)n^2-(1/2)n中,我们主要关注平方项(1/2)n^2,实际上忽略掉线性项(1/2)n,还可以删除掉系数1/2,因为(1/2)n^2和n^2之间的差别不会随着n的增加而改变。这种类型的分析有时候叫做渐进分析(asymptotic analysis)。
搜索算法
搜索最小值
Python的min函数返回列表中的最小的项。为了研究这个算法的复杂度,我们开发了一个替代的版本,它返回了最小项的索引。这个算法假设列表不为空,并且其中的项的顺序是任意的,该算法首先将列表中的第1个位置当作最小项,然后,向右搜索以找到一个更小的项,如果找到了,将最小项的位置重新设置为当前位置,当这个算法到达列表末尾的时候,它就返回最小项的位置。
class indexOfMin():
def indexOfMin(self,lyst):
"""Return the index of the minmum item."""
minIndex = 0
currentIndex = 1
while currentIndex < len(lyst):
if lyst[currentIndex] < lyst[minIndex]:
minIndex = currentIndex
currentIndex += 1
return minIndex
if __name__ == "__main__":
a = indexOfMin()
lyst = [3,5,7,1,9,10]
print(a.indexOfMin(lyst))对于大小为n的列表,该算法必须进行n-1次比较,因此,算法的复杂度为O(n)。
顺序搜索一个列表
Python的in运算符作为list类中名为__contains__的一个方法而实现。该方法在列表(任意排列的项)中搜索一个特定的项(叫做目标项)。在这样的一个列表中搜索一个目标项的唯一的方法是,从第1个位置的项开始,将其与目标项进行比较,如果这两个项相等,该方法返回一个True。否则,该方法移动到下一个位置并且将其项与目标项进行比较。如果该方法到达了最后一个位置,却仍然没有找到目标项,它就返回False。这种搜索叫做顺序搜索(sequential search)或线性搜索(linear search)。一个更为有用的顺序搜索函数,应该返回它所找到的目标项的索引,或者如果没有找到目标项的话,返回-1。
class Search():
def sequentialSearch(self,target,lyst):
"""Returns the position of the target item if found, or -1 otherwise."""
position = 0
while position < len(lyst):
if target == lyst[position]:
return position
position += 1
return -1
if __name__ == '__main__':
a = Search()
target = 3
lyst = [2,4,5,1,3,7]
print(a.sequentialSearch(target,lyst))最好情况、最坏情况和平均情况的性能
有些算法的性能取决于所处数据的放置方式。顺序搜索算法在查找一个目标项的时候,在列表的开头处所做的工作比在列表的末尾所做的工作要少。对于这样的算法,我们可以确定其最好情况的性能、最坏情况的性能和平均情况的性能。通常一般考虑的是最坏情况的性能和平均情况的性能。
顺序搜索的分析要考虑如下3种情况:
(1)在最坏情况下,目标项位于列表的末尾,或者根本就不在列表之中。那么,算法必须访问每一个项,并且对大小为n的列表要执行n次迭代。因此,顺序搜索的最坏情况的复杂度为O(n)。
(2)在最好的情况下,算法只进行了1次迭代就在第1个位置找到目标项,复杂度为O(1)。
(3)要确定平均情况,把在每一个可能的位置找到目标项所需的迭代次数相加,并且总和除以n。因此,算法执行了(n+1)/2次迭代,对于很大的n,常数因子2的作用并不大,因此,平均情况下的复杂度仍然为O(n)。
显然,顺序搜索的最好情况的性能是很少见的,而平均情况和最坏情况的性能则基本相同。
有序列表的二叉搜索
对于那些没有按照特定的顺序排列的数据,顺序搜索是必要的。当搜索经过排序的数据的时候,可以使用二叉搜索(又称为二分搜索)。
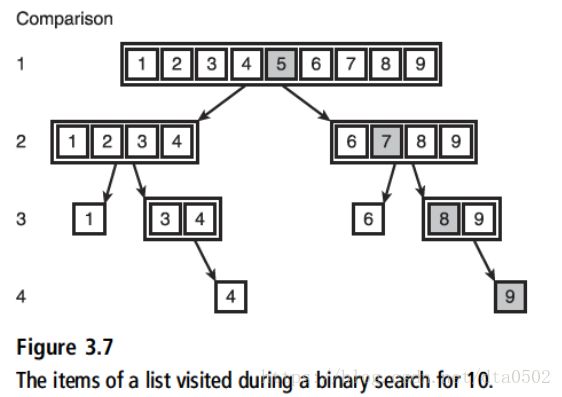
现在来考虑Python实现二叉搜索的一个示例。首先,假设列表中的项都是按照升序排列的,搜索算法直接找到列表的中间位置,并且将该位置的项和目标项进行比较。如果它们是一致的,算法返回该位置。否则,如果目标项小于当前项,算法搜索列表中间位置以前的部分。反之,搜索中间以后的部分。
def binarySearch(target, lyst, profiler):
"""Returns the position of the target item if found,
or -1 otherwise."""
left = 0
right = len(lyst) - 1
while left <= right:
profiler.comparison()
midpoint = (left + right) // 2
if target == lyst[midpoint]:
return midpoint
elif target < lyst[midpoint]:
right = midpoint - 1
else:
left = midpoint + 1
return -1在最坏的情况下,循环要运行列表的大小除以2直到得到的商为1的次数,对于大小为n的列表,实际上执行了n/2/2.../2的连续除法,直到结果为1。假设k是用n除以2的次数,要求解k,让n/(2^k)=1就行了,那么n=2^k,k=log2n,因此,二叉搜索的最坏情况的复杂度为O(log2n)。
比较数据项
二叉搜索和搜索最小项,都是假设列表中的项是可以相互比较的。在Python中,这意味着这些项具有相同的类型,并且它们都识别比较运算符==、<和>。几个内建的Python类型的对象,例如数字、字符串和列表,都可以使用这些运算符来比较。
为了允许算法对一个新对象的类使用比较运算符==、<和>,程序员应该在该类中定义__eq__、__lt__和__gt__方法。__lt__方法的方法头如下所示:
def __lt__(self,other):如果self小于other,该方法返回True,否则,它返回False。比较对象的标准,取决于它们内部的结构,以及应该以何种方式对其排序。
例如,SavingAccount对象可能包含3个数据字段,一个用于名称,一个用于PIN,还有一个用余额。假设账户应该按照名称的字母顺序来排序,那么,需要对__lt__方法按照如下的方式来实现:
class SavingAccount(object):
"""This class represents a saving account with the owner's name, PIN, and balance."""
def __init__(self,name,pin,balance = 0.0):
self._name = name
self._pin = pin
self._balance = balance
def __lt__(self,other):
return self._name < other._name注意:__lt__方法对两个账户对象的_name字段调用了<运算符(名称是字符串),并且字符串类型已经包含了一个__lt__方法。当对字符串应用<运算符的时候,Python自动运行__lt__方法。就像是在调用str函数时运行str方法一样。
基本排序算法
这里介绍的几个算法很容易编写,但是效率不高,下一节介绍的算法都很难编写,但是更为高效(这是一种常见的取舍)。每个Python排序函数都是在整数的一个列表上进行操作的,并且都会使用一个swap函数来交换列表中的两项的位置。
swap函数的代码如下:
def swap(lyst,i,j):
"""Exchanges the items at position i and j."""
temp = lyst[i]
lyst[i] = lyst[j]
lyst[j] = temp选择排序
最简单的策略就是搜索整个列表,找到最小项的位置。如果该位置不是列表的第1个位置,算法就会交换在这两个位置的项,然后,算法回到第2个位置并且重复这个过程,如果必要的话,将最小项和第2个位置的项进行交换。当算法到达整个过程的最后一个位置,列表就是排序好的了。这个算法叫做选择排序(selection sort)。
def selectionSort(lyst):
i = 0
while i < len(lyst) - 1:
minIndex = 1
j = i + 1
while j < len(lyst):
if lyst[j] < lyst[minIndex]:
minIndex = j
j += 1
if minIndex != i:
swap(lyst,minIndex,i)
i += 1这个函数包含了一个嵌套的循环。总的比较次数为(1/2)(n^2)-(1/2)n,对于较大的n,我们可以选择影响很大的项,而忽略常数项。因此,选择排序在各种情况下的复杂度为O(n^2)。
冒泡排序
另一种排序方法相对容易理解和编码,它叫做冒泡排序(bubble sort)。其策略是从列表的开头处开始,并且比较一对数据项,直到移动到列表的末尾,每当成对的两项之间的顺序不正确的时候,算法就交换其位置。这个过程的效果就是将最大的项以冒泡的方法排到列表的末尾。然后,算法从列表开头到倒数第2个列表项重复这一个过程。依次类推,直到该算法从列表的最后一项开始执行。此时,列表是已经排序好的。
def bubbleSort(lyst):
n = len(lyst)
while n > 1:
i = 1
while i < n:
if lyst[i] < lyst[i-1]:
swap(lyst,i,i-1)
i += 1
n -= 1和选择排序一样,冒泡排序也有一个嵌套的循环,对于大小为n的列表,内部的循环执行(1/2)(n^2)-(1/2)n次,因此,冒泡排序的复杂度是O(n^2)。
插入排序
(1)在第i轮通过列表的时候(其中i的范围从1到n-1),第i个项应该插入到列表的前i个项之中的正确位置。
(2)在第i轮之后,前i个项应该是排好序的。
(3)这个过程类似于人们排列手中的扑克牌的顺序,也就是说,如果你按照顺序放好了前i-1张牌,抓取了第i张牌,并且将其与手中的这些牌进行比较,直到找到其合适的位置。
(4)插入排序包括两个循环。外围的循环遍历从1到n-1的位置。对于这个循环中的每一个位置i,我们都保存该项并且从位置i-1开始内部循环。
def insertSort(lyst):
i = 1
while i < len(lyst):
itemInsert = lyst[i]
j = i - 1
while j >= 1:
if itemToInsert < lyst[j]:
lyst[j + 1] = lyst[j]
j -= 1
else:
break
lyst[j + 1] = itemToInsert
i += 1
插入排序的最坏情况下的复杂度是O(n^2)。列表中排好序的项越多,插入排序的效果越好。在最好情况下,列表本身是有序的,那么插入排序的复杂度是线性的。然而,在平均情况下,插入排序的复杂度仍然是二次方阶的。
更快的排序
到目前为止,我们介绍的3种排序算法都拥有O(n^2)的运行时间。然而,我们可以利用一些复杂度为O(nlogn)的更好的算法。这些更好的算法都采用了分而治之(divide-and-conquer)的策略,也就是说,每个算法都找到了一种方法,将列表分解为更小的子列表,随后,这些子列表再递归的排序。理想情况下,如果这些子列表的复杂度为log(n),而重新排列每一个子列表中的数据所需的工作量为n,那么,这样的排序算法总的复杂度就是O(nlogn)。
快速排序
快速排序所使用的策略可以概括如下:
(1)首先,从列表的中点位置选取一项。这一项叫作基准点。
(2)将列表中的项分区,以便小于基准点的所有项都移动到基准点的左边,而剩下的项都移动到基准点的右边。根据相关的实际项,基准点自身的最终位置也是变化的。但是,不管基准点最终位于何处,这个位置都是它在完全排序的列表中的最终位置。
(3)分而治之。对于在基准点分割列表而形成的子列表,递归地重复应用该过程。一个子列表包含了基准点左边的所有的项(现在是较小的项),另一个子列表包含了基准点右边的所有的项(现在是较大的项)。
(4)每次遇到小于2个项的一个子列表,就结束这个过程。
1.分割
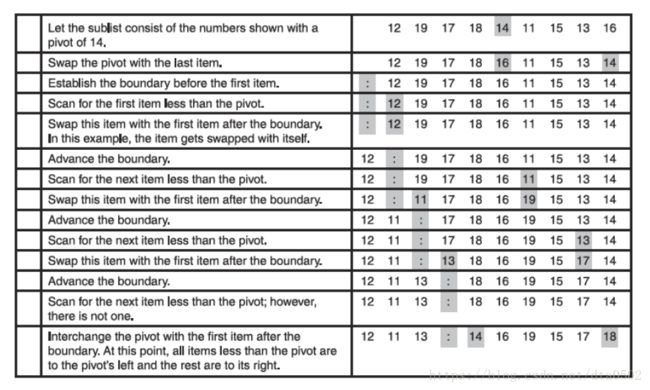
从程序员的角度来看,该算法最复杂的部分就是对子列表中的项进行分割的操作。步骤如下:
(1)将基准点和子列表中的最后一项交换。
(2)在已知小于基准点的项和剩余的项之间建立一个边界。一开始,这个边界就放在第一项之前。
(3)从子列表的第一项开始扫描整个子列表,每次遇到小于基准点的项,就将其与边界之后的第一项进行交换,并且边界向后移动。
(4)将基准点和边界之后的第一项进行交换,从而完成这个过程。
例子:
2.快速排序的复杂度分析
在第1次分割操作中,从列表头部到其尾部扫描了所有的项。因此,这个操作过程的工作量和列表的长度n成正比。
在这次分割之后的工作量,和左边的子列表的长度加上右边的子列表的长度(加在一起是n-1)成正比。当再次分割这些子列表的时候,有了4个子列表,它们组合在一起的长度近似为n,因此,组合的工作量还是和n成正比的。随着将列表分割为更多的子列表,总的工作量还是和n成正比。
然后我们需要确定对列表分割多少次。如果每一次新的子列表之间的分割线都尽可能地靠近当前子列表的中央,大概经过log2n步之后会得到一个单个的元素。因此,这个算法在最好的情况下的性能为O(nlog2n)。
对于最坏的情况,考虑一个列表已经排好序的情况。如果所选择的基准点元素是第1个元素,那么在第1次分割的时候,基准点的右边有n-1个元素,在第2次分割的时候,基准点的右边有n-2个元素,依次类推,因此,在最坏的情况下,快速排序算法的性能是O(n^2)。
如果将快速排序实现为一个递归算法,你的分析还必须考虑到调用栈所使用的内存。每一次递归调用都需要一个固定大小的内存用于栈,并且每一次分割之后有两次递归调用。因此,在最好的情况下,内存使用是O(log2n),在最坏的情况下,内存使用是O(n)。
3.快速排序的实现
快速排序使用递归算法更容易编码。
def quicksort(lyst):
quicksortHelper(lyst, 0, len(lyst) - 1)
def quicksortHelper(lyst, left, right):
if left < right:
pivotLocation = partition(lyst, left, right)
quicksortHelper(lyst, left, pivotLocation - 1)
quicksortHelper(lyst, pivotLocation + 1, right)
def partition(lyst, left, right):
# Find the pivot and exchange it with the last item
middle = (left + right) // 2
pivot = lyst[middle]
lyst[middle] = lyst[right]
lyst[right] = pivot
# Set boundary point to first position
boundary = left
# Move items less than pivot to the left
for index in range(left, right):
if lyst[index] < pivot:
swap(lyst, index, boundary)
boundary += 1
# Exchange the pivot item and the boundary item
swap (lyst, right, boundary)
return boundary
def swap(lyst, i, j):
"""Exchanges the items at positions i and j."""
# You could say lyst[i], lyst[j] = lyst[j], lyst[i]
# but the following code shows what is really going on
temp = lyst[i]
lyst[i] = lyst[j]
lyst[j] = temp
import random
def main(size = 20, sort = quicksort):
lyst = []
for count in range(size):
lyst.append(random.randint(1, size + 1))
print(lyst)
sort(lyst)
print(lyst)
if __name__ == "__main__":
main() 合并排序
另一种名为合并排序(merge sort,又称为归并排序)的算法利用了递归、分而治之的策略来突破O(n^2)的障碍。如下是该算法的一个非正式的概述:
(1)计算一个列表的中间位置,并且递归地排序其左边和右边的子列表(分而治之)。
(2)将两个排好序的子列表重新合并为单个的排好序的列表。
(3)当子列表不再能够划分的时候,停止这个过程。
有3个Python函数在这个顶层的设计策略中协作:
(1)mergeSort——用户调用的函数。
(2)mergeSortHelper——一个辅助函数,它隐藏了递归调用所需要的额外参数。
(3)Merge——实现合并过程的一个函数。
1.实现合并过程
合并的过程使用了和列表相同大小的一个数组,这个数组名为copyBuffer,为了避免每次调用merge的时候为copyBuffer分配和释放内存的开销,只在mergeSort中分配一次该缓冲区,并且在后续将其作为一个参数传递给mergeSortHelper和merge,每次调用mergeSortHelper的时候,都需要知道它所操作的子列表的边界。这些边界通过另外的参数low和high来提供,如下是mergeSort的代码:
from arrays import Array
def mergeSort(lyst):
# lyst: list being sorted
# copyBuffer: temporary space needed during merge
copyBuffer = Array(len(lyst))
mergeSortHelper(lyst,copyBuffer,0,len(lyst)-1)在检查到至少有两项的一个子列表已经传递给它之后,mergeSortHelper函数计算了这个子列表的中点,递归地对中点以上和中点以下的部分进行排序,并且调用merge来合并结果。如下是mergeSortHelper的代码:
def mergeSortHelper(lyst,copyBuffer,low,high):
# lyst: list being sorted
# copyBuffer: temp space needed during merge
# low,high : bounds of sublist
# middle: midpoint of sublist
if low < high:
middle = (low+high)//2
mergeSortHelper(lyst,copyBuffer,low,middle)
mergeSortHelper(lyst,copyBuffer,middle+1,high)
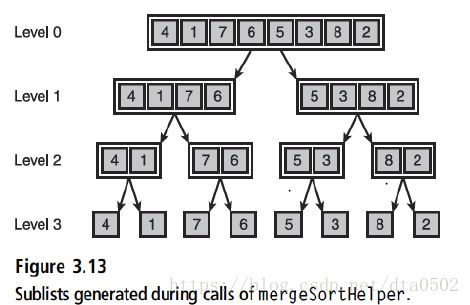
merge(lyst,copyBuffer,low,middle,high)下图展示了在对拥有8项的一个列表开始递归调用mergeSortHelper的过程中所生成的子列表。注意,在这个例子中,子列表在每一个层级都是平均划分的,在第k层,有2^k个子列表需要合并。如果最初列表的长度不是2的幂,那么,无法在每一个层级都做到完全平均的划分,并且最后的层级将不会拥有足够的子列表。
最后,下面是merge函数的代码:
def merge(lyst,copyBuffer,low,middle,high):
# Initialize i1 and i2 to the first items in each sublist
i1 = low
i2 = middle + 1
# Interleave items from the sublists into the copyBuffer in such a way that order is maintained.
for i in range(low,high+1):
if i1 > middle:
copyBuffer[i] = lyst[i2] # 列表1已经用完
i2 += 1
elif i2 > high:
copyBuffer[i] = lyst[i1] # 列表2已经用完
i1 += 1
elif lyst[i1] < lyst[i2]:
copyBuffer[i] = lyst[i1] # 将小的数放上去
i1 += 1
else:
copyBuffer[i] = lyst[i2] # 将小的数放上去
i2 += 1
for i in range(low,high+1):
lyst[i] = copyBuffer[i] # 排序完的copyBuffer返回给lystmerge函数将两个排好序的子列表合并到一个大的排好序的子列表中。第1个子列表在low和middle之间,第2个子列表在middle+1和high之间,这个过程包含步骤:
(1)将索引指针设置为每个子列表的第1项,这分别是low和middle+1的位置。
(2)从每个子列表的第1项开始,重复地比较各项。将较小的项从其子列表中复制到缓存中去,并且继续处理子列表中的下一项。重复这个过程,直到两个子列表中的所有项都已经复制过了。如果先到达了其中一个子列表的末尾,通过从另一个子列表复制剩余的项,从而结束这个过程。
(3)将copyBuffer中low到high之间的部分,复制回lyst对应的位置。
2.合并排序的复杂度分析
合并排序的运行时间由两条for语句主导,其中每一条都循环(high-low+1)次,结果,该函数的运行时间是O(high-low),在一个层的所有合并花费的时间是O(n)。由于mergeSortHelper在每一层都是尽可能平均地分割子列表,层级数是O(logn),并且在所有情况下,该函数的最大运行时间是O(nlogn)。
根据列表的大小,合并排序有两个空间需求,首先,在支持递归调用的调用栈上,需要O(logn)的空间,其次,复制缓存需要使用O(n)的空间。
指数算法:递归式的Fibonacci
递归实现
如果我们采用递归的Fibonacci函数来实现,调用的次数似乎比问题规模的平方增长的还要快,具体代码如下:
from counter import Counter
def fib(n, counter):
"""Count the number of calls of the Fibonacci
function."""
counter.increment()
if n < 3:
return 1
else:
return fib(n - 1, counter) + fib(n - 2, counter)
problemSize = 2
print("%12s%15s" % ("Problem Size", "Calls"))
for count in range(5):
counter = Counter()
# The start of the algorithm
fib(problemSize, counter)
# The end of the algorithm
print("%12d%15s" % (problemSize, counter))
problemSize *= 2counter函数如下:
class Counter(object):
"""Models a counter."""
# Class variable
instances = 0
#Constructor
def __init__(self):
"""Sets up the counter."""
Counter.instances += 1
self.reset()
# Mutator methods
def reset(self):
"""Sets the counter to 0."""
self._value = 0
def increment(self, amount = 1):
"""Adds amount to the counter."""
self._value += amount
def decrement(self, amount = 1):
"""Subtracts amount from the counter."""
self._value -= amount
# Accessor methods
def getValue(self):
"""Returns the counter's value."""
return self._value
def __str__(self):
"""Returns the string representation of the counter."""
return str(self._value)
def __eq__(self, other):
"""Returns True if self equals other
or False otherwise."""
if self is other: return True
if type(self) != type(other): return False
return self._value == other._valueProblem Size Calls
2 1
4 5
8 41
16 1973
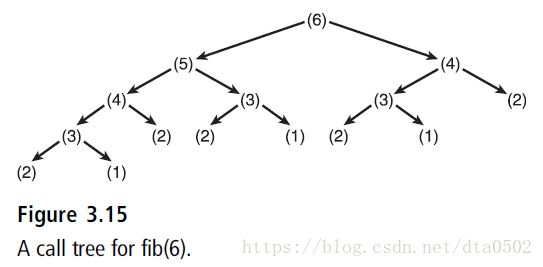
32 4356617说明工作量的快速增长的另一种方式是显示该函数针对给定的问题规模的一个调用树,下图展示了当使用递归函数来计算第6个斐波那契数的时候所用到的调用。
注意:每个填满的层级上的调用综述,都是其上一个层级的调用总数的两倍。因此,完全平衡树的递归调用次数通常是2^(n+1)-2,其中n是调用树的顶部或者根部的参数,这显然是一个指数级的O(k^n)的算法。
指数算法通常只对较小的问题规模才切合实际。尽管递归的Fibonacci在设计上很优雅,但是和使用循环按照线性时间运行的较快版本相比,它还是差很多。
此外,使用相同参数重复调用的递归函数,例如Fibonacci函数,可以通过一种叫作记忆(memoization)的技术,来使得其更有效率,根据这个技术,程序维护一张记录了函数中所使用的每一个参数的值的表。在函数递归地计算一个给定参数的值之前,它会检查这张表,看看该参数是否已经有了一个值了。如果是的,就直接返回这个值。如果没有,继续计算过程,并且随后会将参数和值添加到这个表中。
Fibonacci函数转换为一个线性算法
这种算法可以将复杂度降低到线性时间阶。
class Counter(object):
"""Tracks a count."""
def __init__(self):
self._number = 0
def increment(self):
self._number += 1
def __str__(self):
return str(self._number)
def fib(n, counter):
"""Count the number of iterations in the Fibonacci
function."""
sum = 1
first = 1
second = 1
count = 3
while count <= n:
counter.increment()
sum = first + second
first = second
second = sum
count += 1
return sum
problemSize = 2
print("%12s%15s" % ("Problem Size", "Iterations"))
for count in range(5):
counter = Counter()
# The start of the algorithm
fib(problemSize, counter)
# The end of the algorithm
print("%12d%15s" % (problemSize, counter))
problemSize *= 2Problem Size Iterations
2 0
4 2
8 6
16 14
32 30这里可以看出,该函数的新版本的性能已经提升到了线性阶。